�y�Q�l�z
�ܘQ�ŎO�����ɓ������Í����̖��H��
�a�I�ȋ����ȂƖϑz�Ȃ̐��_�Ȉ�@�Í����̕a����f�f����X��
http://2chb.net/r/hosp/1529634250/
�Í����i�T�b�|���t�@�N�g���[�����^���N���j�b�N�@���j�̂�����

�h��ӃV���c��呲���Ă��ꂾ���
��ӎ�����呲��������w��w������i�ރX�� [�]�ڋ֎~](c)2ch.net
http://2chb.net/r/hosp/1424846816/695
695 ���O�F���̖���������[] ���e���F2016/09/25(��) 22:04:25.53 ID:FzuOCpqV
�����搶
���_��
��
1
�]��
�����o�ł��A�f���炵����t�����邵�A�����ł��A�ǂ����悤���Ȃ��̂�����B
����Ȃ̂́A�����܂Ōl�̎������Ǝv���Ă܂����B
���A
������a�@�i��t�̑啔�����A�������ӎ����j�ɗ��āA���̍l���͕ς��܂����B
�Ƃ���A�C�ɐH��Ȃ���t�̔��߂�T���_�����B���A���̏�ɃS�~��u���A�ȂǁA���w�����݂������点�����Ă����t�Ƃ����̂��A�͂��߂Č��܂����B
�����o�̕ϐl�����X�݂Ă��܂������A����ȁA���w���̃C�^�Y���݂����Ȃ��Ƃ�����l�́A���܂���ł����B
��͂�A��ӎ����́A����Ȃ�ȂƎv���܂����B
2016�N09��02�� 00��21��09�b �l��▯���Ȃǖ{�l���I���ł��Ȃ����Ƃ������Ƃ����ʂ͍��ʂ̔ᔻ��Ƃ�Ȃ����A
�h��ӃV���c���i�w�͖{�l�̑I������Ȃ��B
����ȁI
�s���̖����e
>>
���͏��a�̎���ɑ�w�������ǁA�͍̂��������ʊ��������A���ꖯ�̂��߂̓���w�Z�Ƃ����C���[�W�ŊJ�ƈ�̃o�J���q�ȊO�͒N�����悤�Ƃ��炵�Ȃ������B
�펯�I�ɍl���āA���疜�Ƃ����@�O�ȋ����āA���������Ǝ҂�������҂�����o�J���̗������̂ƎU�X�l����̂��킩���čD���D��Ńh��ӈ�ɍs���������͈�l�����܂���ł����B
�{�l�ɂ͖ʂƌ������Ă͌���Ȃ�����ǁA�����炢�̔N��̐l�Ԃ́A�����炭�͂W�|�X���̓h��ӈ㑲�����ł��u���̂����Ȃ��Ɣ������Ă�A���̗����o�J���v�ƐS�̒�Ōy�̂��A�}���Ă����B
���̖{�l�ɂ͖ʂƌ������Ă͐�ɂ���Ȃ��Ƃ͌���Ȃ����ǂˁB
<<
�������̎����͗������w�����ݐi�s�`�ł��邱�Ɣ@���ɂ��߂�����������ˁB
�V���c��̎g���͗������w�o�ō����^���̐擪�ɗ����Ƃ���B
�������w�̊w�������Џ����ɂ��Ȃ�������A�M���̉͂Ȃ��ˁB�܂�A���܂Ōo���Ă��V���c��呲�������o�J�Ɖ����͐@���Ȃ��B�V���c�o�g�҂����A�������w�Ɍ��������������i����ׂ��B
�������w��t�̖Ƌ����D���I�̍����^���̐擪�ɗ��Ă悢���B
�l���������w�Ƃ��A�����Ă���M���̉͂Ȃ��B
Last but not least, three laws of Do-Teihen Medical School, currently called Gachi'Ura by its graduates.
�Ō�Ƀh��ӈ��̎O�@�����f���܂��傤�B�@�@
1: It is not the bottom medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
�h��ӃV���c��傪�����̂ł͂Ȃ��A�{�l�̓��������B
2: The graduates of Do-Teihen are so ashamed that none of them dare to mention their own alma mater�@which they have gone through.
�h��ӃV���c��呲�͒p���������āA�w�Z�����F���܌����܂���B
3: The Do-Teihen graduates are so ashamed of having bought their way into the exclusively bottom-leveled medical school
that they tend to call a genuine doctor a charlatan who elucidates their imbecility.
�h��ӓ���V���c��呲�͗������w�̕����ڂ��痠���n����\���l�Ԃ��U��҈�����������B
������R���s���[�^�Ȃ��ʼn����铪�]�ɂ͊�������B
�ԐF�̃J�����I���R�C�ƁA�F�̃J�����I���T�C�ƁA���F�̃J�����I�����W�C����B
�����A�قȂ�F�̂Q�C�̃J�����I�����o��A�Q�C�Ƃ��R�Ԗڂ̐F�ɕς��B
�Ⴆ�A�F�Ɖ��F���o���2�C�Ƃ��ԐF�ɂȂ�B
�����F�̂Q�C�̃J�����I�����o����Ă��F�͕ς��Ȃ��B
�o����d�˂āA�S�ẴJ�����I���������F�ɂȂ邱�Ƃ͉\���H
�\�Ȃ�Ή��F�ɂȂ邩�H
���͖�ƕ������������˂�
���������i��������ȃJ�X
>>6
����Ȑ��ɂȂ�ƃR���s���[�^������������Ȃ������_�l�͐������o���Ă�����Ȃ��B
�ԐF�̃J�����I���X�X�C�ƁA�F�̃J�����I���P�O�O�C�ƁA���F�̃J�����I�����P�O�P�C�̏ꍇ�͂ǂ����H
�ԐF�̃J�����I���V�V�V�C�ƁA�F�̃J�����I���W�W�W�C�ƁA���F�̃J�����I�����X�X�X�C�̏ꍇ�͂ǂ����H
���������̂��T���b�Ɠ������铪�]�����w����H�w���ɂ����ȁB
�l���悤�Ƃ����Ȃ��z�������̂������Ńh��ӃV���c���ł���̂͐\���܂ł��Ȃ��B ��₂�����B��������{����������B
�����̓A�N���o�b�g�i��ň��{�ɑ݂�������Ė�l���]�ސ�������������Ă�B
�����̂��Ƃ�������{�������l�^�Ƃ��ē����ɖ���͕ۊǂ��Ă��邾�낤�B
���Y�}�̋c���ɂ܂Ń~���V���K�[������Ă��̂����{�B
�����̋c���ɂ��u���Y�}�I�v�Ƃ�����̂����{�B
���͍��o���ق����K�ߕ����w�������āu���Y�}�I�I�v�Ƃ���Ăق������B
������v���O�����������Ȃ��B
��0 ��1 ��2�̐����������Ă���Ƃ���
Z/3�ōl������
0+1=2+2 �ԂƐ���2�ɕς��
1+2=0+0 �Ɖ�����2�ɕς��
2+0=1+1 ���ƐԂ���2�ɕς��
�ŕω��̑O��ō��v�͕ς��Ȃ�
0*13+1*15+2*17=1
13+15+17=0
0*x=1�͌����Đ������Ȃ�
�t��
0x+1y+2z=d(x+y+z)
�ƂȂ�d�����݂���Ƃ�
1x+2y+0z=(d+1)(x+y+z)
2x+0y+1z=(d+2)(x+y+z)
�ł���̂�
��ʐ������킸d=0�Ƃ��Ă悢
���Ȃ킿
0x+1y+2z=0
z=y+3n
n=0�Ȃ�
0(x+y+z)+1*0+2*0=0
�Ƃł���
n>0�Ȃ�
0(x+y)+1*0+2(3n)=0
0(x+y)+1(3n)+2*0=0
n=-m<0�Ȃ�
0(x+z)+1(3m)+2*0=0
�Ƃł���̂�
��������
0n+1(3m)+2*0=0
m>0
�Ƃ��Ă悢
n=0�Ȃ�I���Ȃ̂�n>0�Ƃ����
0(n-1)+1(3m-1)+2*2=0
0(n+3)+1(3(m-1))+2*0=0
�Ƃł���̂Ŏ���Ɍ��炵��
0(n+3m)+1*0+2*0=0
�ɂ��邱�Ƃ��\
��́A��������{�͂����Ȃ��Ă��܂����̂ł��傤���H
��҂͐��Ј��ł���15���~�قǂ̎���Ń{�[�i�X�����B
�q�ǂ���7�l��1�l���n����ԁB(��i���̒��ł��ň��Ȑ���)
���q����Ől��s���ɂȂ�A����Ƌ������オ�낤�Ƃ��Ă��鏊�Ɉږ������A���^�̏㏸��}���悤�Ƃ��鐭�{�B
�ЊQ�ō����̖����D��ꑱ���A�����̕x������Ă���ɂ��ւ�炸�\���Ȗh�Б�����Ȃ����B
�f�����b�g�����Ȃ��Ƃ킩���Ă���ɂ��ւ�炸���s���ꂽ����ł̑��ŁB
���I�̑唭���ł���iPS�זE�ɂł���A�x��(�N10���~)��ł��낤�Ƃ��鐭�{�E�����ȁB
�o�J�����̍����^�c���Ă���B
���q�������A�V���c��w�p�~�ł�����ˁH
1 ���炢�� �� 2020/01/10(��) 16:47:33.70 ID:yEOurkSc9
�����w�Ŋw���������h�� �w���̐g���m��
�@���m���x�@�{���ɂ��܂���10���ߌ�S�������A���É��s�V����̖����w�Ŋw�����������h�����ƒʕ������Ƃ������Ƃł��B
�@�����͕a�@�ɉ^��܂������A�ڂ����e�̂͂킩���Ă��܂���B
�@�x�@�͊w���̐g�����m�ۂ��ڂ����ׂĂ��܂��B
NHK NEWS WEB�@2020�N1��10�� 16��45��
https://www3.nhk.or.jp/news/html/20200110/k10012241491000.html "�ԐF�̃J�����I��13�C�ƁA�F�̃J�����I��15�C�ƁA���F�̃J�����I����17�C����B
�����A�قȂ�F��2�C�̃J�����I�����o��A2�C�Ƃ�3�Ԗڂ̐F�ɕς��B
�Ⴆ�A�F�Ɖ��F���o���2�C�Ƃ��ԐF�ɂȂ�B
�����F��2�C�̃J�����I�����o����Ă��F�͕ς��Ȃ��B
���̂Ƃ��A�S�ẴJ�����I���������F�ɂȂ邱�Ƃ͉\���H"
ct <- function(x,y){ # camelleon transformation
if(x==y)return(0)�@# ���F�Ȃ�0��Ԃ�
else return((1:3)[-c(x,y)]) # �ِF�Ȃ��R�F��Ԃ�
}
ce <- function(x){ # camelleon encounter x=c(1,2,2,3,3,3)
N=length(x)
ab=sample(N,2) # index����Q�I��
a=x[ab[1]] # index�ɑ�������x�̗v�f
b=x[ab[2]]
z=ct(a,b) # camelleon transformation
if(z!=0){�@�@�@# ���F�łȂ����
x[ab[1]]=z # ��R�̐F�ɓ���ւ���
x[ab[2]]=z
}
return(x)
}
is.uc <- function(x){ # is uniform color?
y=unique(x)
if(length(y)==1) return(y) # ��F�Ȃ炻�̐F�ԍ���Ԃ�
else return(0) # ����ȊO��0��Ԃ�
}
ca <- function(r,b,y) rep(1:3,c(r,b,y)) # camelleon array
sim <- function(r,b,y,k=1e3,verbose=FALSE){
x=ca(r,b,y) # �F�ʂ̐�����J�����I���z��`��
U=FALSE # ��F���H
i=0
while(!U){ # camelleon encounter����F�ɂȂ�܂�
# while(!U & k>0){ # camelleon encounter���ő�k��J��Ԃ�
if(verbose) cat(i,':',x,'\n') ; i=i+1 #�@�z��\��
x=ce(x)
U=is.uc(x)
# k=k-1
if(U) {
print(x)
break # �r���ň�F�Ȃ�loop����
}
}
return(U) # ��F�ɂȂ�������Ԃ�
}
sim(1,3,4) # ������]������F 1 0 1�@�䂦2�Ԃ�
replicate(10,sim(1,4,7)) # ��]������������P 1 1�䂦3�F����F�ɂȂ��
try(sim(1,2,3)) # ����s�\ �������[�v
�����𗝋l�߂łǂ��ؖ����邩�̖�肾�ȁB
�y��1�z�F����Ԃ�2020�̐����A�ǂ�2�̐��̋������قȂ�悤�ɔz�u����Ă���B
�������A���͉F����ԂɌŒ肳��Ă���Ƃ���i���]�Ȃǂ͍l���Ȃ��j�B
�e���ɂ͓V���w�҂����āA�����ƍł��߂����������ϑ����Ă���B
���̂Ƃ��A�u�ǂ̓V���w�҂ɂ��ϑ�����Ȃ������K�����݂���v�͐^���U���B
�y��2�z2021�̂Ƃ��ł͂ǂ����B
>>16
�V�~�����[�V����
rm(list=ls())
gsc <- function(N,M,cmplx=TRUE){ # M�~M�̑傫���̕��f���ʂ�N�̐���z�u
f=function(x){
ab=sample(x,2,replace=TRUE)
ifelse(cmplx,ab[1]+1i*ab[2],ab[1])}
replicate(N,f(M))
}
dista <- function(x,y) abs(x-y) # ���̋���
snest <- function(i){ # i�Ԗڂ̐��ɍł��߂�����I�т���index��Ԃ�
dis=dista(cons[i],cons) # ����0�̎��g���܂߂Ă��ׂĂ̐��Ƃ̋������o����
which(dis==min(dis[-i])) # �O�������čŏ��̒l��index��Ԃ�
}
Snest <- Vectorize(snest) # �x�N�g���Ή���
sim <- function(N,M,cmp){
cons=gsc(N,M,cmp) # constellation ����z�u
d=combn(N,2,function(z) dista(cons[z[1]],cons[z[2]])) # ���ׂĂ�2���Ԃ̋���
if(length(unique(d))==length(d)){ # ���̊Ԃ̋������قȂ邱�Ƃ��m�F
os=Snest(1:N) # os : observed star �e������ώ@���Ă��鐯��index�z���Ԃ�
all(1:N %in% os) # os �����ׂĂ̐����܂�ł��邩
}
} snest <- function(i,cons){ # ���̔z��cons��i�Ԗڂ̐��ɍł��߂�����I�т���index��Ԃ�
dis=abs(cons-cons[i]) # ����0�̎��g���܂߂Ă��ׂĂ̐��Ƃ̋������o����
which(dis==min(dis[-i])) # �O�������čŏ��̒l��index��Ԃ�
}
als <- function(N=4,M=16){ # allocate stars
cons=sample(M,N) # constellation ���𐔒���1,2,..,M��ɔz�u
d=combn(N,2,function(z) abs(cons[z[1]] - cons[z[2]])) # ���ׂĂ�2���Ԃ̋���
if(length(unique(d))==length(d)){ # ���̊Ԃ̋������قȂ邱�Ƃ��m�F
os=sapply(1:N,function(x) snest(x,cons)) # os:observed star �ώ@���Ă��鐯��index�z���Ԃ�
as=all(1:N %in% os) # all stars : os �����ׂĂ̐����܂�ł��邩
if(as) return(sort(cons)) # ���ׂĊ܂�ł���ΐ��̔z����\�[�g���ĕԂ�
}
else return(0) # ���ꋗ��������A��ώ@���������0��Ԃ�
}
# ���ׂĊώ@�����z������̔z���Ԃ��Ak��܂łɂȂ����0��Ԃ�
sim <- function(N,M,k=NULL){ # k:����ANULL�Ȃ琧���Ȃ�
AS=0 # all star observed
if(is.null(k)){ # �݂���܂ŌJ��Ԃ�
while(sum(AS)==0){
AS=als(N,M)
}
}else{
while(sum(AS)==0 & k > 0){ # ���k��
AS=als(N,M)
k=k-1
}
}
AS
}
> sim(4,16)
[1] 8 9 13 16
> sim(4,16)
[1] 3 5 11 12
> sim(6,24)
[1] 1 2 12 16 21 24
> sim(8,64)
[1] 5 6 33 36 40 42 50 55
> sim(10,128)
[1] 2 6 16 17 41 44 53 60 112 125
���P�U�̏ꍇ

> sim(16,256)
[1] 7+198i 18+ 73i 36+ 16i 36+ 59i 43+212i 61+ 12i 80+102i 103+ 86i 105+127i
[10] 115+122i 140+230i 143+235i 194+ 39i 210+228i 219+ 85i 241+235i # search nearest star from constellation
snest <- function(i,cons){ # ���̔z��cons��i�Ԗڂ̐��ɍł��߂�����I�т���index��Ԃ�
dis=abs(cons-cons[i]) # ����0�̎��g���܂߂Ă��ׂĂ̐��Ƃ̋������o����
which(dis==min(dis[-i])) # �O�������čŏ��̒l��index��Ԃ�
}
# allocate stars # ���ԋ��������ׂĈقȂ�A�S�Ċώ@����Ă��鐯�̔z���T��
als <- function(N=4,M=16){ # ������N�̐���1,2,...M�̐������ɔz�u���A�K�����Ă��邩������
consRe=sample(M,N,replace=TRUE) # constellation ���𐔒���1,2,..,M��ɔz�u
consIm=sample(M,N,replace=TRUE)
cons=complex(N)
for(i in 1:N) cons[i]=consRe[i]+1i*consIm[i]
d=combn(N,2,function(z) abs(cons[z[1]] - cons[z[2]])) # ���ׂĂ�2���Ԃ̋���
if(length(unique(d))==length(d)){ # ���̊Ԃ̋������قȂ��
os=sapply(1:N,function(x) snest(x,cons)) # os:observed star �ώ@���Ă��鐯��index�z���Ԃ�
as=all(1:N %in% os) # all stars : os �����ׂĂ̐����܂�ł��邩
if(as){
plot(cons,bty='l',pch=19,asp=1)
return(sort(cons)) # ���ׂĊ܂�ł���ΐ��̔z����\�[�g���ĕԂ�
}
}
else return(0) # ���ꋗ��������A��ώ@���������0��Ԃ�
}
# ���ׂĊώ@�����z������̔z���Ԃ��Ak��܂łɂȂ����0��Ԃ�
sim <- function(N,M,k=NULL){ # k:����ANULL�Ȃ琧���Ȃ�
AS=0 # all star observed
if(is.null(k)){ # �݂���܂ŌJ��Ԃ�
while(sum(AS)==0){
AS=als(N,M)
}
}else{
i=0
while(sum(AS)==0 & i < k){ # ���k��
AS=als(N,M)
i=i+1
}
cat('i =',i,'\n')
}
AS
}
> sim(4,16)
[1] 7+ 1i 10+ 6i 15+12i 16+ 9i
> sim(6,24)
[1] 1+ 3i 1+24i 3+18i 4+ 8i 21+ 9i 24+19i
> sim(8,64)
[1] 15+41i 21+37i 28+41i 28+49i 34+26i 44+24i 51+16i 58+18i
> sim(10,128)
[1] 1+ 41i 9+ 4i 10+ 98i 26+ 2i 30+ 51i 45+ 88i 86+ 31i 112+122i 118+124i
[10] 123+ 9i
> sim(12,256)
[1] 10+ 16i 45+ 47i 56+249i 65+227i 93+178i 128+231i 143+161i 169+ 45i 174+ 43i
[10] 176+252i 201+ 4i 232+ 25i
> sim(16,256)
[1] 2+184i 46+ 53i 76+194i 99+ 27i 125+108i 167+134i 170+ 63i 184+ 26i 184+ 66i
[10] 184+223i 189+ 21i 216+ 44i 216+236i 222+166i 240+ 40i 249+199i
# 1 �~ 1�̑傫���̕��f���ʂ�N�̐�����l���z�Ŕ��������� (1)���ԋ����s�� (2)�ŒZ���ώ@ (3)�S����ώ@�@�������̂��A�݂���܂ŌJ��Ԃ�
# search nearest star from constellation
snest <- function(i,cons){ # ���̔z��cons��i�Ԗڂ̐��ɍł��߂�����I�т���index��Ԃ�
dis=abs(cons-cons[i]) # ����0�̎��g���܂߂Ă��ׂĂ̐��Ƃ̋������o����
which(dis==min(dis[-i])) # �O�������čŏ��̒l��index��Ԃ�
}
# draw arrow from complex a to complex b ���`�o
arrow <- function(a,b,...){
arrows(Re(a),Im(a),Re(b),Im(b),...)
}
# allocate stars # (1)���ԋ����s�� (2)�ŒZ���ώ@ (3)�S����ώ@�̔z���T��
als <- function(N=16){ # ������N�̐��f���ʂɔz�u���A�K�����Ă��邩������
consRe=runif(N) # ����:��l���z[0,1]�ŗ�������
consIm=runif(N) # ����:��l���z[0,1]�ŗ�������
cons=complex(N)�@# constellation�̗e�ꕨ(���f���z��)
for(i in 1:N) cons[i]=consRe[i]+1i*consIm[i] # ���f����
d=combn(N,2,function(z) abs(cons[z[1]] - cons[z[2]])) # ���ׂĂ�2���Ԃ̋���
if(length(unique(d))==length(d)){ # (1)���ԋ����s���Ȃ��
os=sapply(1:N,function(x) snest(x,cons)) # �ŒZ��ώ@����index�z���os(observed star)�ɑ��
as=all(1:N %in% os) # (3)�S����ώ@ os �����ׂĂ̐����܂�ł��邩��as(all stars)�ɑ��
if(as){ # �S��ώ@�̏��������O���t��
plot(cons,bty='l',pch='��',asp=1) # ���`��
for(i in 1:N) arrow(cons[i],cons[os[i]],length=0.1,col='blue') # �ώ@���`��
return(sort(cons)) # ���̔z��������Ń\�[�g���ĕԂ�
}
}
else return(0) # ���ꋗ�������邩�A��ώ@���������0��Ԃ�
}
# ���ׂĊώ@�����z������̔z���Ԃ��Ak��܂łɂȂ����0��Ԃ�
sim <- function(N,k=NULL){ # k:����ANULL�Ȃ琧���Ȃ�
AS=0 # all star observed �����l
if(is.null(k)){ # k=NULL�Ȃ�݂���܂ŌJ��Ԃ�
while(sum(AS)==0){ # AS��0���z��Ȃ̂�sum�Ő��l�ɂ��Ĕ�r(max(AS)�ł���)
AS=als(N)
}
}else{
i=0
while(sum(AS)==0 & i < k){ # ���k��
AS=als(N)
i=i+1
}
cat('i =',i,'\n') # ���k��̉���ڂ̎��s�ŏ�����������
}
AS
}
sim(16)
# 
sim(15) # Endless ���ׂĂ̐����ŒZ�����̐�����ώ@����Ă���z�u�����݂���Ƃ��āA���̐��̏W����A�Ƃ���B
A����a->b b<-a�̂悤�ɑ��݊Ď�����Ă��鐯�������W����B�Ƃ���B�����ꂽ���̏W����C�ƌĂԁB
B�̗v�f��1�̐��ł�����̐��͂ǂ�������ώ@����Ă��Ȃ�����A�̑O��ɔ�����B
B�̗v�f�̐������Ƃ���Bb�l�̂�����l�ł�C�ɑ����鐯���ώ@���Ă����B�̒��Ɋώ@����Ȃ������o������B
�����A�̑O��ɔ����邩��Ab�l�͂��ׂ�B�ɑ����鐯���ώ@���Ă��邱�ƂɂȂ�B
B�ɑ����鐯�Ő��Ԃ̋������ŒZ��2�̐��͑��݊Ď����Ă��邱�ƂɂȂ�B�̑O��ɔ�����B
�䂦��B�͋�W���ł���B
The Disappearance of Bambi Woods
https://www.ama��zon.com/Disappearance-Bambi-Woods-anthology-Crime-ebook/dp/B07L159FNN/ref=sr_1_1?keywords=The+Disappearance+of+Bambi+Woods&qid=1578832618&s=books&sr=1-1
Wikipedia�ȏ�̏��͂Ȃ��Ă܂�Ȃ������B 1�`100000�܂ł̎��R���̒�����A�u�ǂ�3��I��ł���������𐬂��Ȃ�2020�̐��v���I�ׂ邱�Ƃ�����
�v���O��������100����Ă݂��B
100�ł����H�̎��ԂɌv�Z�I����Ă��B
> a
[1] 1 2 4 5 10 11 13 14 28 29 31 32 37 38 40 41 82 83 85 86 91 92 94 95 109
[26] 110 112 113 118 119 121 122 244 245 247 248 253 254 256 257 271 272 274 275 280 281 283 284 325 326
[51] 328 329 334 335 337 338 352 353 355 356 361 362 364 365 730 731 733 734 739 740 742 743 757 758 760
[76] 761 766 767 769 770 811 812 814 815 820 821 823 824 838 839 841 842 847 848 850 851 973 974 976 977
>
rm(list=ls())
p3c <- function(x){ # pick 3 numbers and check if arithmatic sequence
is.as3 <- function(x) diff(x)[1]==diff(x)[2]
is.as=function(y) is.as3(c(x[y[1]],x[y[2]],x[y[3]]))
n=length(x)
any(combn(n,3,is.as)) #
}
M=20
a=c(1,1,2)
i=1
AS=FALSE
while(length(a) < M){
a=append(a,rev(a)[1])
AS=p3c(a)
if(AS){
a=a[-length(a)]
}else{
a=append(a,i)
if(AS){
a=a[-length(a)]
}
}
i=i+1
}
a
���Ãn���h�u�b�N�̍ŐV�ł������B
���N���ʓǗ\��B���N�ʓǂ��Ă���Ɠǂނ̂��y���݁B
�O���������̉��̌����͖ʔ����Ȃ���ŎO���������̉��̌����ɍs���O�ɁA
a=��(4-4t+3t^2)/(1-t+t^2) ���������������Ă��炦�܂��H
R�̓�
> f <- expression(sqrt(4-4*t+3*t^2)/(1-t+t^2))
> D(f , 't')
0.5 * ((3 * (2 * t) - 4) * (4 - 4 * t + 3 * t^2)^-0.5)/(1 - t +
t^2) - sqrt(4 - 4 * t + 3 * t^2) * (2 * t - 1)/(1 - t + t^2)^2
>
Possible derivation:
d/dt(sqrt(4 - 4 t + 3 t^2)/(1 - t + t^2))
Use the quotient rule, d/dt(u/v) = (v ( du)/( dt) - u ( dv)/( dt))/v^2, where u = sqrt(3 t^2 - 4 t + 4) and v = t^2 - t + 1:
= (-sqrt(4 - 4 t + 3 t^2) (d/dt(1 - t + t^2)) + (1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))))/(1 - t + t^2)^2
Differentiate the sum term by term and factor out constants:
= ((1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))) - d/dt(1) - d/dt(t) + d/dt(t^2) sqrt(4 - 4 t + 3 t^2))/(1 - t + t^2)^2
The derivative of 1 is zero:
= ((1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))) - sqrt(4 - 4 t + 3 t^2) (-(d/dt(t)) + d/dt(t^2) + 0))/(1 - t + t^2)^2
Simplify the expression:
= (-sqrt(4 - 4 t + 3 t^2) (-(d/dt(t)) + d/dt(t^2)) + (1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))))/(1 - t + t^2)^2
The derivative of t is 1:
= ((1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))) - sqrt(4 - 4 t + 3 t^2) (d/dt(t^2) - 1))/(1 - t + t^2)^2
Use the power rule, d/dt(t^n) = n t^(n - 1), where n = 2.
d/dt(t^2) = 2 t:
= ((1 - t + t^2) (d/dt(sqrt(4 - 4 t + 3 t^2))) - sqrt(4 - 4 t + 3 t^2) (-1 + 2 t))/(1 - t + t^2)^2
Using the chain rule, d/dt(sqrt(3 t^2 - 4 t + 4)) = ( dsqrt(u))/( du) ( du)/( dt), where u = 3 t^2 - 4 t + 4 and d/( du)(sqrt(u)) = 1/(2 sqrt(u)):
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + (1 - t + t^2) (d/dt(4 - 4 t + 3 t^2))/(2 sqrt(3 t^2 - 4 t + 4)))/(1 - t + t^2)^2
Differentiate the sum term by term and factor out constants:
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + d/dt(4) - 4 d/dt(t) + 3 d/dt(t^2) (1 - t + t^2)/(2 sqrt(4 - 4 t + 3 t^2)))/(1 - t + t^2)^2
The derivative of 4 is zero:
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + ((1 - t + t^2) (-4 (d/dt(t)) + 3 (d/dt(t^2)) + 0))/(2 sqrt(4 - 4 t + 3 t^2)))/(1 - t + t^2)^2
Simplify the expression:
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + ((1 - t + t^2) (-4 (d/dt(t)) + 3 (d/dt(t^2))))/(2 sqrt(4 - 4 t + 3 t^2)))/(1 - t + t^2)^2
The derivative of t is 1:
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + ((1 - t + t^2) (3 (d/dt(t^2)) - 1 4))/(2 sqrt(4 - 4 t + 3 t^2)))/(1 - t + t^2)^2
Use the power rule, d/dt(t^n) = n t^(n - 1), where n = 2.
d/dt(t^2) = 2 t:
= (-(-1 + 2 t) sqrt(4 - 4 t + 3 t^2) + ((1 - t + t^2) (-4 + 3 2 t))/(2 sqrt(4 - 4 t + 3 t^2)))/(1 - t + t^2)^2
Simplify the expression:
= (((-4 + 6 t) (1 - t + t^2))/(2 sqrt(4 - 4 t + 3 t^2)) - (-1 + 2 t) sqrt(4 - 4 t + 3 t^2))/(1 - t + t^2)^2
Simplify the expression:
Answer: |
| = (2 - 7 t + 6 t^2 - 3 t^3)/((1 - t + t^2)^2 sqrt(4 - 4 t + 3 t^2))
���ʏ�ɁA�ǂ�3�_�����꒼����ɂȂ��悤��n�̓_��z�u����Ƃ��A�����̒���5�_�_�Ƃ���ʌ܊p�`�����Ȃ��Ƃ�1���݂��邽�߂�n�̍ŏ��l�����߂�B
��An=6�̂Ƃ�
�@�E�@�@�E
�@�@�E�E�@
�@�E�@�@�E
�̂悤�ɔz�u����ƁA�ǂ��ɂ��ʌ܊p�`���ł��Ȃ��̂ŁAn=6�͕s�K�B
rm(list=ls())
graphics.off()
# draw segment of complex a to complex b
seg <- function(a,b,...){
segments(Re(a),Im(a),Re(b),Im(b),...)
}
# draw text y at complex x
pt <- function(x,y=NULL,...){
text(Re(x),Im(x), ifelse(is.null(y),'+',y), ...)
}
# connect every point(vertex)
coep <- function(ij,ve){
seg(ve[ij[1]],ve[ij[2]],col='gray',lty=3)
invisible(0)
}
# �꒼����ɂ��邩�H�O��=0�Ɠ���
align <- function(xyz){ # y-y1 = m(x-x1), m=(y2-y1)/(x2-x1) ��z1�z2����������?
x=xyz[1];y=xyz[2];z=xyz[3]
(Im(z)-Im(x))*(Re(x)-Re(y)) == (Im(x)-Im(y))*(Re(z)-Re(x))
}
# ����_���O�p�`�̓����ɂ��邩�H
oup <- function(A,B){ # �O�� outer prodct
Ax=A[1];Ay=A[2];Az=A[3]
Bx=B[1];By=B[2];Bz=B[3]
c(Ay*Bz-Az*By, Az*Bx-Ax*Bz, Ax*By-Ay*Bx)
}
# ���Ȃ̂� Z���̒l�̐����݂̂��K�v
opc <- function(a,b){ # outer product on complex plane
Re(a)*Im(b)-Im(a)*Re(b)
}
align <- function(ABC){ # �x�N�g��AB�ƃx�N�g��AC�̊O�ς�0�Ȃ�3�_�͒�����ɂ���
opc(ABC[2]-ABC[1],ABC[3]-ABC[1])==0
}
in3 <- function(P,A,B,C){ # is P inside triangle ABC?
sum(opc(B-A,P-A)>0,opc(C-B,P-B)>0,opc(P-A,C-A)>0)%%3==0
#�@�E�˂��O�ς̕�����Z���őS�Đ����S�ĕ����ŎO�p�`�̓����Ɗm�F
}
concave <- function(ve){
for(i in 2:5){
tri=ve[-i] # i�Ԗڂ�P�Ƃ���
tm=matrix(tri[combn(4,3)],nrow=3) # triangl matrix for ABC (4���)
for(j in 1:4){
inside=in3(ve[i],tm[1,j],tm[2,j],tm[3,j]) # ���_��ABC�̓����ɂ��邩�H
if(inside) return(TRUE)
}
}
return(FALSE)
}
sim <- function(draw=TRUE){
ve=c(0,runif(4)+runif(4)*1i) # vertex ��l���z�����Œ��_��
v3=matrix(ve[combn(5,3)],nrow=3) # 3�_�̑g�ݍ��킹10�ʂ�
for(i in 1:10){
aln=align(v3[,i]) # �����ꂩ��3�_��������ɂ����
if(aln) return(NA) # NA��Ԃ�
}
if(draw){
plot(ve,xlim=c(0,1),ylim=c(0,1),bty='l',pch=as.character(1:5), cex=0.75,
axes=TRUE, ann=FALSE,asp=1)
combn(5,2,function(x) coep(x,ve))}
if(concave(ve)) return(FALSE) # ���Ȃ��FALSE
else�@return(TRUE) # �ʂȂ�TRUE��Ԃ�
}
sim()
k=1e6
cvx5=replicate(k,sim(draw=F))
sum(is.na(cvx5))
> mean(cvx5)
[1] 0.270576
>>32
n=7���s�K�ȗ���p�\�R���ŏo���Ă݂��B

���f���ʂł̂V�̍��W��
[1] 0.0000000+0.0000000i 0.8328849+0.3868275i 0.9219985+0.4125254i 0.8392956+0.9398254i
[5] 0.8249211+0.8054688i 0.7128166+0.5062512i 0.3850924+0.3886969i >>32
�������ɕς��Ă݂��B
�P�O�O���������Ă���`���p���W�[�Ɠq��������
�ǂɌ������Ėڂ��ނ��Ė���ׂɃ_�[�c����U�{������B
�E�@�@�E
�@�@�E�E�@
�@�E�@�@�E
�̔z�u�̂悤�ɁA�ǂ̂T�_��I��ł��ʌ܊p�`���ł��Ȃ��ꍇ�̓`���p���W�[�̏����ł��Ȃ��͊|������S�Ď����B
�ʌ܊p�`���ł���T�_��I�ׂ�z�u�Ȃ�`���p���W�[����P�O�O���~�����炦��B
�|������������܂łȂ�L���ȓq���Ƃ����邩�H sim.n <- function(n=7,draw=TRUE,concave.draw=TRUE){
ve=c(0,runif(n-1)+runif(n-1)*1i) # vertex ��l���z�����Œ��_��n����������
v3=matrix(ve[combn(n,3)],nrow=3) # 3�_�̑g�ݍ��킹
m=choose(n,3) # m�ʂ��
for(i in 1:n){
aln=align(v3[,i]) # �����ꂩ��3�_��������ɂ����
if(aln) return(NA) # NA��Ԃ�
}
m5=choose(n,5) # n����T�I�ԑg�ݍ��킹
v5=matrix(ve[combn(n,5)],nrow=5) # ��5�sm5����쐬
convx=FALSE # �ʂ�?��flag
for(i in 1:m5){
ver5=v5[,i] # i��ڂ��ʂ����ׂ�
convx=convex(ver5)
if(convx){ # �ʂȂ��
if(draw){ # �`�悵��
plot(ver5,xlim=c(0,1),ylim=c(0,1),bty='l',pch=19,
axes=TRUE, ann=FALSE,asp=1)
combn(5,2,function(x) coep(x,ver5))
points(ve) # n�_�`��
}
break �@�@�@�@�@�@�@�@ # for loop���甲����
}
}
if(!convx & concave.draw){ # �ʂ������ꍇ
print(ve) # ���_��\�����ĐԂŕ`��
plot(ve,xlim=c(0,1),ylim=c(0,1),bty='l',pch=19,col='red',
axes=TRUE, ann=FALSE,asp=1)
}
return(convx)
}
graphics.off()
k=1e3
sim.n(6)
mean(replicate(k,sim.n(6,F,F)))
sim.n(7)
# ����������܂ŒT��(���k��)
seek.concave <- function(n=8,k=1e4){
convex5=TRUE
i=0
while(convex5 & k >0){
convex5=sim.n(n,draw=F)
k=k-1
i=i+1
}
return(i)
}
seek.concave(n=8,k=1e5)
seek.concave(n=9,k=1e6)
������Ė����e���Ɗ��S����B
>>(quote)
���͏��a�̎���ɑ�w�������ǁA�͍̂��������ʊ��������A�c���ȊO�̎�����͓��ꖯ�̂��߂̓���w�Z�Ƃ����C���[�W�ŊJ�ƈ�̃o�J���q�ȊO�͒N�����悤�Ƃ��炵�Ȃ������B
�펯�I�ɍl���āA���疜�Ƃ����@�O�ȋ����āA���������Ǝ҂�������҂�����o�J���̗������̂ƎU�X�l����̂��킩���čD���D��Ŏ�����ɍs���������͈�l�����܂���ł����B
�{�l�ɂ͖ʂƌ������Ă͌���Ȃ�����ǁA�����炢�̔N��̐l�Ԃ́A�����炭�͂W�|�X���͎����������ł��u���̂����Ȃ��Ɣ������Ă�A���̗����o�J���v�ƐS�̒�Ōy�̂��A�}���Ă����B���̖{�l�ɂ͖ʂƌ������Ă͐�ɂ���Ȃ��Ƃ͌���Ȃ����ǂˁB
<<(unquote)
�����Ǝ҂�������҂�����o�J���̗������̂ƎU�X�l����̂��킩���čD���D��Ŏ�����ɍs��
���Ǝ҂̔����F
�y�E�n���z�@�J�ƈ�B�̏W���@8�f�@�y�����z [���f�]�ڋ֎~]©2ch.net
>>
670 ���O�F���̖���������[] ���e���F2017/05/20(�y) 11:15:40.12 ID:46exOAAP
�w��Ő��̈�҂����\���Ă���A�u�n�������̂����ɂ���ׂ��Ă�B�v�Ǝv�����������ɂȂ邪�A
���ꂾ���͊w�����ォ�瑱�����˂Ȃ̂Ŏ~�߂��Ȃ�
<<
���҂̔����F
�y��Áz��҂͊��҂ɃR����������ƁA���S���̂��������b�Ƃ��遚4 [���f�]�ڋ֎~]©2ch.net
>>
810 ���O�F���������P���N[] ���e���F2017/05/21(��) 00:11:22.04 ID:+h+2h2fq0
����㑲�̈�҂��i���҂Ƃ��Ă͌������j
�����̂����ɂ��Ă���̂͂킩���ł��Ȃ���
��ӎ����Ɉ̂����ɂ��ꂽ��
����ኳ�҂Ƃ��Ă͂ނ������낗��
<<
Last but not least,
it is not the kickass bottom medical school but its enrollee that is despicable, which deserves to be called a bona fide moron..
�h��ӃV���c��傪������Ȃ��A�{�l�̓��������B
"���̐���(1)(2)(3)�����ׂĎ��l�ʑ̂����݂��邱�Ƃ��ؖ�����B(1)�ǂ̕ӂ̒��������� (2)�ǂ̖ʂ̖ʐς����� (3)�̐ς�����"
rm(list=ls())
library(numbers)
# while loop version for dec2n
dec2nw <- function(num, N, digit = 4){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
V=function(a,Print=TRUE){
a1=a[1];a2=a[2];a3=a[3];a4=a[4];a5=a[5];a6=a[6]
V2=
a1^2*a5^2*(a2^2+a3^2+a4^2+a6^2-a1^2-a5^2)+
a2^2*a6^2*(a1^2+a3^2+a4^2+a5^2-a2^2-a6^2)+
a3^2*a4^2*(a1^2+a2^2+a5^2+a6^2-a3^2-a4^2)-
a1^2*a2^2*a4^2-a2^2*a3^2*a5^2-a1^2*a3^2*a6^2-a4^2*a5^2*a6^2
if(V2<0) return(0)
else{
v=sqrt(V2)/12
if(Print) cat(v,'\n')
isNatural(v)
}
}
V(c(6,7,8,9,10,11))
S=function(a,Print=TRUE){
a1=a[1];a2=a[2];a3=a[3];a4=a[4];a5=a[5];a6=a[6]
s1=(a1+a2+a4)/2
s2=(a2+a3+a5)/2
s3=(a3+a6+a1)/2
s4=(a4+a5+a6)/2
S1=s1*(s1-a1)*(s1-a2)*(s1-a4)
S2=s2*(s2-a2)*(s2-a3)*(s2-a5)
S3=s3*(s3-a3)*(s3-a6)*(s3-a1)
S4=s4*(s4-a4)*(s4-a5)*(s4-a6)
S2=c(S1,S2,S3,S4)
if(any(S2<0)) return(0)
else{
if(Print) cat(sum(sqrt(S2)),'\n')
all(isNatural(sqrt(S2)))
}
}
S(c(6,7,8,9,10,11))
N=50 # �e�ӂ̍ő咷
Nmin=sum(N^(5:0)) # 1,1,1,1,1,1����J�n
dec2nw(Nmin,N=N)
Nmax=N^6-1
i=Nmin
SV=FALSE # �ʐϑ̐ς����ׂĐ������H
while(!SV & i<Nmax){
i=Nmin
side=dec2nw(i,N)
SV=S(side,F) & V(side,F)
i=i+1
}
dec2nw(i-1,N)
�×{�a���Ζ���E�V���{�Ζ���E���a���Ζ��オ�W���X�����@������ Part.4
http://2chb.net/r/hosp/1550459754/992
992 ���O�F���̖���������[] ���e���F2019/07/20(�y) 19:03:01.20 ID:WRt9tsMe
�����ƊO���̌����߂͊Ō�t���������f��Ȃ���Ƃ��ςȐ��`�������Ă�����_���ė���ł�
�\�ʓI�ɂ͏�����܂��[�A�搶�̂������ł��[�Ƃ������ĂĂ邪���S�͂܂��R�C�c�ɂ�点�Ƃ�����������ĉ��Ɍ��Ă�
���ӂȂ��ĂȂ��A�������o�J���ςɃt�H���[���邹���ŊO���̈�t�����₳�Ȃ�������A�������{�C�Ŋm�ۂ��Ȃ��i�����������j
�L���C�ȃL���L�������a�@�ł������������ƂȂ���͂��̂��Ƃ��킩���ĂȂ��B�u���b�N�a�@�ł͕W�I�ɂ���ėǂ��悤�Ɏg���邾���B
���͉����������Ă���A�����������Ƃ�����Â��Ă���ē����������Ȃ��Ă�߂Ă���
�Ȃ�ɂ����Ȃ����⊳�҂�K���ɂ����炤��t�͐l���o���ł��̂��ƒm���Ă�
�킩���ĂĖ��\�A�o�J�̃t�����Ă�A�C�Â��� >>41
���ݏؖ������Ȃ̂�����
�����ɍS�炸�L�����������邱�Ƃ��ؖ����邾���ł����Ɛ��w�ŋ�������B���ʂȃv���O�����������Ă������B �P�O�O���~�������Ă��鏗�q�吶�Ɠq��������
�ǂɌ������Ėڂ��ނ��Ė���ׂɃ_�[�c����U�{������B
�E�@�@�E
�@�@�E�E�@
�@�E�@�@�E
�̔z�u�̂悤�ɁA�ǂ̂T�_��I��ł��ʌ܊p�`���ł��Ȃ��ꍇ�͏��q�吶�̏����ł��Ȃ��͊|������S�Ď����B
�ʌ܊p�`���ł���T�_��I�ׂ�z�u�Ȃ珗�q�吶����P�O�O���~�����炦��B
�|������������܂łȂ�L���ȓq���Ƃ����邩�H
sim <- function(n=7){
th=runif(n,-pi ,pi)
p2d=function(th,r=1) r*(cos(th)+1i*sin(th))
f <- function(x){
x1=x[1];x2=x[2];x3=x[3]
v1=p2d(th[x1]);v2=p2d(th[x2]);v3=p2d(th[x3])
a=abs(v1-v2);b=abs(v2-v3);c=abs(v3-v1)
s=(a+b+c)/2
S=sqrt(s*(s-a)*(s-b)*(s-c))
2*S/(a+b+c) # S/s
}
sum(combn(n,3,f))
}
replicate(10,sim(7))
�ȒP�ɃV�~�����[�V�����ł���Ǝv���������ƃf�o�b�O�ɋ�J�����B�z���A[0]�������Ȃ�R�ɑΉ����Ă悤�₭�����B
�v���O���~���O�̓��W�J���v�l�̌P���ɂȂ�Ȃ��B
�m�b�x��̃h��ӃV���c�ɂ͖��������ǁB
##
rm(list=ls())
"
�~�ɓ��ڂ����n�p�`(n��4)���A1�̒��_����n-3�{�̑Ίp�����������Ƃɂ���āAn-2�̎O�p�`�ɕ�������B
���̂Ƃ��A�e�O�p�`�̓��ډ~�̔��a�̘a�͕����̎d���ɊW�Ȃ����ł��邱�Ƃ������B
"
sim <- function(n,r=1){
th=c(0,sort(runif(n-1,0,2*pi))) # n�p�`�̕Ίp��(th)��[0,2��]�ŗ������������ă\�[�g���ĕ��ׂ�
p2d=function(x) r*(cos(x)+1i*sin(x)) # �Ɍ`���f����
c2r <- function(v1,v2,v3){ # complex number to radius of inscribed circle
a=abs(v1-v2);b=abs(v2-v3);c=abs(v3-v1) # ���f���Ԃ̋����������ɂ����
s=(a+b+c)/2
S=sqrt(s*(s-a)*(s-b)*(s-c)) # �ʐ�:�w�����̌���
return(S/s) #�@���� r = 2*S/(a+b+c): ���ډ~�̔��a
}
ver=p2d(th) # vertex(���f���\��)
sor=numeric(n) # sum of raius of inscribed circle ���_ver[i]����̑Ίp���ŕ���������
z2n <- function(x,m=n) ifelse(x%%m,x%%m,m) # ���n�̏�]�O�̂Ƃ� n ��Ԃ�
for(i in 1:n){
for(j in 1:(n-2)){
sor[i]=sor[i] + c2r(ver[z2n(i)],ver[z2n(i+j)],ver[z2n(i+j+1)])
}
}
�@return(sor)
}
sim(100)
���吔��������Ƃ����ӂꂱ�݂�Rmpfr���Đ��m����Ȃ��ȁB�T�O�̊K����v�Z�����Ă݂�
R with Rmpfr
> mpfr(factorial(50),1e5)
1 'mpfr' number of precision 100000 bits
30414093201713018969967457666435945132957882063457991132016803840
Haskell:
Prelude> product[1..50]
30414093201713378043612608166064768844377641568960512000000000000
Python:
import math
print(math.factorial(50))
30414093201713378043612608166064768844377641568960512000000000000
Wolfram:
https://www.wolframalpha.com/input/?i=50!
30414093201713378043612608166064768844377641568960512000000000000
�Ǝv���Ă������A
library(Rmpfr)
one = mpfr(1, 5000)
factorial(one*50)
> one = mpfr(1, 5000)
> factorial(one*50)
1 'mpfr' number of precision 5000 bits
[1] 30414093201713378043612608166064768844377641568960512000000000000 library(Rmpfr)
one = mpfr(1, 1000)
a2n <- function(x) as.numeric(paste(as.character(x),collapse=''))
nsplit <- function(x) as.numeric(unlist(strsplit(as.character(x),'')))
n=15*one
( x=sample(n) )
( y=a2n(x) )
( z=na.omit(nsplit(y)) )
sum(z)
�ЊQ���������Ă�����Ƃ���ɏd�ǔ�Ў҂�����B���h������o�����ċ~�}�Z���^�[�Ɋ��҂��������
���h������~�}�Z���^�[�ւ̋�����100km�@�~�}�Ԃ̃K�\������20L�A���҂��悹�Ȃ���Ԃł͔R���10km/L�A���҂��悹�Ă̔R���5km/L�ł���
���҂��~����n��̖ʐς͂�����ɂȂ邩�H
�����̊�nA��������ЂƂ̊�nB�Ɍ������ďo��������Ԃ�GPS�̌̏�Ői�H���������Ă��܂����������ɃK�X���Ŏ~�܂��Ă��܂����B�ʂ̐�ԂŊ�nA���炱�̐�Ԃ~���Ɍ������A�R�����^���Ĉꏏ�Ɋ�nB�ɍs�����ƂɂȂ����B�������A��Ԃɂ�AB�Ԃ����傤�lj����ł��邾�������R���͐ς߂Ȃ��BAB�Ԃ̋�����R�Ƃ��āA�~�o�\�ȗ̈�̖ʐς�R���g���ĕ\���Ȃ����B
�������A��Ԃ̔R��͂�������������̂Ƃ���B
���̃V�~�����[�V�����v���O���~���O���l���Ă�����A�肪����B
���x�����̋��`�̘f��������B
���̘f���̕\�ʓ_P�ł̏d�͂��ő�ɂ��邽�߂ɑ̐ςƖ��x���̏����Řf���̌`��ό`����B
�_P�ł̏d�͂͋��`�̂Ƃ��̍ő剽�{�ɂȂ邩�B
�܂����̂Ƃ��̘f���̌`�͂ǂ��Ȃ邩�B
�����ォ���t�Ƌ��D����B
������w����S�ĉ�̂���B
�{���Ȃ瓞���t�ɂȂꂸ�A
�J�l�ň�҂ɂȂ����j�Z��҂𔗊Q���ԊO��ɂ��ċ��e���傤�I
�z��̍s���͊��ҎE���ƍ�����ւ̋t���ʁA�����点�ł���B
������̊��ҎE���������ȁI
rm(list=ls())
graphics.off()
curve( sqrt(1-x^2), xlim=c(-1,1), ylim=c(-1,1), asp=1)
curve(-sqrt(1-x^2), xlim=c(-1,1), ylim=c(-1,1), add=T)
cir <- function(ce,r,...){
a=ce[1];b=ce[2] # (x-a)^2+(y-b)^2=r^2 ,y = b �} ��(r^2-(x-a)^2)
curve(b+sqrt(r^2-(x-a)^2),xlim=c(a-r,a+r),ylim=c(b-r,b+r),asp=1,bty='l',...)
curve(b-sqrt(r^2-(x-a)^2),add=TRUE)
}
circle <- function(z,r,...){
if(is.complex(z)){ a=Re(z) ; b=Im(z)
}else{ a=z[1] ; b=z[2] }
x=seq(a-r,a+r,length=100)
y=b+sqrt(r^2-(x-a)^2)
plot(x,y,ylim=c(b-r,b+r),type='l',bty='l',...)
lines(x,2*b-y,...)
}
circle(c(1,3),5,lwd=2,col='maroon')
plot.circle <- function(x, y, r, ...){
theta <- seq(-pi, pi, length=100)
plot(x + r*cos(theta), y + r*sin(theta), type="l", asp=1, bty='l', ...)
}
plot.circle(1,2,3)
>>52
�V�~�����[�V�����̏����Ɂ@�܂��A���_����l���z�z�u���Ȃ�����Ȃ��B

���Ⴞ�߂�

���� �����ȑO�Ɉ��{�̋c�����i�ɋ^�╄�����Ă����ł����c
�܂����������ł̌���ɂ��L���Ҕ�����
���E�I���@�ᔽ�Ȃ�Ȃ���ł����H
# �P�ʉ~����N�̓_����l���z�Ŕ���������
N=1e3
zt=0i
z=NULL
while(length(z) < N){
zt=sum(runif(2,-1,1)*c(1,1i))
if(abs(zt)<=1) z=append(z,zt)
}
plot(z,asp=1,bty='l',ann=F) ; points(p,pch='+',cex=2)
rm(list=ls())
library(gtools)
a=permutations(2,15,rep=T)
no21 <- function(x) { # 1�̘A���͖����Ƃ�TRUE��Ԃ� No Two one
( y=rle(x) ) # run length endcoding �ŘA���p�x���X�g
( z=matrix(unlist(y),nrow=2,byrow=T) ) # �s��ɂ���
( i1=which(z[2,]==1) ) # 1�̕p�x��z��
all(z[1,i1]<2) # ���ׂĂQ�����ł����TRUE
}
no21i=which(apply(a,1,no21)) # no21i : 1���A�����Ȃ�a��index�i�s�ԍ�)
b=a[no21i,] # b:����ɊY������s��
step15 <- function(x){ # �ݐϘa���r����15�ɂȂ��TRUE��Ԃ� step15
15 %in% cumsum(x)
}
s15i=which(apply(b,1,step15)) # s15i�ݐϘa���r����15�ɂȂ�b��index�i�s�ԍ�)
c=b[s15i,] # b:����ɊY������s��
stp15 <- function(x){ # �P�T�i�ɂȂ�܂ł�step��Ԃ�
i=which(cumsum(x)==15)
if(length(i)!=0) return(x[1:i])
else return(NULL)
}
d=apply(c,1,stp15)
unique(d)
1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A1����2�i���邱�Ƃ͘A�����Ȃ����̂Ƃ���B15�i�̊K�i�����鏸����͉��ʂ肠�邩�����߂�B
>>59
13�i�̕���������������邩�ȁB >>60
999�i�̂Ƃ��@72428926648244374994035719791113496129988312942838688570843879389313216865724883592391343074367517004225503378684709437440�@�ʂ�ɂȂ������A
���l�v�Z���x�̐���듚���������B
�h��ӃV���c��ł������炢�������邾�낤����A���ɏ����Đ����Ă���B
13�i�̏ꍇ���Ƃ���Ȋ����B
[[1]]
[1] 1 2 1 2 1 2 1 2 1
[[2]]
[1] 1 2 1 2 1 2 2 2
[[3]]
[1] 1 2 1 2 2 1 2 2
....
[[27]]
[1] 2 2 2 2 2 1 2
[[28]]
[1] 2 2 2 2 2 2 1 >>61
�s�蒷���̈�����Haskell�@����
72428926648244409475025064434360344869036057631812487293633154973026123860267808630768185105127650714516006185052479679199
�ɂȂ����B Python�ł�
N=1000
f = [0]*N
f[0]=1
f[1]=1
f[2]=2
for n in range(0,N-3):
f[n+3]=f[n+1]+f[n]
print (f[999-1])
72428926648244409475025064434360344869036057631812487293633154973026123860267808630768185105127650714516006185052479679199
��Haskell�̌��ʂƈ�v
���R����z�M����Ă����̂����A�ŋ߂̍������Ĕn������҂ɂ����肾�炯���ȁB
��112���t������聟
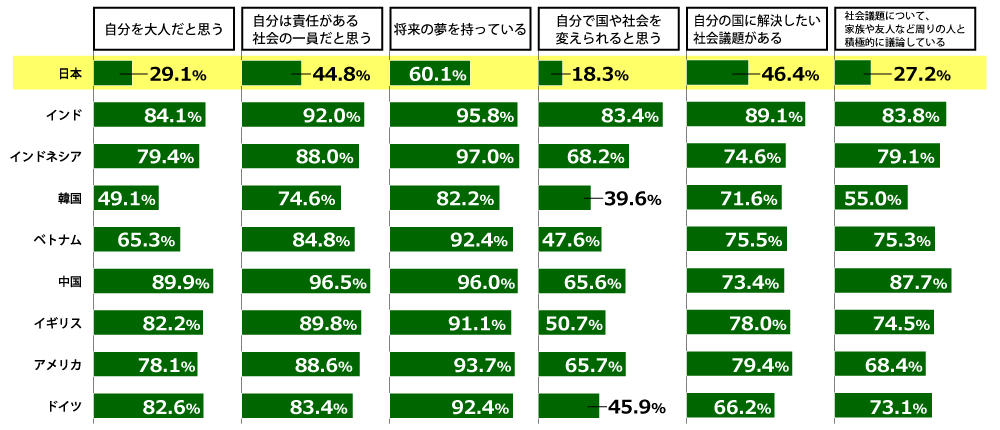
���₯�̗U���ƂȂ�ɂ����̂͂ǂꂩ�B
����112-��112���t���Ǝ�����������i��w�]�_�Ёj���o��@�w��������80.2��
A �ߐH
B �^��
C �얞
D �����b�H
E �O���p��
�������������o���āA�������w�̃V���c��w����r�����ׂ����Ǝv����Ȃ��B
1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A1����2�i���邱�Ƃ͘A�����Ȃ����̂Ƃ���B15�i�̊K�i�����鏸����͉��ʂ肠�邩�����߂�B
�����������^�Ȗ��ŏꍇ�������Čn���I�ɃJ�E���g�ł��邩��₤���͑��l�̌��ʂƍ��v����Ǝ����̌v�Z�Ɋm�M�����Ă�B
1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A2���ő����ď��邱�Ƃ�3��ȏ�͘A�����Ȃ����̂Ƃ���B�i2����2���ŏ���͉̂j
15�i�̊K�i�����鏸����͉��ʂ肠�邩�����߂�B
���ɕ`���ꂽ�A������x�傫�ȉ~�̉~����ɐl��A�����āA�~�̒��S�ɐl��B������B
���āA���̂悤�ȃQ�[��������B
��A��B��߂܂���̂��ړI�B�������A�~���サ�������Ȃ��B
��B��A�ɕ߂܂炸�ɉ~���ɓ�������̂��ړI�B���̍ہA�~���Ɍ������Ă܂����������Ă��������A�r���Ō�����ς��Ă������B�܂��A���Ӗ��Ȏ��ԉ҂��͂��Ȃ�(�X�^�[�g�n�_�ɉ����Ԃ��������ɂ���etc.)�B
�y���zA��B��߂܂��邽�߂ɂ́AA�̑��x��B�̑��x�̉��{�ȏ�łȂ���Ȃ�Ȃ����B�������AA��B�̑��x�͈��Ƃ��A���݂��őP��s�������̂Ƃ���B
�y���zB��A�̂���ꏊ�Ƃ͐����̕����Ɍ������Ă܂������s���ƁAB�̈ړ������͔��ar�AA�̈ړ������͔��~����r�Ȃ̂ŁAA��B�̃Δ{�̑����ōs���ƁAB���~���ɓ��������u�Ԃ�B��߂܂�����A�̏����A�Δ{�����Ȃ��B�̏����ƂȂ邪�A�ʂ�����B�̂��̍s���͍őP�Ȃ̂��H
circle <- function(z,r,...){
if(is.complex(z)){ a=Re(z) ; b=Im(z)
}else{ a=z[1] ; b=z[2] }
x=seq(a-r,a+r,length=100)
y=b+sqrt(r^2-(x-a)^2)
plot(x,y,ylim=c(b-r,b+r),asp=1,type='l',bty='l',...)
lines(x,2*b-y,...)}
# draw segment of complex a to complex b
seg <- function(a,b,...){
segments(Re(a),Im(a),Re(b),Im(b),col=2,...)}
# draw text y at complex x
pt <- function(x,y=NULL,...){
text(Re(x),Im(x), ifelse(is.null(y),'+',y), ...)}
p2d <- function(th,r=1) r*(cos(th)+1i*sin(th))
sim <- function(v=pi){
circle(0i,1) ; points(0+0i,pch='B',col=2) ; points(-1+0i,pch='A')
for(n in 1:20){
t=0.05
pt(p2d(pi+v*t*n),n)
pt(p2d(v*t*n,t*n),n,col=2)
}
}
sim(pi)
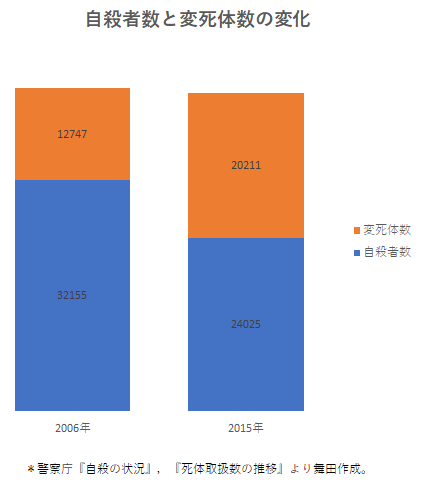
2018�N2��5�����j��
���E�҂ƕώ���
�ŋ߂ł́C�⏑��ڌ��،��Ƃ�������̓I�ȏ؋����Ȃ�����C���E�Ƃ͔F�߂��C�ώ��̂Ƃ��ď�������悤�ɂȂ����Ɓi��L�L���j�B
���v��̎��E�Ґ��Ƃ����̂́C����̂��������œ������̂ł��B���v�ɂ͕\��Ȃ��u�Ð��v�Ɏv�������点�Ȃ��Ƃ����܂���B
http://tmaita77.blogspot.com/2018/02/blog-post_5.html
N=100
A = [0]*N
A[0] = 1
A[1] = 1
A[2] = 2
for n in range(3,N):
A[n] = (A[n-1] + A[n-3])
print (A[N-1]+A[N-3])
>>66
���������ӂ��ɓ������

�g�����v�����čݓ��ČR�������グ������A���{�̊j������e�F���������Ă����킯�ŁA
���{����������ō��̃`�����X�������B
���������ꂷ��������������̐헪���Ȃ��A�����J�̌��ł��葱�����̂����{���������B
���ꂾ���łȂ����{���l�I���x�O���[�o���X�g�ŕێ�I����͉����炸�ɔ��������͖҃X�s�[�h�Ŏ��X�ɐ��������Ă��錻��������A
���{�̖{�����Ȃɂ��Ȃ�Ĕn���ł��킩���肾�낤���B
���炩�Ɉ��{��DS�̃X�p�C�Ȃ킯�����A100�������ĉ��ɂ����ł͂Ȃ��d���Ȃ�����������Ă���Ɖ��肵�Ă�
���{�����̍ő�̃`�����X���牽�����������ɃA�����J�̌�����葱���A
�ێ�I����͉����炸�ɔ��������͖҃X�s�[�h�Ŏ��X�ɐ��������Ă���킯�ŁA
�ێ�ɂƂ��ĉ��̃����b�g���Ȃ������ŁA�������|�t�����{�̔j����~�߂�����ȊO�̑I�����͂Ȃ��B
�����͈��{�����ɉ��S�������Ă��锄���z�Ƃ��ĉ�X�ێ�͐�ɋ����킯�ɂ͂�����B
>>415
�����}���@��������(�{������)
�E��12��
���@�������ɕۏႷ�鎩�R�y�ь����́A�����̕s�f�̓w�͂ɂ��A�ێ�����Ȃ���Ȃ�Ȃ��B
�����́A����𗔗p���Ă͂Ȃ炸�A���R�y�ь����ɂ͐ӔC�y�ы`�����������Ƃ����o���A��Ɍ��v�y�ь��̒����ɔ����Ă͂Ȃ�Ȃ��B
�E��13��
�����A���R�y�эK���Nj��ɑ��鍑���̌����ɂ��ẮA���v�y�ь��̒����ɔ����Ȃ�����A���@���̑��̍����̏�ŁA�ő���ɑ��d����Ȃ���Ȃ�Ȃ��B
�E��14��-3
(���s)�h�_�A�M�͂��̑��h�T�̎��^�́A�����Ȃ���T������Ȃ��B
��
(����)
�h�_�A�M�͂��̑��h�T�̎��^�́A���ɂ����L���A���͏����������҂̈��Ɍ���A���̌��͂�L����B
�E��18��
(���s)���l���A�����Ȃ�z��I�S�����Ȃ��B
��
(����)�Љ�I���͌o�ϓI�W�ɂ����Đg�̂��S������Ȃ��B
�E��29��
���Y���̓��e�́A���v�y�ь��ɂ����̒����ɓK������悤�ɁA�@���Œ�߂�B
�E��97��
(���s)���̌��@�����{�����ɕۏႷ���{�I�l���́A�l�ނ̑��N�ɂ킽�鎩�R�l���̓w�͂̐��ʂł��āA
�����̌����́A�ߋ������̎��B�Ɋ��ցA���y�я����̍����ɑ��A�N�����Ƃ̂ł��Ȃ��i�v�̌��Ƃ��ĐM�����ꂽ���̂ł���B
��
(����)�S���폜 A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A���̂悤�ɏ،����Ă���B���̂Ƃ��A�R���͒N���A�S�ē�����B
A�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�����҂�����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�����҂�����v
D�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�����҂�����v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�R��������v
H�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�R��������v
rm(list=ls())
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
ah=sapply(0:255,function(x) dec2nw(x,2,8))
AH=t(ah)
AH=rbind(c(8,0),t(apply(AH[c(-1,-256),],1,table)),c(0,8))
AH
rm(list=ls())
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
ah=sapply(0:(2^n-1),function(x) dec2nw(x,2,n))
AH=t(ah)
tf=rbind(c(n,0),t(apply(AH[c(-1,-(2^n-1),],1,table)),c(0,n))
tf
"
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A���̂悤�ɏ،����Ă���B���̂Ƃ��A�R���͒N���A�S�ē�����B
A�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�����҂�����v tf[,2]
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�����҂�����v
D�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�����҂�����v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�R��������v
H�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�R��������v
"
rm(list=ls())
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
ah=sapply(0:(2^n-1),function(x) dec2nw(x,2,n))
AH=t(ah)
AH
tf=rbind(c(n,0),t(apply(AH[c(-1,-(2^n)),],1,table)),c(0,n))
tf
A�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�����҂�����v tf[,2]>=1
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v tf[,2]>=2
C�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�����҂�����v tf[,2]>=3
D�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�����҂�����v tf[,2]>=4
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v tf[,1]>=1
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v tf[,1]>=2
G�u8�l�̒��ɁA���Ȃ��Ƃ�3�l�R��������v tf[,1]>=3
H�u8�l�̒��ɁA���Ȃ��Ƃ�4�l�R��������v tf[,1]>=4
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
te=sapply(0:(2^n-1),function(x) dec2nw(x,2,n)) # testimony
TE=t(te)
f <- function(x){
H=sum(x)
L=n-H
all(c(H>0,H>1,H>2,H>3,L>0,L>1,L>2,L>3)==x)
}
apply(TE,1,f)
�ʋΒ��ɉ������Ă��܂����B
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
te=sapply(0:(2^n-1),function(x) dec2nw(x,2,n)) # testimony
TE=t(te)
f <- function(x){
H=sum(x)
L=n-H
all(c(H>0,H>1,H>2,H>3,L>0,L>1,L>2,L>3)==x)
}
TE[apply(TE,1,f),]
> TE[apply(TE,1,f),]
[1] 1 1 1 1 1 1 0 0
�����������ɂ����
A�u8�l�̒��ɁA1�l�����҂�����v
B�u8�l�̒��ɁA2�l�����҂�����v
C�u8�l�̒��ɁA3�l�����҂�����v
D�u8�l�̒��ɁA4�l�����҂�����v
E�u8�l�̒��ɁA1�l�R��������v
F�u8�l�̒��ɁA2�l�R��������v
G�u8�l�̒��ɁA3�l�R��������v
H�u8�l�̒��ɁA4�l�R��������v
�ʔ����B
�������̕����ʔ����B
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A���̂悤�ɏ،����Ă���B���̂Ƃ��A�R���͒N���A�S�Ă̑g��������B
A�u8�l�̒��ɁA1�l�R��������v
B�u8�l�̒��ɁA2�l�R��������v
C�u8�l�̒��ɁA3�l�R��������v
D�u8�l�̒��ɁA4�l�R��������v
E�u8�l�̒��ɁA5�l�R��������v
F�u8�l�̒��ɁA6�l�R��������v
G�u8�l�̒��ɁA7�l�R��������v
H�u8�l�̒��ɁA8�l�R��������v
���̗ǂ��͂����������ł͖����Ǝv���̂ł���
# �R���͕K���R�̏،�������ݒ�ɕύX
dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
te=sapply(0:(2^n-1),function(x) dec2nw(x,2,n)) # testimony
TE=t(te)
f <- function(x){
H=sum(x)
L=n-H
all(c(
ifelse(x[1],H>=1,H<1),
ifelse(x[2],H>=2,H<2),
ifelse(x[3],H>=3,H<3),
ifelse(x[4],H>=4,H<4),
ifelse(x[5],L>=1,L<1),
ifelse(x[6],L>=2,L<2),
ifelse(x[7],L>=3,L<3),
ifelse(x[8],L>=4,L<4)
)==x)
}
TE[apply(TE,1,f),]
�R����l���łȂ��ē��肷��،����܂߂Ă݂�B
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A���̂悤�ɏ،����Ă���B�،��ł��R���͕K���R�����B
�R���͒N���A�S�Ă̑g��������B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC�͉R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v

dec2nw <- function(num, N=2, digit){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
n=8
te=sapply(0:(2^n-1),function(x) dec2nw(x,2,n)) # testimony
TE=t(te)
f <- function(x){
H=sum(x) ; cat(H,'\n')
L=n-H
all(c(
(x[1]==1 & H>=1) | x[1]==0 & H<1,
(x[2]==1 & H>=2) | x[2]==0 & H<2,
(x[3]==1 & H>=3) | x[3]==0 & H<3,
(x[4]==1 & H>=4) | x[4]==0 & H<4,
(x[5]==1 & L>=1) | x[5]==0 & L<1,
(x[6]==1 & L>=2) | x[6]==0 & L<2,
(x[7]==1 & L>=3) | x[7]==0 & L<3,
(x[8]==1 & L>=4) | x[8]==0 & L<4
))
}
TE[apply(TE,1,f),]
>>85
�f�o�b�O�I���i�̂���j
##
"A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
���̂悤�ɏ،����Ă���B�،��ł��R���͕K���R�����B
�R���͒N�����ׂē�����B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC�͉R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v
"
TE=gtools::permutations(2,8,v=0:1,rep=T)
g <- function(x){
H=sum(x) # H:�����҂̐�
L=n-H # H:�R���̐�
all(c( # �S�Đ��������TRUE��Ԃ�
(x[1]==1 & H==3) | (x[1]==0 & H!=3 ), # A�������҂ŏ،��������� | A���R���ŏ،����R
(x[2]==1 & H>=2) | (x[2]==0 & H <2 ), # B�������҂ŏ،��������� | B���R���ŏ،����R
(x[3]==1 & x[2]==0) | (x[3]==0 & x[2]==1),
(x[4]==1 & x[3]==0) | (x[4]==0 & x[3]==1),
(x[5]==1 & L>=1) | (x[5]==0 & L<1 ),
(x[6]==1 & L>=2) | (x[6]==0 & L<2 ),
(x[7]==1 & x[5]==0) | (x[7]==0 & x[5]==1),
(x[8]==1 & x[1]==0 & x[6]==0) | (x[8]==0 & (x[1]==1 | x[6]==1))
))
}
TE[apply(TE,1,g),] �ǂ����ɁA��肪�Ȃ����ƒT���Ă�����A���w�����̖�肪������
"�`�A�a�A�b�A�c�A�d�̂T�l�̂����Q�l�͏�ɖ{���̂��Ƃ����������҂ł��B\n���Ƃ̂R�l�͉R���ł����A���̔������e�͖{���̂Ƃ�������܂��B\n�ނ�ɒN���R�����q�˂��Ƃ��뎟�̂悤�ɓ����܂����B\n\n�`�@�u�a�Ƃd�͉R���ł͂Ȃ��v\n�a�@�u�b�͉R�����v\n�b�@�u�c�͉R�����v\n�c�@�u�d�͉R�����v\n�d�@�u�a�Ƃb�͉R�����v\n���āA�����҂͒N�ƒN�ł��傤���H"
> TE=gtools::permutations(2,5,0:1,rep=T)
> f <- function(x){
+ if(sum(x)!=2){ return(FALSE)
+ }else{
+ all(c(
+ (x[1]==1&x[2]==1&x[5]==1) | x[1]==0,
+ (x[2]==1&x[3]==0) | x[2]==0,
+ (x[3]==1&x[4]==0) | x[3]==0,
+ (x[4]==1&x[5]==0) | x[4]==0,
+ (x[5]==1&x[2]==0&x[3]==0) | x[5]==0))
+ }
+ }
> LETTERS[1:5][TE[apply(TE,1,f),]==1]
[1] "B" "D"
���܂����삵�Ă���I
�`�A�a�A�b�A�c�A�d�̂T�l�̂����Q�l�͏�ɖ{���̂��Ƃ����������҂ł��B���Ƃ̂R�l�͉R���ł����A���̔������e�͖{���̂Ƃ�������܂��B
�ނ�ɒN���R�����q�˂��Ƃ��뎟�̂悤�ɓ����܂����B
�`�@�u�a�Ƃd�͉R���ł͂Ȃ��v
�a�@�u�b�͉R�����v
�b�@�u�c�͉R�����v
�c�@�u�d�͉R�����v
�d�@�u�a�Ƃb�͉R�����v
���āA�����҂͒N�ƒN�ł��傤���H
>>82
�����A�h��ӁB
����ɓ����Ă݁I���w�������̖�肾���ǁB
����h��ӃV���c���̐V������101�l�Ƃ���B
101�l�͊w�͍l���œ��w�������K�w���Ƌ��œ����������w���̂ǂ��炩�ł���B
���K�w���͏�ɖ{���̂��Ƃ����A�����w���͋���������Ȃ��B
�S�Ă̊w���͒N�������w������m���Ă���B
�w���S���ɗ����w���͉��l���邩��q�˂��Ƃ���
�w��A1�u1�l�ȏ�̗����w��������v
�w��A2�u2�l�ȏ�̗����w��������v
�w��A3�u3�l�ȏ�̗����w��������v
...
�w��A99�u99�l�ȏ�̗����w��������v
�w��A100�u100�l�ȏ�̗����w��������v
�w��A101�u�S���������w���ł���v
�Ƃ̏،����B
�ȏ�̏�炱�̃h��ӃV���c���̗����w���͒N�����q�ׂ�B >>87
�X�ɁA�R�������ǂ����킩��Ȃ��t�@�W�[�Ȑl�����Q�������Ė��ɂ��Ă݂��B
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����m���ɐ����҂ƒf��ł�����̂�S�ċ�����B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC�͉R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v
TE=gtools::permutations(2,n,v=0:1,rep=T)
colnames(TE)=LETTERS[1:n]
k <- function(x){
H=sum(x) # H:�����҂̐�
L=n-H # H:�R���̐�
all(c( # �S�Đ��������TRUE��Ԃ�
(x[1]==1 & H==3) | (x[1]==0 & H!=3 ), # A�������҂ŏ،��������� | A���R���ŏ،����R
(x[2]==1 & H>=2) | (x[2]==0 & H <2 ), # B�������҂ŏ،��������� | B���R���ŏ،����R
(x[3]==1 & x[2]==0) | (x[3]==0 & x[2]==1),
(x[4]==1 & x[3]==0) | (x[4]==0 & x[3]==1),
(x[5]==1 & L>=1) | (x[5]==0 & L<1 ),
(x[6]==1 & L>=2) | (x[6]==0 ),
(x[7]==1 & x[5]==0) | (x[7]==0 ),
(x[8]==1 & x[1]==0 & x[6]==0) | (x[8]==0 ) ) )
}
TE[apply(TE,1,k),] ���r�炵�H���
��ӎ�����̎��ԃo�������Ǝ��l���ł邩���
>>92
�ǂ̖��ɂ��̏o���Ȃ��A�z���I >>91
���w�ɏ�������A�v���O�����ʼn������Ɖ��̂Ƃ͈Ⴄ���o�Ă����̂ō��f���Ă�����
�_�ʼn��Ă��ꂽ�l�����āA���̉ƈ�v���Ă����̂ʼn��̃v���O�����̕����������Ɗm�M�ł��Ăق��Ƃ����B
���̃X���ɂ̓h��ӓ��]�����A���Ȃ��悤���ȁB >>93
�Y�{�V�ŕK������
���˃L�`�K�C >>95
�ǂꂩ�����Ă݁I
�h��ӓ��]�N�� ���`���A�h��ӁB
����ɓ����Ă݁I���w�������̖�肾���ǁB
����h��ӃV���c���̐V������101�l�Ƃ���B
101�l�͊w�͍l���œ��w�������K�w���Ƌ��œ����������w���̂ǂ��炩�ł���B
���K�w���͏�ɖ{���̂��Ƃ����A�����w���͋���������Ȃ��B
�S�Ă̊w���͒N�������w������m���Ă���B
�w���S���ɗ����w���͉��l���邩��q�˂��Ƃ���
�w��A1�u1�l�ȏ�̗����w��������v
�w��A2�u2�l�ȏ�̗����w��������v
�w��A3�u3�l�ȏ�̗����w��������v
...
�w��A99�u99�l�ȏ�̗����w��������v
�w��A100�u100�l�ȏ�̗����w��������v
�w��A101�u�S���������w���ł���v
�Ƃ̏،����B
�ȏ�̏�炱�̃h��ӃV���c���̗����w���͒N�����q�ׂ�B
�������ł�>97�̗����w�����N���������Ȃ��Ȃ痠���w�����x���̓��]���ˁB
�t�F���}�[�̍ŏI�藝�̔��Ⴊ������
������݂�����̂́A����͂���Ő����ȁB

�O������Ă��Ă��P�ꂵ����b�ł��Ȃ��m�b�x����Ă����ȁB
�����A�h��ӁB
����ɓ����Ă݁I���w�������̖�肾���ǁB
����h��ӃV���c���̐V������101�l�Ƃ���B
101�l�͊w�͍l���œ��w�������K�w���Ƌ��œ����������w���̂ǂ��炩�ł���B
���K�w���͏�ɖ{���̂��Ƃ����A�����w���͋���������Ȃ��B
�S�Ă̊w���͒N�������w������m���Ă���B
�w���S���ɗ����w���͉��l���邩��q�˂��Ƃ���
�w��A1�u1�l�ȏ�̗����w��������v
�w��A2�u2�l�ȏ�̗����w��������v
�w��A3�u3�l�ȏ�̗����w��������v
...
�w��A99�u99�l�ȏ�̗����w��������v
�w��A100�u100�l�ȏ�̗����w��������v
�w��A101�u�S���������w���ł���v
�Ƃ̏،����B
�ȏ�̏�炱�̃h��ӃV���c���̗����w���͒N�����q�ׂ�B
>>99
�����T���X�N���v�g�������Ă݂��B
options(scipen = 10)
n=1000
cmb=gtools::combinations(n,2)
cmb=cmb[cmb[,1]<cmb[,2],]
dsplit <- function(x){ # digit split for natural number
y=unlist(strsplit(as.character(x),''))
if('.' %in% y) return(NULL)
else as.numeric(unlist(y))
}
a2d <- function(x) as.numeric(paste(as.character(x),collapse=''))
f <- function(xy){
x=xy[1] ; y=xy[2]
x3=x^3 ; y3=y^3
a=dsplit(x3) ; b=dsplit(y3)
y3 ; b
dl=length(b)-length(a)
a0=append(rep(0,dl),a)
c=a0+b
c2=a2d(c)
c3=c2^(1/3)
d=round(c3,10)
if(numbers::isNatural(d)) return(d)
else return(0)
}
idx=which(apply(cmb,1,f)>0)
cmb[idx,] >>106
�R���܂ł̐����ł́A�摜�ɂ���P�g�������ȁB
> cmb[idx,]
[1] 70 212 1cm���݂̐�������ׂ̗荇����3�_�Ɂ�������(3�́��͋�ʂ��Ȃ�)�B
1�b���ƂɁ�1�����́�1���щz���B
���̏ꍇ�A����Ƃ́��̈ʒu�́A��щz���ꂽ������̋��������Ƃ̈ʒu����Ɠ����ɂȂ�悤�ɂ���B
����Ƃ̈ʒu�ɂ��łɑ��́�������Ƃ��͔�ׂȂ��B
2021�b��ɁA�������S�Ă��J�n�ʒu�ɖ߂邱�Ƃ͂ł��邩�H
��A
�@�@�@������
����������������������
��
�@�@�@���@����
����������������������
��
�@���@���@�@��
����������������������
��
�@���@�@�@�@���@�@��
����������������������
��
�F
��
�@�@�@������
AB <- function(abc){
a=abc[1];b=abc[2];c=abc[3]
y=b+b-a
if(y>=c) return(abc)
else return(c(b,y,c))
}
BC <- function(abc){
a=abc[1];b=abc[2];c=abc[3]
c(a,c,2*c-b)
}
BA <- function(abc){
a=abc[1];b=abc[2];c=abc[3]
c(a-(b-a),a,c)
}
CB <- function(abc){
a=abc[1];b=abc[2];c=abc[3]
y=b-(c-b)
if(y<=a) return(abc)
else return(c(a,y,b))
}
J=c(AB,BC,BA,CB)
jump <- function(x){
j=J[[sample(4,1)]](x)
while(all(j==x)){
j=J[[sample(4,1)]](x)
}
return(j)
}
lim=1e5
sim <- function(x=c(1,2,3)){
cat(0, ': ',x,'\n')
j=jump(x)
i=1
cat(i, ': ',j,'\n')
while(any(j!=x) & -lim<min(j) & max(j)<lim){
j=jump(j)
i=i+1
cat(i, ': ',j,'\n')
}
}
sim()
���̃W�����v�ŕ��A����ˁB
> sim()
0 : 1 2 3
1 : 1 3 4
2 : 1 4 5
3 : -2 1 5
4 : 1 4 5
5 : -2 1 5
6 : 1 4 5
7 : 1 5 6
8 : 1 4 5
9 : 1 3 4
10 : -1 1 4
11 : 1 3 4
12 : 1 2 3
�p��ɕύX���܂��B
> Sys.setenv(LANGUAGE="en")
> fisher.test(c(1,2,3,4))
Error in fisher.test(c(1, 2, 3, 4)) :
if 'x' is not a matrix, 'y' must be given
> Sys.getenv("LANGUAGE")
[1] "en"
>
Sys.setenv��LANGUAGE��en�ɐݒ肷��ƁA���b�Z�[�W���p��ɂȂ�܂��B
�G���[���b�Z�[�W�̕\�����p��ɂȂ��Ă��܂��B
��قǂ͋���Sys.getenv("LANGUAGE")�̌��ʂ�"en"���Ԃ��Ă��܂��B
���{��ɖ߂��܂��B
> Sys.setenv(LANGUAGE="ja")
> fisher.test(c(1,2,3,4))
�ȉ��ɃG���[ fisher.test(c(1, 2, 3, 4)) :
'x' ���s��łȂ���A'y' ��^���Ȃ���Ȃ�܂���
> Sys.getenv("LANGUAGE")
[1] "ja"
��������̕������Ƃ��Ă͔������ȁB
"A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����m���ɐ����҂ƒf��ł�����̂�S�ċ�����B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v
"
n=8
TE=gtools::permutations(2,n,v=0:1,rep=T)
colnames(TE)=LETTERS[1:n]
k <- function(x){
H=sum(x) # H:�����҂̐�
L=n-H # H:�R���̐�
all(c( # �S�Đ��������TRUE��Ԃ�
(x[1]==1 & H==3) | (x[1]==0 & H!=3 ) , # A�������҂ŏ،��������� | A���R���ŏ،����R
(x[2]==1 & H>=2) | (x[2]==0 & H <2 ) , # B�������҂ŏ،��������� | B���R���ŏ،����R
(x[3]==1 & x[2]==0) | (x[3]==0 & x[2]==1) ,
(x[4]==1 & x[3]==0 & x[6]==0) | (x[4]==0 & !(x[3]==0 & x[6]==0)) ,
(x[5]==1 & L>=1) | (x[5]==0 & L<1 ) ,
(x[6]==1 & L>=2) | (x[6]==0 ),
(x[7]==1 & x[5]==0) | (x[7]==0 ),
(x[8]==1 & x[1]==0 & x[6]==0) | (x[8]==0 ) ) )
}
TE[apply(TE,1,k),]
>>108
> ans
[,1] [,2] [,3]
[1,] 1 3 4
[2,] -1 1 4
[3,] -1 4 7
[4,] -1 1 4
[5,] -3 -1 4
[6,] -3 4 9
[7,] -10 -3 9
[8,] -3 4 9
[9,] -3 9 14
[10,] -3 4 9
[11,] -3 -1 4
[12,] -5 -3 4
[13,] -5 4 11
[14,] -5 11 18
[15,] -5 18 25
[16,] -28 -5 25
[17,] -5 18 25
[18,] -5 11 18
[19,] -5 4 11
[20,] -5 11 18
[21,] -5 18 25
[22,] -5 11 18
[23,] -5 4 11
[24,] -14 -5 11
[25,] -14 11 27
[26,] -14 -5 11
[27,] -5 4 11 [28,] -5 -3 4
[29,] -3 -1 4
[30,] -3 4 9
[31,] -3 9 14
[32,] -3 14 19
[33,] -20 -3 19
[34,] -3 14 19
[35,] -3 9 14
[36,] -3 4 9
[37,] -3 -1 4
[38,] -5 -3 4
[39,] -5 4 11
[40,] -5 -3 4
[41,] -3 -1 4
[42,] -3 4 9
[43,] -3 -1 4
[44,] -5 -3 4
[45,] -7 -5 4
[46,] -9 -7 4
[47,] -7 -5 4
[48,] -7 4 13
[49,] -18 -7 13
[50,] -18 13 33
[51,] -18 -7 13
[52,] -7 4 13
[53,] -18 -7 13
[54,] -7 4 13
[55,] -7 13 22
[56,] -27 -7 22
[57,] -7 13 22
[58,] -7 22 31
[59,] -7 31 40
[60,] -7 22 31
[61,] -7 13 22
[62,] -7 22 31
[63,] -36 -7 31
[64,] -7 22 31
[65,] -36 -7 31
[66,] -7 22 31
[67,] -36 -7 31
[68,] -7 22 31
[69,] -7 13 22
[70,] -27 -7 22
[71,] -7 13 22
[72,] -7 4 13
[73,] -18 -7 13
[74,] -18 13 33
[75,] -18 33 53
[76,] -18 53 73
[77,] -89 -18 73
[78,] -89 73 164
[79,] -251 -89 164
[80,] -251 164 417
[81,] -251 -89 164
[82,] -89 73 164
[83,] -89 -18 73
[84,] -89 73 164
[85,] -89 164 255
[86,] -89 73 164
[87,] -89 -18 73
[88,] -160 -89 73
[89,] -160 73 235
[90,] -160 -89 73
[91,] -89 -18 73
[92,] -18 53 73
[93,] -18 33 53
[94,] -18 53 73
[95,] -18 33 53
[96,] -18 53 73
[97,] -89 -18 73
[98,] -18 53 73
[99,] -18 73 93
[100,] -18 53 73
[101,] -18 33 53
[102,] -18 13 33
[103,] -18 -7 13
[104,] -7 4 13
[105,] -7 -5 4
[106,] -5 -3 4
[107,] -3 -1 4
[108,] -1 1 4
[109,] 1 3 4
[110,] 1 2 3
�悤�₭�A���A�I
�V���c��͂₭���Ɠ���
�唼���`����
�ŋ��ҕt�Ŏ����E��
�_���I�v�l�����������
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̒�����m���ɐ����҂ƌ�����̂͒N���H
A�u8�l�̒��ɁA�����҂�3�l����v
B�uH�͉R���ł���v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F�������҂ł���v
�ޑ�
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����N���m���ɐ����҂ƒf��ł��邩�H
A�u�R���̕��������҂�葽���v
B�uH�͉R���ł���v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F�������҂ł���v
2013�N�̔���

��

require(stats); require(graphics)
summary(anscombe)
##-- now some "magic" to do the 4 regressions in a loop:
ff <- y ~ x
mods <- setNames(as.list(1:4), paste0("lm", 1:4))
for(i in 1:4) {
ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
## or ff[[2]] <- as.name(paste0("y", i))
## ff[[3]] <- as.name(paste0("x", i))
mods[[i]] <- lmi <- lm(ff, data = anscombe)
print(anova(lmi))
}
## See how close they are (numerically!)
sapply(mods, coef)
lapply(mods, function(fm) coef(summary(fm)))
## Now, do what you should have done in the first place: PLOTS
op <- par(mfrow = c(2, 2), mar = 0.1+c(4,4,1,1), oma = c(0, 0, 2, 0))
for(i in 1:4) {
ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
plot(ff, data = anscombe, col = "red", pch = 21, bg = "orange", cex = 1.2,
xlim = c(3, 19), ylim = c(3, 13))
abline(mods[[i]], col = "blue")
}
mtext("Anscombe's 4 Regression data sets", outer = TRUE, cex = 1.5)
par(op)
>>107
�������[�����}����ɂ�
N=1e3
Fer=NULL
for(i in 1:N){
for(j in i:N){
if(f(c(i,j))>0) Fer=rbind(Fer,c(i,j))
}
}
Fer
�����A�������x��������ȁB �C�����C���N�푈�̂��ƃC���N�ɘ��S�����Ƃ��ăt�Z�C��������������̂�CIA
�����悤�ɔs�����{�Ɏ����}�Ƃ������S������CIA�������
CIA��A����Ƃ̎��ʗ_�m�v�ƊݐM��ɖڂ�����
�����}��������̂͏����|�Վ��R�}�Ɣ��R��Y����}
���̏����̌�p�҂ƂȂ莩���}���قƂȂ�60�N���Ĉ��ۂ���������
������CIA�H����A�݁A���R�𑍍قɂ������ʗ_�m�v��CIA�H����A
�ݐM�CIA�H����A�����h�쁨CIA�H����A�ǔ��I�[�i�[���͏����Y��CIA�H���
�������Ď����}��1958�N����CIA�����7000���`1���~(���݂�10���~)�̎������\�����萭�E�H�������55�N�̐����ێ�����
50�N�o�߂��A�����J�����J�@�ɂ��2007�NCIA����̎�����R�[�h�l�[���Ȃǂ����炩�ƂȂ���
����ł��A�����J�̈ӌ��ɋt�炦�ΐ��E���玸�r����
�c���p�h�⏬���Y��������
>>124
�S���܂ł�T�����������ʂ�
[,1] [,2]
[1,] 70 212
[2,] 700 2120 >>124
�����Ɏ��Ԃ������邩��A�r���o�߂�\������悤�ɂ������������ȁB
N=1e3
Fer=NULL
for(i in 1:N){
for(j in i:N){
if(f(c(i,j))>0){
Fer=rbind(Fer,c(i,j))
print(Fer)
}
}
}
Fer A����E��5�l�͂��ꂼ�ꐳ���҂��R���̂ǂ��炩�ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
�R���Ȃ�K���R�����B�R���̉\��������̂͒N���H
A�uB�͐����҂ł���v
B�uA�͐����҂ł���v
C�uB���R���Ȃ玄���R���ł���v
D�uC�������Ȃ玄�������ł���v
E�uD���R���Ȃ玄���R���ł��邵�AD���������̂Ȃ玄�������҂ł���v
�n���́A���ȂȂ��Ꭱ��Ȃ��@�́@�ҋ����@�n��������Ύ���ł���@�Ɠ�����̂��h��ӃV���c�ゾ����
>128�ɐ����ł��Ȃ����낤�ȁB�@�h��ӓ��]�̍������������悤�Ȃ��̂����B
�n���́A���ȂȂ��Ꭱ��Ȃ��@�́@����@�n��������Ύ���ł���@�Ɠ�����̂��h��ӃV���c�ゾ����
>128�ɐ����ł��Ȃ����낤�ȁB�@�h��ӓ��]�̍������������悤�Ȃ��̂����B
���Z���w�����낢���Hw
�����̈Ⴄ�������w�S�}���Ƃ��邼
���ق�남�܂�
�\��������ł����������炵���ȁB
"
A����E��5�l�̒��ɐ����҂ƉR���̑o��������Ƃ킩���Ă���B
�N�������҂��R�����͂��݂��ɒm���Ă���B
�R���Ȃ�K���R�����B�R����S������B
A�uB�͐����҂ł���v
B�uA�͐����҂ł���v
C�uB���R���Ȃ玄���R���ł���v
D�uC�������Ȃ玄�������ł���v
E�uD���R���Ȃ玄���R���ł��邵�AD���������̂Ȃ玄�������҂ł���v
"
>>131
���Ⴀ�A��w���{���x���̖��ɓ����Ă݁I
����̓V���c����Ӎ������]�ɂ͖������낤�ȁB
�h��ӃV���c���������c��100�l���������������B
���������l�������̂܂܌��\�̓��o�����錋�ʂł��������߁A
�A�����ė������݂������ő吔��4�l�ł������Ƃ������\�����B
���\���ʂ��������Ƃ��ė������w�l���̊��Ғl�A�ŕp�l�A�y��95%�M����Ԃ��q�ׂ�B �Տ���w�͊m�����ۂ������B
�����f�[�^����f�肷��̂̓A�z�B
�M����Ԃ�ݒ肵�ċc�_����̂��Տ���̐������p�B
���ꓚ���Ă݁B���Z���w�̒m���ł͐M����ԎZ�o�͖����B
�h��ӃV���c��ɂ����R�A�����B
�h��ӃV���c���ɂ���N�̗����[���ۑ�����Ă��邱�Ƃ����������B
�����͂P�O�O�O���ȉ��ł��邱�Ƃ͔������Ă��邪�A���̐��𐄒肵�����B
�������w������������ׂɂP�O���I��Ŕԍ����L�^���Č��ɖ߂����B
�ʂ̗������w������������ׂɂQ�O���I��Ŕԍ����L�^�����B
��l�̒������̋L�^�����ԍ����ƍ�����ƂR���̔ԍ�����v���Ă����B
���̏�炱�̔N�̗����̐��̍ŕp�l�A���Ғl�Ƃ��̂X�T���M����Ԃ����߂�B
>>66
A�Ɖ~�̒��S�ƑΏ̂ƂȂ�_���A�ڎw���ď�ɕ����]������Ƃ������j�ŁA�葬�ō�}���Ă݂��B
�Ίp���g���������y�������B���l�ϕ���g�ݍ��ނ͔���B

B�̋Ȑ��̐ڐ��Ɖ~���̌�_�����̎��_�ł�A�ƑΏ̂ɂȂ��Ă���i�͂��j�B
�}��A�̑��x��B�̂P�D�Q�{�̂Ƃ��B >>131
�ʂɎ��p��K�v�Ȑ��l������������B�s��ϕ���萔�l�ϕ��B
����A�v�Z�ł���H
�ЊQ���������Ă�����Ƃ���ɏd�ǔ�Ў҂�����
���h������o�����ċ~�}�Z���^�[�Ɋ��҂��������
���h������~�}�Z���^�[�ւ̋�����100km
�~�}�Ԃ̃K�\������50L�A���҂��悹�Ȃ���Ԃł͔R���10km/L
���҂��悹�Ă̔R��͂Tkm/L�ł���
���҂��~����n��̖ʐς͂�����ɂȂ邩�H �����������̈Ӗ������w���ɂł��킩��悤�ȕ�������B
���̓v���O�������ĉ��������ǍŒZ���Ȃ̂��m�M�����Ă�B
��� : 11 ���b�g���� 7 ���b�g���̗e����g���� 9 ���b�g���̐��𑪂�ɂ͂ǂ���������H
������13���Ɠ����������߁B
�T�e���C�g�A�s�����̃X�e�[�L�n�E�X�ŐH�����ċx�������ƁB
�R�����̓u�[���㐔�g�����v���O�����g�����y���ƕ��������̂͐Q�����ł̎��l�������ȁB
>>132
�_����ς����A�v���O�������i�j�̑Ή��ō����������B
n=5
TE=gtools::permutations(2,n,v=0:1,rep=T) # TE : ��P�s��00000 �Ŏn�܂�ŏI�s��11111�ŏI���s��
colnames(TE)=LETTERS[1:n]�@# �e��̖��OA~E
fn <- function(x){
if(sum(x)==n|sum(x)==0) return(FALSE)
cond <- function(P,Q) !(P & !Q) # P �� Q�̐^�U��Ԃ���
all(c( # all : c()���� , �ŋ��ꂽ���肪�S�Đ�������TRUE/FALSE�ŕԂ�
# c(A�������҂ŏ،���������|A���R���ŏ،����R, B�������҂ŏ،���������|B���R���ŏ،����R, ...)
(x[1]==1 & x[2]==1) | (x[1]==0 & x[2]==0),
(x[2]==1 & x[1]==1 ) | (x[2]==0 & x[1]==0),
(x[3]==1 & cond(x[2]==0,x[3]==0)) | (x[3]==0 & !cond(x[2]==0,x[3]==0)),
(x[4]==1 & cond(x[3]==1,x[4]==1)) | (x[4]==0 & !cond(x[3]==1,x[4]==1)),
(x[5]==1 & (cond(x[4]==0,x[5]==0)|cond(x[4]==1,x[5]==1)) )
| �@(x[5]==0 & !(cond(x[4]==0,x[5]==0) | cond(x[4]==1,x[5]==1)) )
))
}
TE[apply(TE,1,fn),] # �e�s��foo��K�p���ĕԂ�l��TRUE�̂��̂�\�� �璷�ȋL�q�l�̖���ɕύX
n=5
TE=gtools::permutations(2,n,v=0:1,rep=T) # TE : ��P�s��00000 �Ŏn�܂�ŏI�s��11111�ŏI���s��
colnames(TE)=LETTERS[1:n]�@# �e��̖��OA~E
fn <- function(x){
if(sum(x)==n|sum(x)==0) return(FALSE)
cond <- function(P,Q) !(P & !Q) # P �� Q�̐^�U��Ԃ���
all(c( # all : c()���� , �ŋ��ꂽ���肪�S�Đ�������TRUE/FALSE�ŕԂ�
# c(A�������҂ŏ،���������|A���R���ŏ،����R, B�������҂ŏ،���������|B���R���ŏ،����R, ...)
(x[1]==1 & x[2]==1) | (x[1]==0 & x[2]==0),
(x[2]==1 & x[1]==1 ) | (x[2]==0 & x[1]==0),
(x[3]==1 & cond(x[2]==0,x[3]==0)) | (x[3]==0 & !cond(x[2]==0,x[3]==0)),
(x[4]==1 & cond(x[3]==1,x[4]==1)) | (x[4]==0 & !cond(x[3]==1,x[4]==1)),
(x[5]==1 & (x[4]==x[5]) ) | (x[5]==0 & (x[4]!=x[5]) )
))
}
TE[apply(TE,1,fn),] # �e�s��fn��K�p���ĕԂ�l��TRUE�̂��̂�\��
arg <- function(z) ifelse(Arg(z)<0,Arg(z)+2*pi,Arg(z))
arg(-1i)/pi
arg(1i)/pi
arg <- function(z) ifelse(Arg(z)<0,Arg(z)+2*pi,Arg(z))
arg(-1i)/pi
arg(1i)/pi
iArg <- function(B,A) arg(B)-arg(A) < pi # increase Arg?
iArg(-1+1i,2+1i)
iArg(-1-1i,2+1i)
sign���g���ƋL�q���ȗ����ł���B
iArg <- function(B,A){ # increase Arg?
d=arg(B)-arg(A)
ifelse(abs(d)<pi, sign(d),-sign(d))
}
iArg(1i,1)
iArg(1,1i)
iArg(1,-1i)
iArg(-1i,1)
"1�`5�̎��R���������ꂽ5���̃J�[�h���AA�`E�̐��k5�l�ɐ搶��1�����z�����B
5�l�͂��ꂼ�ꎩ���̃J�[�h�̐��͕����邪�A���̐l�̃J�[�h�̐��͂킩��Ȃ��B
�܂��A�搶�͒N�̐����킩��Ȃ��B
���āA�搶��A�`E�Ƃ̊ԂŎ��̂悤�ȉ�b���������B
�Ȃ��A�S�������҂ł���A�ォ�瓚����l�͐�̉�b���ĎQ�l�ɂ��Ă���B
�搶�uA����A�N��1�ԑ傫�����ł����H�v
A�u�킩��܂���v
�搶�uB����A���Ȃ���C��������傫�����ł����H�v
B�u�킩��܂���v
�搶�uC����A���Ȃ���D��������傫�����ł����H�v
C�u�킩��܂���v
�搶�uD����A���Ȃ���B��������傫�����ł����H�v
D�u�����������v
�搶�uB����A���Ȃ���C��������傫�����ł����H�v
B�u�������v
�搶�u���������A�F����̐����킩��܂����v
��1�A�����������ɓ��錾�t�́u�͂��v�u�������v�u�킩��܂���v�̂ǂꂩ�H
��2�AA�`E�̐��͉����H"
>>146
�v���O�����ɂ���@�A�ꍇ����������ȁB
pm=gtools::permutations(5,5)
Yes <- function(x){
all(c(
x[1]!=5,
x[2] %in% 2:4,
x[3] %in% 2:4,
x[4]==4,
x[2]<x[3]
))
}
pm[apply(pm,1,Yes),]
No <- function(x){
all(c(
x[1]!=5,
x[2] %in% 2:4,
x[3] %in% 2:4,
x[4]==2,
x[2]<x[3]
))
}
pm[apply(pm,1,No),] DK <- function(x){
all(c(
x[1]!=5,
x[2] %in% 2:4,
x[3] %in% 2:4,
x[4]==3,
x[2]<x[3]
))
}
pm[apply(pm,1,DK),]
�I�����s�b�N�T�C�Y�E�v�[��50m�~25m�̐��̓������v�[���̈�̊p�ɊĎ�����u���B
���̊Ď����͐��E�L�^�ňړ�������̂Ƃ���B
���j100m���R�` 46�b91�Ő������ړ�
����100m9�b58�Ńv�[���T�C�h���v�ړ�
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b�K�v���v�Z����B
hnr <- function(FUN,lo,up,n=100,maximum==FALSE,prec=1e-5){
xx=seq(lo,up,length=n)
by=(up-lo)/(n-1)
y=sapply(xx,FUN)
z=ifelse(maximum,max(y),min(y))
while(by>prec){
by=by/10
xx=seq(z-by,z+by,by)
y=sapply(xx,FUN)
z=ifelse(maximum,max(y),min(y))
}
}
���w�͎G�ȓ��e����Ƒ��U�œ˂����݂�����B
http://2chb.net/r/math/1572866819/809
��̗���グ�ďڏq������[�����ꂽ�B
>151�͐����̎菇���������Ă݂��B
hnr �͐l�ԃj���[�g�����X�\�����疽���B
�h��ӓ��]����ăv���O�����g�߂Ȃ��́H
���ǂ����w���ł��ł��邯�ǁB # under construction
hnr <- function(FUN,lo,up,n=100,maximum=FALSE,prec=1e-5){
xx=seq(lo,up,length=n)
by=(up-lo)/(n-1)
y=sapply(xx,FUN)
z=ifelse(maximum,max(y),min(y))
while(by>prec){
by=by/10
xx=seq(z-by,z+by,by)
y=sapply(xx,FUN)
z=ifelse(maximum,max(y),min(y))
}
return(z)
}
>>153
�H���I��
rm(list=ls())
graphics.off()
# ���̋ɑ�ɏ��l��Ԃ�local maximum and minimum
# FUN:�� lo:�͈͉��� up:�͈͏�� n:�͈͕����� prec:���x
lmm <- function(FUN,lo,up,n=100,maximum=FALSE,prec=1e-7,print=TRUE){
xx=seq(lo,up,length=n) # �͈͂�n�̐��l�ɕ���
by=(up-lo)/(n-1) # by:���������v�Z
y=sapply(xx,FUN) # xx�Ŏ��s����
if(print) plot(xx,y,bty='l',type='l') # �����l�͈͂̊���`��
z=ifelse(maximum,max(y),min(y)) # �ɑ�l/�ɏ��l z�ׂ�
x=xx[which(y==z)]# x�ɋɒl��^�����ϐ��̒l��Ԃ�
while(by>prec){ # �����������x���傫������
xx=seq(x-by,x+by,length=n) # x�𒆐S��[x-by,x+by]�Ŏ��s
y=sapply(xx,FUN)
z=ifelse(maximum,max(y),min(y))
x=xx[min(which(y==z))] # ���ɒl��^�����ϐ��l�̏�������
by=by/10 # ����͕�����by��1/10�ɂ��Ď��s
}
re=c(value=z,at=xx[min(which(y==z))]) # �ϐ���at�̂Ƃ��ɋɒlvalue��re�ɂ����
return(round(re,-log10(prec))) # ���x�ɉ��������ŕԂ�
}
lmm(function(x) sin(x)+cos(x),-pi,pi,max=F)
lmm(function(x) x^3-6*x^2+10,-2,3,max=TRUE) ����
cos��+sin�Ƃ̍ő�l�ƍŏ��l�����߂�
> lmm(function(x) sin(x)+cos(x),-pi,pi,max=T)
value at
1.4142136 0.7853981
> lmm(function(x) sin(x)+cos(x),-pi,pi,max=F)
value at
-1.4142136 -2.3561945
���p�ɑς��鐸�x���o���I
> options(digits=22)
> f=function(x) cos(x)+sin(x)
> lmm(f,-pi,pi,maximum=TRUE,prec=1e-16)
value at
1.41421356237309515 0.78539815960067616
> opt=optimise(f,c(-pi,pi),maximum=TRUE,tol=1e-7) ; c(opt[[2]],opt[[1]])
[1] 1.41421356237309492 0.78539816341094015
> c(f(pi/4), pi/4)
[1] 1.41421356237309492 0.78539816339744828
Wolfram
1.414213562373095048801688724209698078569671875376948073176...
0.785398163397448309615660845819875721049292349843776455243...
>>158
�h��ӓ��]����ăv���O�����g�߂Ȃ��́H
���ǂ����w���ł��ł��邯�ǁB ���������̂��ėc�t�����ł����̈Ӗ��͂킩��Ǝv����ˁB
A����E��5�l�̒��ɐ����҂ƉR���̑o��������Ƃ킩���Ă���B
�N�������҂��R�����͂��݂��ɒm���Ă���B
�R���Ȃ�K���R�����B�R����S������B
A�uB�͐����҂ł���v
B�uA�͐����҂ł���v
C�uB���R���Ȃ玄���R���ł���v
D�uC�������Ȃ玄�������ł���v
E�uD���R���Ȃ玄���R���ł��邵�AD���������̂Ȃ玄�������҂ł���v
�����̐����̉��x��7��
65���̂�����98���̓����g����500��L��肽���B
yu = function(V=500,T=65,C=7,H=98) V*(T-C)/(H-C)
yu()
�����͂��Ȃ�̖�ł��邾��
�f�p�X�n���V�I���͒m��Ȃ�����
>>161
���Ă̓V���c���ȁB
�H�ł͂��邪�A���Ì��ʂ����҂ł���F�m�ǂ��Ă����ˁB
���툳�����ǂƂ������d��������Ƃ��B ���܂�V���c���]�ł�������w�ɓ��w�ł��鎞��ȂȂ��B
�J���S�J�����o�g��앟���m����Ă܂��B
���͊֓��ɍݏZ���Ă܂��B��҂̂Ȃ肽�������ł�
�������̓����s���A�O���ȏȋǒ��̑��q�������̂ɁA
��ȑ�w�����ȏȂ̊NJ��ł���Ƃ����펯���猇���Ă���悤�ȃA�z���������w����̂��h��ӃV���c���B
�J���͉��ɂ��Ȃ��_�T�������@����ϓ���������
����ɂ��Ă����̐l�B�͂悭���ׂ���ȁB���[�䂤�l�B���{���̓��̗ǂ��l�Ȃ�
��͂��҂�{�点����|����ȁ@�͎����Ă邵
�����ĉR�����Ȃ����q�吶����u���Ȃ��̂������Ƃ��Ԉ���Ă��Ȃ���Ύ�R�L���A�t�F�������Ă�����v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
>>174
�h��ӃV���c��͓��ɂ����݂������ˁB
��ӎ�����呲��������w��w������i�ރX�� [�]�ڋ֎~](c)2ch.net
http://2chb.net/r/hosp/1424846816/695
695 ���O�F���̖���������[] ���e���F2016/09/25(��) 22:04:25.53 ID:FzuOCpqV
�����搶
���_��
��
1
�]��
�����o�ł��A�f���炵����t�����邵�A�����ł��A�ǂ����悤���Ȃ��̂�����B
����Ȃ̂́A�����܂Ōl�̎������Ǝv���Ă܂����B
���A
������a�@�i��t�̑啔�����A�������ӎ����j�ɗ��āA���̍l���͕ς��܂����B
�Ƃ���A�C�ɐH��Ȃ���t�̔��߂�T���_�����B���A���̏�ɃS�~��u���A�ȂǁA���w�����݂������点�����Ă����t�Ƃ����̂��A�͂��߂Č��܂����B
�����o�̕ϐl�����X�݂Ă��܂������A����ȁA���w���̃C�^�Y���݂����Ȃ��Ƃ�����l�́A���܂���ł����B
��͂�A��ӎ����́A����Ȃ�ȂƎv���܂����B
2016�N09��02�� 00��21��09�b >>177
�t�F�����Ă��炤�ɂ͉��ƌ��������H ��ʏ펯��m��Ȃ��l���a�@�g�D�ŏ�肭������邱�Ƃ͂ł��Ȃ�����w�l�ԊW�̃X�g���X���Ȃ��o�C�g�ł����Ȃ���w�܂��͈�҂ɂȂ��Ă��炾��w���A��҂ɂȂ�͖̂�����w
>>179
�t�F�����Ă��炤�ɂ͉��ƌ��������H
���q�吶�Ƀt�F�����Ă���������ƂȂ��́H �t�F���ɂ͋������Ȃ��̂��H
����A�P�ɓ������������Ȃ낤�ȁB
���̃X���ɍ��킹�Ă݂��B
�����O�Ɋ�t�������h��ӃV���c���̐e��
��t�������Ƃ��ĕs���i�ɂȂ�̂łȂ����ƐS�z���ė������ƒk�������Ƃ���A���i�Ɗ�t���͕s���ł���A
���q�l���ʐڂŐ������咣�������
��t���ԋp��
�������i�ɂȂ�
�ƌ���ꂽ�B
�������͉R�����Ȃ��B
�������w�������h��ӃV���c���͖ʐڂłȂ�Ǝ咣����悢���H
����ɓ����o�����ɓ��������ăh��ӈ�̓t�F���������A���������낤�Ȃ��B
�����ĉR�����Ȃ����q�吶����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
���̕�������ɂ����Ă邩���ȁB
���i�Ɗ�t���͕s�����f����h��ӈ��ɓ����O�Ɋ�t���������̐e����t�������Ƃ��ĕs���i�ɂȂ�̂łȂ����ƐS�z���ė������ƒk�������B
���i�Ɗ�t���͕s���Ƃ�����w�̕��j�͏�ɐ��������A�������͏�ɉR�����B
�k���ł́A
�u���q�l���ʐڂŐ������咣������Ί�t���ԋp���������i�ɂȂ�A�Ԉ�����咣�ł���Ί�t���v���ŕs���i�ɂȂ�v
�ƌ���ꂽ�B
�������w�������h��ӃV���c���͖ʐڂłȂ�Ǝ咣����悢���H
�ʁiP��Q�@�ȁ@��P�ˁ�Q�j
�ʁiP��Q�j�� �ʁi��P�ˁ�Q�jwhere P��Q�@�߁@�ʁiP�ȁ�Q�j
�ʁʁiP�ȁ�Q�j�� �ʁʁi��P�ȁʁ�Q�j
�iP�ȁ�Q�j�� �i��P��Q
�ʁiP��Q�@�ȁ@��P�ˁ�Q�j
�ʁiP��Q�j�� �ʁi��P�ˁ�Q�jwhere P��Q�@�߁@�ʁiP�ȁ�Q�j
�ʁʁiP�ȁ�Q�j�� �ʁʁi��P�ȁʁ�Q�j
�iP�ȁ�Q�j�� �i��P��Q�j
>>186
�����������ɂ���Ə�������Ȃ�ȁB�������ł��h��ӓ��]�ɂ͖����Ǝv���B
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H �j���[���{�ɂ��������ӌ���
49 ���������P���N 2020/01/23(��) 06:28:26.69 ID:fsvBnYrD0
�������͂ǂ��ł������B
���ň�҂ɂȂ�Ƃ��낾��B
# https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14116594724
"
�U�l�W�܂�ƁA���̒��Ɂu�݂��ɒm�荇���̂R�l�����݂���v���A�܂��́A�u�݂��ɒm�荇���łȂ��R�l�����݂���v���Ƃ������B
"
rm(list=ls())
c2=gtools::combinations(6,2) # 6�l��2�l�I�ԑg�ݍ��킹�@15�ʂ�
p15=gtools::permutations(2,15,0:1,re=T) #�@15�ʂ肪�m�荇��(1)���ہi�O�j���@2^15�ʂ�
c3=gtools::combinations(6,3) ; # 6�l����3�l��I�ԑg�ݍ��킹 20�ʂ�
ramsey <- function(x){
(acq=c2[x==1,]) # �m�荇���̑g�ݍ��킹
if(is.null(nrow(acq))) acq=t(as.matrix(acq))
is3acq=FALSE
nr=nrow(c3)
for(i in 1:nr){
j1=which(c3[i,1] == acq[,1]) # c3�̑g�ݍ��킹��1�l�ڂ�1��ڂ�index��Ԃ�
j2=which(c3[i,2] == acq[,1])
j3=which(c3[i,3] == acq[,1])
aq1=acq[c(j1,j2,j3),2] # 1��ڂ̒m�荇��
j1=which(c3[i,1] == acq[,2]) # c3�̑g�ݍ��킹��1�l�ڂ�2��ڂ�index��Ԃ�
j2=which(c3[i,2] == acq[,2])
j3=which(c3[i,3] == acq[,2])
aq2=acq[c(j1,j2,j3),1] # 2��ڂ̒m�荇��
su=sort(unique(c(aq1,aq2)))�@# �d���������ă\�[�g
is3acq=all(c3[i,] %in% su) # �݂��ɒm�荇������Ԃ�
if(is3acq) break
}
if(is3acq) return(1) (acq=c2[x==0,]) # ���l�̑g�ݍ��킹
if(is.null(nrow(acq))) acq=t(as.matrix(acq))
is3acq=FALSE
nr=nrow(c3)
for(i in 1:nr){
j1=which(c3[i,1] == acq[,1]) # c3�̑g�ݍ��킹��1�l�ڂ�1��ڂ�index��Ԃ�
j2=which(c3[i,2] == acq[,1]) #
j3=which(c3[i,3] == acq[,1]) #
aq1=acq[c(j1,j2,j3),2] # 1��ڂ̑��l
j1=which(c3[i,1] == acq[,2]) # c3�̑g�ݍ��킹��1�l�ڂ�2��ڂ�index��Ԃ�
j2=which(c3[i,2] == acq[,2]) #
j3=which(c3[i,3] == acq[,2]) #
aq2=acq[c(j1,j2,j3),1] # 2��ڂ̑��l
su=sort(unique(c(aq1,aq2))) # �d���������ă\�[�g
is3acq=all(c3[i,] %in% su) # �݂��ɑ��l����Ԃ�
if(is3acq) break
}
if(is3acq) return(-1)
return(0)
}
sum(apply(p15,1,ramsey)==0)
>>187
���w�ɑ�ނ�ς��ē��e�����瑬�U�Ő����������Ȃ��B ���͉ߋ����������邱�Ƃł͂���܂���B
���悤�Ȃ��Ƃ��ł���킯�͂���܂���B
��ɂȂ��ĉߋ���ς�����A
�N����Ȃ��������Ƃɂ���킯�ɂ͂܂���܂���B
�������ߋ��ɖڂ�����҂͌��ǂ̂Ƃ��댻�݂ɂ��ӖڂƂȂ�܂��B(���@�C�c�[�b�J�[)

���җl����̂��肪���������t�ł��B
>>
�c��ȏ������p���Ȃ�������Ȃ��d�����ƔF�����Ă��邩�炱���A���̂��������a�C�ɂ����Ă͓��ɁA���߂Ď������͓��������搶�ɐf�Ă��炢�����Ǝv���Ă��܂��܂��B���̏ꍇ�ɁA�o�g�Z�A���w�����w�Z�A�͉R�����Ȃ��Ƃ������܂��B
<<
>�o�g�Z�A���w�����w�Z�A�͉R�����Ȃ��Ƃ������܂��B
>�o�g�Z�A���w�����w�Z�A�͉R�����Ȃ��Ƃ������܂��B
>�o�g�Z�A���w�����w�Z�A�͉R�����Ȃ��Ƃ������܂��B
��ȋ����Ȃ̂Ł@�J��Ԃ��܂����B
##
"
N(=6)�l�W�܂�ƁA���̒��Ɂu�݂��ɒm�荇����M(=3)�l�����݂���v���A�܂��́A
�u�݂��ɒm�荇���łȂ�M�l�����݂���v���Ƃ������B
"
rm(list=ls())
N=6;M=3
(cN2=gtools::combinations(N,2)) # N�l��2�l�I�ԑg�ݍ��킹 choose(N,2)(=15)�ʂ�
N2=nrow(cN2)
pN=gtools::permutations(2,N2,0:1,re=T) #�@N2�ʂ肪�m�荇��(1)���ہi�O�j���@2^N2�ʂ�
(cNM=gtools::combinations(N,M)) ; # N�l����M�l��I�ԑg�ݍ��킹 choose(N,M)(=20)�ʂ�
(x=pN[10000,])
(x=pN[1,])
ramsey <- function(x){
(acq=cN2[x==1,]) # �m�荇���̑g�ݍ��킹
if(is.null(nrow(acq))) acq=t(as.matrix(acq))
is3acq=FALSE
J=NULL
nr=nrow(cNM)
for(i in 1:nr){
for(j in 1:M){
J=c(J,which(cNM[i,j]==acq[,1])) # cN2�̑g�ݍ��킹��j�l�ڂ�1��ڂ�index��Ԃ�
}
aq1=acq[J,2] # 1��ڂ̒m�荇��
for(j in 1:M){
J=c(J,which(cNM[i,j]==acq[,2])) # cN2�̑g�ݍ��킹��j�l�ڂ�2��ڂ�index��Ԃ�
}
aq2=acq[J,1] # 2��ڂ̒m�荇��
su=sort(unique(c(aq1,aq2)))�@# �d���������ă\�[�g
is3acq=all(cNM[i,] %in% su) # �݂��ɒm�荇������Ԃ�
if(is3acq) break
}
if(is3acq) return(1)
(acq=cN2[x==0,]) # ���l�̑g�ݍ��킹
if(is.null(nrow(acq))) acq=t(as.matrix(acq))
is3acq=FALSE
J=NULL
nr=nrow(cNM)
for(i in 1:nr){
for(j in 1:M){
J=c(J,which(cNM[i,j]==acq[,1])) # cN2�̑g�ݍ��킹��j�l�ڂ�1��ڂ�index��Ԃ�
}
aq1=acq[J,2] # 1��ڂ̒m�荇��
for(j in 1:M){
J=c(J,which(cNM[i,j]==acq[,2])) # cN2�̑g�ݍ��킹��j�l�ڂ�2��ڂ�index��Ԃ�
}
aq2=acq[J,1] # 2��ڂ̒m�荇��
su=sort(unique(c(aq1,aq2)))�@# �d���������ă\�[�g
is3acq=all(cNM[i,] %in% su) # �݂��ɒm�荇������Ԃ�
if(is3acq) break
}
if(is3acq) return(-1)
return(0)
}
sum(apply(pN,1,ramsey)==0)
��ʉ����ď����������̂łS�l�ł��������邱�Ƃ��m�F�ł����B
"A�`D��4�l���������̌��ʂɂ��āA4�l�͂��ꂼ��ȉ��̂悤�ɏq�ׂĂ��邪�A
�{���̂��Ƃ��q�ׂĂ���̂�1�l�����ŁA����3�l�͂��ׂĂ������q�ׂĂ���B
���i�����̂�2�l�ł���Ƃ��A���i����2�l�Ɛ����҂͒N���B
A�@B�͍��i�����B
B�@A��C�̂���1�l���������i�����B
C�@B�������Ă��邱�Ƃ͐������B
D�@C�������Ă��邱�Ƃ͂����ł���B
"
TE=gtools::permutations(2,8,0:1,re=T)
f <- function(x){
if(sum(x[1:4])!=1 | sum(x[5:8])!=2) return(FALSE)
else{
all(c(
x[1]==1 & x[6]==1 | x[1]==0 & x[6]==0,
x[2]==1 & sum(x[c(5,7)])==1 | x[2]==0 & sum(x[c(5,7)])!=1,
x[3]==1 & x[2]==1 | x[3]==0 & x[2]==0,
x[4]==1 & x[3]==0 | x[4]==0 & x[3]==1
))
}
}
colnames(TE)=c(LETTERS[1:4],letters[1:4])
head(TE) # A~D:honest(1) or liar(0), a~d:success(1) or failure(0)
TE[apply(TE,1,f),]
> TE[apply(TE,1,f),]
A B C D a b c d
0 0 0 1 1 0 1 0
"�`�C�a�C�b�C�c�̂S�l���}���\�����������܂����B���̂Ƃ��̏��ʂɂ��āA
�S�l�͂��ꂼ�ꎟ�̂悤�Ɍ����Ă��܂����A�P�l�������������Ă��܂��B�S�l�̐��������ʂ��Ȃ����B�������A���ʂ͂S�l�Ƃ��قȂ���̂Ƃ��܂��B
�@�@�`�N�F�u���́A�Q�ʂł��S�ʂł��Ȃ��v
�@�@�a�N�F�u���́A�P�ʂ������v
�@�@�b�N�F�u���́A�`�N��葬�������v
�@�@�c�N�F�u���́A�S�ʂ������v
"
TE=gtools::permutations(4,4)
f <- function(x){
sum(c(
x[1]!=2 & x[1]!=4,
x[2]==1,
x[3]<x[1],
x[4]==4
))
}
TE[apply(TE,1,f)==3,]
> TE[apply(TE,1,f)==3,]
[1] 3 2 1 4
A, B�AC�͗�����A���K��A�F�m�NJ��҂���Ȃ邪�O���ŋ�ʂł��Ȃ��B
������͏�ɉR�����A���K��͏�ɐ^�������A�F�m�NJ��҂͉R���^�������B
A�@�uB�͔F�m�NJ��҂ł��v
B�@�uC�͗����ł͂���܂���v
C�@�uA�͔F�m�NJ��҂ł͂���܂���v
A�AB�AC�͒N������B
TE=gtools::permutations(3,3,-1:1)
f <- function(x){
all(c(
x[1]==1 & x[2]==0 | x[1]==-1 & x[2]!=0 | x[1]==0,
x[2]==1 & x[3]!=-1 | x[2]==-1 & x[3]==-1 | x[2]==0,
x[3]==1 & x[1]!=0 | x[3]==-1 & x[1]==0 | x[3]==0
))
}
TE[apply(TE,1,f),]
����c�t���ŁA����ŗV��ł���A,B,C,D �����ŗV��ł���E,F,G�̂V�l�̒��ɁA�t�オ�肪�ł���q���Q�l���邱�Ƃ��������Ă���B
�����ŁAA�`G�ɐq�˂��Ƃ���A���ꂼ��ȉ��̔����������B
�������A�V�l�����A�{���̂��Ƃ������Ă���̂͂Q�l�����ŁA���Ƃ̂T�l�͊Ԉ�������Ƃ������Ă����B�����̂��Ƃ���m���ɂ�����̂͂ǂꂩ�B
A�FB�͋t�オ��ł����B
B�FA�͊Ԉ�������Ƃ������Ă����B
C�FA��B���Q�l�Ƃ��Ԉ�������Ƃ������Ă����B
D�F����ŗV��ł����q�̒��ɂ͋t�オ��ł���q�͂��Ȃ���B
E�F���͋t�オ��ł��Ȃ��B
F�F�t�オ�肪�ł���̂͂Q�l�Ƃ�����ŗV��ł����q����B
G�FE��F�̏��Ȃ��Ƃ��ǂ������͖{���̂��ƌ����Ă����B
f <- function(x){
x1=x[1] ; x2=x[2]
re=rep(0,7)
re[x1]=1; re[x2]=1
re
}
(cmb=t(combn(7,2,f)))
gr=as.matrix(expand.grid(1:21,1:21)) ; head(gr)
g <- function(ij){
i=ij[1] ; j=ij[2]
c(cmb[i,],cmb[j,])
}
TE=t(apply(gr,1,g)) ; tail(TE)
>>204
���ɉ����Ă��������s��������v���O������g�ނ̂�������Ɠ���ȁB
> tail(TE)
A B C D E F G a b c d e f g
[436,] 0 0 0 1 1 0 0 0 0 0 0 0 1 1
[437,] 0 0 0 1 0 1 0 0 0 0 0 0 1 1
[438,] 0 0 0 1 0 0 1 0 0 0 0 0 1 1
[439,] 0 0 0 0 1 1 0 0 0 0 0 0 1 1
[440,] 0 0 0 0 1 0 1 0 0 0 0 0 1 1
[441,] 0 0 0 0 0 1 1 0 0 0 0 0 1 1 ����
1.�{���̂��Ƃ������Ă���́A�P�l�͍���ŗV��ł����q�ł���A�P�l�͕����ŗV��ł����q�ł���B
2.D�͖{���̂��Ƃ������Ă���AE�͊Ԉ�������Ƃ������Ă���B
3.B�͋t�オ�肪�ł��A�Ԉ�������Ƃ͌����Ă��Ȃ��B
4.�t�オ��ł���̂́AF��G��2�l�ł���B
5.�t�オ��ł���̂́A�P�l�͍���ŗV��ł����q�ł���A�P�l�͕����ŗV��ł����q�ł���B
�v���O��������
> TE[apply(TE,1,h),]�@# A-G:����1�R��0 a-g:�t�オ��\1�s�\0
A B C D E F G a b c d e f g
[1,] 0 1 0 1 0 0 0 0 0 0 0 1 1 0
[2,] 0 1 0 1 0 0 0 0 0 0 0 1 0 1
����Đ������̂͂Q
>>204
�����������̖��炵���ȁB��t�����̕����i�i�ɈՂ����ˁB
����������������ė������w�̊w����r����������̂ɁB "
A�`F�̂U�l��100�������������B
�����ʂ̎҂͂Ȃ��A���ꂼ��ȉ��̂悤�ɏq�ׂĂ��邪�A
�^�����q�ׂĂ���̂͂P�ʂƂU�ʂ̎҂݂̂ł���B
A�F���͂S�ʂł͂Ȃ��B
B�F���͂S�ʂł͂Ȃ��B
C�F����A����ʂł���B
D�F����B����ʂł���B
E�FB�͂P�ʂł���B
F�FB�͂S�ʂł���B
"
jun=gtools::permutations(6,6) ;
colnames(jun)=LETTERS[1:6]
tail(jun)
f <- function(x){
all(c(
(x[1]==1|x[1]==6) & x[1]!=4 | !(x[1]==1|x[1]==6) & x[1]==4,
(x[2]==1|x[2]==6) & x[2]!=4 | !(x[1]==1|x[2]==6) & x[2]==4,
(x[3]==1|x[3]==6) & x[3]<x[1] | !(x[3]==1|x[3]==6) & x[3]>=x[1],
(x[4]==1|x[4]==6) & x[4]<x[2] | !(x[4]==1|x[4]==6) & x[4]>=x[2],
(x[5]==1|x[5]==6) & x[2]==1 | !(x[5]==1|x[5]==6) & x[2]!=1,
(x[6]==1|x[6]==6) & x[2]==4 | !(x[6]==1|x[6]==6) & x[2]!=4)
)}
ans=jun[apply(jun,1,f),]
ans
>>208
> f <- function(x){
+ all(c(
+ (x[1]==1|x[1]==6) & x[1]!=4 | !(x[1]==1|x[1]==6) & x[1]==4,
+ (x[2]==1|x[2]==6) & x[2]!=4 | !(x[2]==1|x[2]==6) & x[2]==4,
+ (x[3]==1|x[3]==6) & x[3]<x[1] | !(x[3]==1|x[3]==6) & x[3]>=x[1],
+ (x[4]==1|x[4]==6) & x[4]<x[2] | !(x[4]==1|x[4]==6) & x[4]>=x[2],
+ (x[5]==1|x[5]==6) & x[2]==1 | !(x[5]==1|x[5]==6) & x[2]!=1,
+ (x[6]==1|x[6]==6) & x[2]==4 | !(x[6]==1|x[6]==6) & x[2]!=4)
+ )}
> ans=jun[apply(jun,1,f),]
> ans
A B C D E F
[1,] 1 4 2 5 3 6
[2,] 1 4 3 5 2 6
[3,] 4 1 5 2 6 3
[4,] 4 1 5 3 6 2
[5,] 4 6 5 1 2 3
[6,] 4 6 5 1 3 2 "
A,B,C,D,E�̂T�l�̒��ɂ�����܂ݐH�������l���R�l���܂��B
������ƁA�T�l�͎��̂悤�ɓ����܂����B
A�@���͐H�ׂ܂����B�ł�E���H�ׂ܂����B
B�@C�͐H�ׂ܂����B�ꏏ��D���H�ׂ܂����B
C�@���͐H�ׂĂ��܂���BB���H�ׂĂ��܂���B
D�@���͂������H�ׂĂ��܂���B�����悤��C���H�ׂĂ��Ȃ��ł���B
E�@���͐H�ׂĂ��܂���B�ł�C�͐H�ׂ܂����B
���ꂼ�ꔼ���͖{���̂��Ƃ������A�����͂����������Ă���Ƃ���ƁA�܂ݐH
���������R�l�͂���ł����B
"
f <- function(x){
x1=x[1] ; x2=x[2] ; x3=x[3]
re=rep(0,5)
re[x1]=1 ; re[x2]=1 ; re[x3]=1
re
}
(TE=t(combn(5,3,f)))
colnames(TE)=LETTERS[1:5]
g <- function(x){
all(c(
x[1]==1 & x[5]==0 | x[1]==0 & x[5]==1,
x[3]==1 & x[4]==0 | x[3]==0 & x[4]==1,
x[3]==0 & x[2]==1 | x[3]==1 & x[2]==0,
x[4]==0 & x[3]==1 | x[4]==1 & x[3]==0,
x[5]==0 & x[3]==0 | x[5]==1 & x[3]==1)
)
}
TE[apply(TE,1,g),]
�p�ɂɎg���e���v���[�g������
TEnr <- function(n,r,one=1){ # n(=5),r(=3)���w�肵�� 0 0 1 1 1����1 1 1 0 0�܂ł̏���s������
f=function(x){
re=numeric(n) # �e��q
re[x]=one # �w���index��one����
re
}
t(combn(n,r,f)) # one������g�ݍ��킹�ɏ�L��f�����s���ē]�u
}
A,B,C��3�l�����āA���ꂼ�ꃊ���S��1��2�����Ă��܂��B
1�����Ă���l�͕K���E�\�����܂����A2�����Ă���l�̓E�\�������ǂ����킩��܂�
��B1�����Ă���l�����Ȃ��Ƃ�1�l����Ƃ��A3�l�����ꂼ�ꎟ�̂悤�Ɍ���
�܂����B
A�@B��C�̃����S�̍��v�͂Q�ł͂���܂���B
B�@A��C�̃����S�̍��v�͂R�ł͂���܂���B
C�@A��B�̃����S�̍��v�͂S�ł͂���܂���B
���̂Ƃ��AA,B,C�������Ă��郊���S�̌��̍��v�ƁA�E�\�����Ă���l�̑g�ݍ��킹�́H
"
TE=gtools::permutations(2,3,re=T)
f <- function(x){
if(sum(x==1)==0){ return(FALSE)
}else{
all(c(
x[1]==1 & sum(x[2:3])==2�@�@|�@x[1]==2,
x[2]==1 & sum(x[c(1,3)])==3 | x[2]==2,
x[3]==1 & sum(x[1:2])==4 | x[3]==2)
)
}
}
TE[apply(TE,1,f),]
>>211
0 1 �ȊO�̏ꍇ�����邩�炱����������������
TEnr <- function(n,r,zero=0,one=1){ # n(=5),r(=3)���w�肵�� 0 0 1 1 1����1 1 1 0 0�܂ł̏���s������
f=function(x){
re=rep(zero,n) # �e��q
re[x]=one # �w���index��one����
re
}
t(combn(n,r,f)) # one������g�ݍ��킹�ɏ�L��f�����s���ē]�u
} "
A�AB�AC�AD�̂S�l�̑̏d�ׂ܂����BB��D�̕��ϑ̏d������2�l�̂ǂ��炩��
�̏d�Ɠ����ŁAA��B���17�s�y���AC��D�Ƃ̑̏d�̍���12�s�ł����B
A�@����C�Ƃ̑̏d�̍���5�s�ł��B
B�@����C�Ƃ̑̏d�̍���22�s�ł��B
C�@���͂S�l�̑̏d�̏��Ԃ�A�̒��O�܂��͒���ł��B
D�@����C���d���ł��B
4�l�̂����A2�l�����������Ă���Ƃ���ƁA�R�������Ă���Q�l�͒N�ł����B
"
>>214
A�̑̏d��50kg�Ƃ��ĉ\�ȑg�ݍ��킹�ŘA���������������đ̏d�̍s���������2�l�R��������s��Ƒg�ݍ��킹�Ċ��Ńt�B���^�[����B
A=50 # �ݒ�l
B=67
C=D+12 | C=D-12
67+D=2*50 (D=33) | 67+D=2*C
w8=rbind(
c(50,67,45,33),
c(50,67,55,43),
c(50,67,11,33),
c(50,67,79,91)
)
(uso=TEnr(4,2))
(gr=as.matrix(expand.grid(1:4,1:6)))
f <- function(i,j){
c(w8[i,],uso[j,])
}
TE=t(mapply(f,gr[,1],gr[,2]))
colnames(TE)=c(LETTERS[1:4],letters[1:4])
g <- function(x){
tf=c(
x[5]==1 & abs(x[1]-x[3])==5 | x[5]==0 & abs(x[1]-x[3])!=5,
x[6]==1 & abs(x[2]-x[3])==22 | x[6]==0 & abs(x[2]-x[3])!=22,
x[7]==1 & abs(which(sort(x)==x[3])-which(sort(x)==x[1]))==1�@|
x[7]==0 & abs(which(sort(x)==x[3])-which(sort(x)==x[1]))!=1,
x[8]==1 & x[4]>x[3] | x[8]==0 & x[4]<=x[3])
all(tf)
}
> TE[apply(TE,1,g),] # A-D:�̏d a-d:����1�R��0
A B C D a b c d
50 67 55 43 1 0 1 0 >>215
����ʔ�������H
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H ���ɕ��������̃}�X�Ɂ��A���A�~�̂����ꂩ�P���L������Ƃ��A�ׂ荇��
���}�X�̏��Ȃ��Ƃ���������ƂȂ�悤�ȋL���̎d�����l���܂��B�Ⴆ�Q��
�}�X�ł���A���}�̂T�ʂ肠��܂��B
�@�@�@�����@�@�����@���~�@�����@�~��
�������݂����悤�ɂV�}�X���L������Ƃ��A���̋L���̎d���͉��ʂ肠�邩�B�@
> sapply(2:13,sim)
[1] 5 11 21 43 85 171 341 683 1365 2731 5461 10923
�J���S�J�����o�g��앟���m�Ł[���@�J���͊����Ł[��
����l����P�z�[�����珇�ɃS���t���v���C���ĉ�����Ƃ���A������̃z�[���̐��т��{�M�[�i�{�P�j�A�_�u���{�M�[�i�{�Q�j���̓g���v���{�M�[�i�{�R�j��
����A����z�[�����I���ăX�R�A�����傤�ǁu�{�V�v�ƂȂ������_�ʼnJ�̂��ߒ��f�����B
���̂Ƃ��A�e�z�[���̐��т̕��т̑g�����͉��ʂ肠�邩�B
�Ȃ��A�{�M�[�A�_�u���{�M�[�A�g���v���{�M�[�Ƃ́A��Ő��������ꂼ��P�ŁA�Q�ŁA�R�ő����ł������т��w���Ă���A��Ő����������ł����Ő���
���a���X�R�A�ł���B�Ⴆ�A��P�z�[������̐��т̕��т��g���v���{�M�[�A�_�u���{�M�[�A�{�M�[�ł������ꍇ�A�X�R�A�́i�{�R�j�{�i�{�Q�j�{�i�{�P�j�Łu�{�U�v�ł���B
�i�@I�@�퍑�ƌ����������̉ߋ���@�j
������̂��ʓ|�Ȃ̂Ńv���O�����ɃJ�E���g������B
for(i in 3:7){
pi=gtools::permutations(3,i,rep=T)
p7=pi[apply(pi,1,sum)==7,]
count[i]=ifelse(is.vector(p7),1,nrow(p7))
}
sum(count)
> sum(count)
[1] 44
>>219
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ��������H >>220
�K�i�o��̏ꍇ�̐��̌v�Z�Ɋ������Ă������B
# ��xi=n xi<=r ��x�ɂ�(=3)�i�܂ŏオ��鎞�A������(=7)�i�オ��ꍇ�̐�
stairway <- function(n,3){
count=numeric(n)
m=ceiling(n/r)
for(i in m:n){
pi=gtools::permutations(r,i,rep=T)
pn=pi[apply(pi,1,sum)==n,]
count[i]=ifelse(is.vector(pn),1,nrow(pn))
}
sum(count)
} �P�R�i�̊K�i����邳���A�P�i��邩�A�Q�i��邩�A�R�i��邩�̂����ꂩ��g���킹�ď�邱
�ƂƂ���B�����͉��ʂ肠�邩�B
> stairway(13,3)
[1] 1705
�����A�h��ӁB
�����o���ăJ�E���g���Ă���B
�I�}�G�̒�ӓ��]�ł̓t�F�����̓��͖����B
�����炢�������邾��H
���ꁫ�ʔ�������H
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
�l������v���O��������͂��Čv�Z���������������ȁB
"
�`�`�e�̂U�l�����s�ɏo�������B�h�����ł́A�R�l�����ƂS�l�����ɕ�����Ĕ�
�܂邱�ƂɂȂ����B���̂Ƃ��A�`�Ƃa�̂Q�l���K�����������ɔ��܂镔�������
���ʂ肠�邩�B
"
pm=gtools::permutations(2,6,0:1,re=T)
f <- function(x){
if(sum(x)>4|sum(x==0)>3) return(FALSE)
else if(x[1]==x[2]) return(TRUE)
return(FALSE)
}
sum(apply(pm,1,f))
> sum(apply(pm,1,f))
[1] 15
>
>>225
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
���q�吶�Ƀt�F�����Ă�������o���Ȃ���A�������ɓ�����̂ł��������B
���i�Ɗ�t���͕s�����f����h��ӈ��ɓ����O�Ɋ�t���������̐e����t�������Ƃ��ĕs���i�ɂȂ�̂łȂ����ƐS�z���ė������ƒk�������B
���i�Ɗ�t���͕s���Ƃ�����w�̕��j�͏�ɐ��������A�������͏�ɉR�����B
�k���ł́A
�u���q�l���ʐڂŐ������咣������Ί�t���ԋp���������i�ɂȂ�A�Ԉ�����咣�ł���Ί�t���v���ŕs���i�ɂȂ�v
�ƌ���ꂽ�B
�������w�������h��ӃV���c���͖ʐڂłȂ�Ǝ咣����悢���H �������Ƃ��P�����Ă�낤�@X�r�f�I�@�Ō������Ă݂�@���O�̗~����������ς����邼�Iw
�P�~�ʂR���A�T�~�ʂP���A�P�O�~�ʂQ���A�P�O�O�~�ʂQ���̍��v�Q�Q�W�~������
�Ă���B���܁A����������Ȃ��ł��傤�ǂ҂�����x�����̂ł�����z�͉�
�ʂ肠�邩�B�@�O�~�̓J�E���g���Ȃ��B
��s�v���O�����œ����ł�B
> nrow((expand.grid(0:3,c(0,5),c(0,10,20),c(0,100,200))))-1
[1] 71
�����������������Ă���Ɣn���ɂȂ�ȁB
���ꂷ��ł��Ȃ��n�����h��ӃV���c��B
���q�吶����t�F���������o���Ȃ�������
>>228
�Ԃ̑��l�ł��邱�Ƃ��킩���h�A�z���I�}�G����B
�t�F�����͂Ƃ����̂��H >>228
���|�I�ȓ��]�̍��I
�V���c��̓��]�͍������݁B
�����ĉR�����Ȃ����q�吶����u���Ȃ��̂������Ƃ��Ԉ���Ă��Ȃ���Ύ�R�L���A�t�F�������Ă�����v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H �Ȃ��@�I�i�j�[�l�^�ɂ��傤�ǂ�������@���܂��ɂ�w
A����F�̂U�l���A�����ɂȂ��Ďʐ^�B�e������B���ǂ���A��B�͕K���ׂ蓯�m
�ł���A�s����A��C�͕K���ׂ荇��Ȃ��悤�ɂ���悤�ȕ��ו��͉��ʂ肩�B
�R�s�ŏI���
pm=gtools::permutations(6,6)
f <- function(x)abs(which(x==1)-which(x==2))==1 & abs(which(x==1)-which(x==3))!=101
nrow(pm[apply(pm,1,f),])
���s����
> nrow(pm[apply(pm,1,f),])
[1] 192
>>233
����A���q�吶�t�@���̕����������B �悩�����ˁI����l�^�P������w
���䌧�z�O�s�Z�����@�I�i�j�[�D���̂��Ȃ��ց@�C�����悩�����ł����H
����E��́A�`�`�e�̂U�l�̐E���ō\������A���̂����d����тe�͐V�l�E����
����B�V�l�E���́A1�l�����܂��͂Q�l�����ł͊O�o�܂��͗���Ԃ����Ȃ��Ƃ�
��Ƃ��A�O�o����E���̑g�����́A���ʂ肠�邩�B
pm=gtools::permutations(2,6,0:1,re=T)
f <- function(x){
any(c(
(sum(x==1)==1 & (x[1]==1|x[2]==1)) | (sum(x==1)==2 & x[1]==1 & x[2]==1),
(sum(x==0)==1 & (x[1]==0|x[2]==0)) | (sum(x==0)==2 & x[1]==0 & x[2]==0)
))
}
pm[apply(pm,1,f),]
nrow(pm)- nrow(pm[apply(pm,1,f),]) - 1
���s����
> nrow(pm)- nrow(pm[apply(pm,1,f),]) - 1
[1] 57
> stairway(13,3)
[1] 1705
�����A�h��ӁB
�����o���ăJ�E���g���Ă���B
�I�}�G�̒�ӓ��]�ł̓t�F�����̓��͖����B
�����炢�������邾��H
���ꁫ�ʔ�������H
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
���q�吶�Ƀt�F�����Ă�������o���Ȃ���A�������ɓ�����̂ł��������B
���i�Ɗ�t���͕s�����f����h��ӈ��ɓ����O�Ɋ�t���������̐e����t�������Ƃ��ĕs���i�ɂȂ�̂łȂ����ƐS�z���ė������ƒk�������B
���i�Ɗ�t���͕s���Ƃ�����w�̕��j�͏�ɐ��������A�������͏�ɉR�����B
�k���ł́A
�u���q�l���ʐڂŐ������咣������Ί�t���ԋp���������i�ɂȂ�A�Ԉ�����咣�ł���Ί�t���v���ŕs���i�ɂȂ�v
�ƌ���ꂽ�B
�������w�������h��ӃV���c���͖ʐڂłȂ�Ǝ咣����悢���H
�Z�A���A�~�̂����ꂩ�̃}�[�N���P�������ꂽ�J�[�h������܂��B�Z�R���A
���Q���A�~�Q���̑S�V���̃J�[�h���A�����}�[�N�̃J�[�h���ׂ荇��Ȃ��悤�ɉ�
���ɕ��ׂ܂��B
��ԍ��Ɂ�����ׂ����A�c��̂U���̕��ו��͉��ʂ肠�邩�B
���Ɩʓ|
v=rep(1:3,c(3,2,2))
pm=permutations(7,7,v,set=F)
pm=unique(pm)
f<-function(x){
if(x[1]!=1) return(FALSE)
else{
if(
1 %in% diff(which(x==1))| 1 %in% diff(which(x==2))
| 1 %in% diff(which(x==3))
) return(FALSE)
}
return(TRUE)
}
nrow(pm[apply(pm,1,f),])
���s����
> nrow(pm[apply(pm,1,f),])
[1] 20
>>241
�����킩���n���Ȃ́H
�����ĉR�����Ȃ����q�吶����u���Ȃ��̂������Ƃ��Ԉ���Ă��Ȃ���Ύ�R�L���A�t�F�������Ă�����v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H �������������@�C�����悩�������[�@�����P����w
����ɂ��Ă��ނ�̏����W�\�͂͏G�킾�@���܂��͂���̂��l�X��{�点����
���[��Ȃ�����w
���䌧�z�O�s�Z�����@���܂��͒ʂ��Ă����a�@�Ŗ��N��������w
>>246
�����ɑ��l�肵�Ă���ǃA�z���I�}�G����B
�܂��ɍ������݂̓��]���ȁB
�����܂ŃA�z������A���c�����}����H ����ɂ����������Ȃ��́H
�n���Ȃ�B
�����ĉR�����Ȃ����q�吶����u���Ȃ��̂������Ƃ��Ԉ���Ă��Ȃ���Ύ�R�L���A�t�F�������Ă�����v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
A�`G�̂V�l���A�R�l�A�Q�l�A�Q�l�̂R�O���[�v�ɕ����镪�����͉��ʂ肠�邩�B
�ԁA�A���̂R�F�̃J�[�h���T�����A�v�P�T������܂��B�e�F�Ƃ��ɁA�P�`�T
�܂ł̐����P��������Ă��܂��B���̂P�T���̒�����R����I�т܂��B�I��
���R���ɏ����ꂽ���̘a���P�Q�ɂȂ�悤�ȑI�ѕ��͉��ʂ肠��܂����B
v=rep(1:5,3)
cmb=gtools::combinations(15,3)
head(cmb)
mat=matrix(v[cmb],nrow=3,byrow=T)
dat=t(mat)
head(dat)
f=function(x) sum(x)==12
nrow(dat[apply(dat,1,f),])
> nrow(dat[apply(dat,1,f),])
[1] 37
>
���䌧�z�O�s�Z�����@���܂��̂��Ƃ͑S���o���o���Ȃ�w
���������ǂ�����܂߂đ����̈�҂�G�������������ˁ@�P�P�P
����ɂ����������Ȃ��́H
�n���Ȃ�B
�����ĉR�����Ȃ����q�吶����u���Ȃ��̂������Ƃ��Ԉ���Ă��Ȃ���Ύ�R�L���A�t�F�������Ă�����v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
>>246
�����ɑ��l�肵�Ă���ǃA�z���I�}�G����B
�܂��ɍ������݂̓��]���ȁB
�����܂ŃA�z������A���c�����}����H
������݂������ȁB ���≴�͒����w��w���Ō�w�ȏo�g�̊Ō�t��w
�`���̕��䌧�z�O�s�Z�����@�P�P�P
���̒m�荇���ɕ�������@���[�A�C�c���@���̃N���N���p�[���ȁ@�����Ă��@�l�C������ˁ@�����܂�����@�P�P�P
�����ȕa�@�ɂ������ā@�����Ԃ�ƈ�҂�Ō�t�����点�Ă���ȁ@�����ƍr�炵�Ă�����w
>>258
��̑��l�𒆏����Ă���I�}�G���A�z�B
�I�}�G�̒m�荇�������痠�����w�e�^�҂���B f <- function(a) {
x=a-floor(a)
floor(a)+ifelse(x<0.5,floor(x),ceiling(x))
}
sim <- function(n=3,L=0,U=10){
x=runif(n,L,U)
y= numeric(n)
for(i in 1:n) y[i]=f(x[i])
f(sum(x)) != sum(y)
}
mean(replicate(1e3,sim()))
sim2 <- function(n){
pn=mean(replicate(1e3,sim(n)))
sqrt(n)*pn
}
sim3 <- function(n,L=0,U=100){
pn=mean(replicate(1e4,sim(n)))
pn
}
Sim3=Vectorize(sim3)
Sim3(3:10)
f <- function(a) {
x=a-floor(a)
floor(a)+ifelse(x<0.5,floor(x),ceiling(x))
}
sim <- function(n=3,k=1e4){
sub <- function(n){
x=runif(n)
y= numeric(n)
for(i in 1:n) y[i]=f(x[i])
f(sum(x)) != sum(y)
}
mean(replicate(k,sub(n)))
}
sim()
�C�ӂ�3�̎������l�̌ܓ����Đ����ɂ�����Řa�����̂ƁA
�a������Ă���l�̌ܓ����Đ����ɂ���ꍇ�Ő��l���قȂ�m�������߂�B
�������A3�̎����̏�������[0,1)��ԂœƗ��Ȉ�l���z�Ƃ���B
(�A�N�`���A���[���i������� - �ꕔ����)
�l�̌ܓ��Ŏv���o�����B
IEEE �ł͔C�ӂ̌��ʒu�ɂ�����ۂߏ����@�����̂悤�ɒ�߂Ă���i RjpWiki �̋L���C�w�H�w�̂��߂̃f�[�^�T�C�G���X����x �Ԑ� �� �� �� (�����H�w��) ������p�����j�D
��ԋ߂��ۂߌ��ʌ�₪1�����Ȃ�C���̐��Ɋۂ߂�D
��ԋ߂��ۂߌ��ʌ�₪2����ꍇ�́C�����������̂��̂Ɋۂ߂�i�ܓ�����łȂ��̂����蓾��I�j�D
�ۂߏ�����1�i�K�ōs�Ȃ�Ȃ���Ȃ�Ȃ��D
2.5�̊ۂ߂�2
3.5�̊ۂ߂�4
������Ċۂߌ덷���������Ȃ�Ɛ�������Ă����B
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x<=0.5)
}
f45(0.5)
round(0.5)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e3
while(tf==FALSE & k>0){
tf=sim(10)
k=k-1
}
tf
mean(replicate(k,sim()))
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x>=0)
}
f45(0.5) ; f45(1.5) ; f45(1.4999)
round(0.5) ; round(1.5) ; round(1.499)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e3
while(tf==FALSE & k>0){
tf=sim(10)
k=k-1
}
tf
mean(replicate(k,sim()))
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x>=0.5)
}
f45(0.5) ; f45(1.5) ; f45(1.4999)
round(0.5) ; round(1.5) ; round(1.499)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e3
while(tf==FALSE & k>0){
tf=sim(10)
k=k-1
}
tf
mean(replicate(k,sim()))
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x>=0.5)
}
f45(0.5) ; f45(1.5) ; f45(1.4999)
round(0.5) ; round(1.5) ; round(1.499)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e3
while(tf==FALSE & k>0){
tf=sim(10, print=F)
k=k-1
}
tf
mean(replicate(k,sim(print=F)))
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x>=0.5)
}
f45(0.5) ; f45(1.5) ; f45(1.4999)
round(0.5) ; round(1.5) ; round(1.499)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e3
while(tf==FALSE & k>0){
tf=sim(10, print=F)
k=k-1
}
tf
mean(replicate(k,sim(10, print=F)))
rm(list=ls())
f45 <- function(a) {
x=a-floor(a)
floor(a)+ (x>=0.5)
}
f45(0.5) ; f45(1.5)
round(0.5) ; round(1.5)
sim <- function(n=100,print=T){
x=runif(n,0,10)
M=mean(x)
tf <- abs(M-mean(round(x))) < abs(M-mean(f45(x)))
if(tf & print) cat(x,'\n')
return(tf)
}
tf=FALSE
k=1e5
while(tf==FALSE & k>0){
tf=sim(100, print=F)
k=k-1
}
k=1e5
mean(replicate(k,sim()))
>>264
rm(list=ls())
f45 <- function(a) { # �l�̌ܓ�
x=a-floor(a)�@# floor(a):a���Ȃ������K�E�X�L��[x]�Ɠ���,x:����������x�ɓ����
floor(a)+ (x>=0.5) # x��0.5�ȏ�Ȃ�P�������łȂ��Ȃ�O��������
}
f45(0.49) ; f45(1.5)
sim <- function(n=3,k=1e4){
sub <- function(n){
x=runif(n) # ��l���z����(����)���̔z��
y=numeric(n) # y�F�l�̌ܓ��ł̐���������z��
for(i in 1:n) y[i]=f45(x[i]) # ���̊e�������l�̌ܓ�����y�ɓ����
f45(sum(x))!=sum(y) # x�̑��a�̎l�̌ܓ�����y�̑��a���قȂ��TRUE��Ԃ�
}
mean(replicate(k,sub(n))) # k�̃V�~�����[�V�����ł�TRUE�̕p�x��Ԃ�
}
#
n=3:100
pn=sapply(n,function(n) sim(n,1e5))
plot(n,pn,bty='l',pch=19) �l�̌ܓ�
C++�@Java JavaScript Python2 PHP
IEEE
C# R Python3 Numpy
# �l�̌ܓ� vs IEEE
comp <- function(n=10,print=T){
x=sample((1:9)/10,n,rep=T) # 0.1,0.2,..,0.9����d����������n�I��
M=mean(x)
dif = abs(M-mean(round(x))) - abs(M-mean(f45(x))) # round��̕��ςƎl�̌ܓ���̕��ς̍�
if(dif!=0 & print) cat(dif<0,' : ',x,'\n') # ��������Ε\�� round�オ���������TRUE
return(dif)
}
>>265
���ۂɎ��s���Ċm�F���Ă݂�B
# �l�̌ܓ� vs �h�d�d�d with FUN(=mean) for x(=c(-0.9,-0.8,...,0.8,0.9))
comp <- function(n=10,FUN=mean,x=sample((-9:9)/10,n,rep=T),print=T){
X=FUN(x)
dif = abs(X-FUN(round(x))) - abs(X-FUN(f45(x))) # round��̎��s�Ǝl�̌ܓ���̎��s�̍�
if(dif!=0 & print) cat(dif<0,' : ',sort(x),'\n') # ��������Ε\�� round�オ���������TRUE
return(dif) # ����Ԃ� dif<0:round�D�� dif>0:�l�̌ܓ��D��
}
comp()
k=1e4
# mean
re=replicate(k,comp(print=F))
c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0))
# prod
re=replicate(k,comp(FUN=prod,print=F))
c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0))
# squared sum
comp(FUN=function(x) sum(x^2))
re=replicate(k,comp(FUN=function(x)sqrt(sum(x^2)),print=F))
c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0)) > k=1e5
> # mean
> re=replicate(k,comp(print=F))
> c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0))
�h�d�d�d �l�̌ܓ� ��������
0.25238 0.15829 0.58933
> # prod
> re=replicate(k,comp(FUN=prod,print=F))
> c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0))
�h�d�d�d �l�̌ܓ� ��������
0.00041 0.00000 0.99959
> # squared sum
> comp(FUN=function(x) sum(x^2))
[1] 0
> re=replicate(k,comp(FUN=function(x)sqrt(sum(x^2)),print=F))
> c(�h�d�d�d=mean(re<0),�l�̌ܓ�=mean(re>0),��������=mean(re==0))
�h�d�d�d �l�̌ܓ� ��������
0.40377 0.01346 0.58277
���ς��炢�ł͑卷�͂Ȃ����A���v�̓����v�Z�ł��������a�Ɋւ��Ắ@IEEE�̊ۂ߂̕������|�I�Ɍ덷�����Ȃ��Ȃ��B
���������ޒ�ӃV���c�����炢�̍����݂ĂƂ��B
>>264
rm(list=ls())
pn <- function(n=3,k=1e3){ # 1-pn = -1/2 < ��(1��n)xi < 1/2, where xi~U(-1/2,1/2)
f <- function(n) abs(sum(replicate(n,runif(1,-1/2,1/2)))) < 1/2
1-mean(replicate(k,f(n)))}
pn(3,1e5)
y=sapply(1:100,pn)
plot(n,y) >>260
���܂������A�m�b�x��̏�Q�҂���Ȃ��́H "
�C�ӂ�3�̎������l�̌ܓ����Đ����ɂ�����Řa�����̂ƁA
�a������Ă���l�̌ܓ����Đ����ɂ���ꍇ�Ő��l���قȂ�m��1-pn�����߂�B
�������A3�̎����̏�������[0,1)��ԂœƗ��Ȉ�l���z�Ƃ���B
"
fpn <- function(n=3,k=1e3){ # 1-pn = -1/2 < ��(1��n)xi < 1/2, where xi~U[-1/2,1/2)
f <- function(n) abs(sum(replicate(n,runif(1,-1/2,1/2)))) < 1/2
mean(replicate(k,f(n)))
}
y=sapply(1:10,fpn)
plot(1:10,y,pch=19,bty='l')
fpn <- function(n=3,k=1e3){ # 1-pn = -1/2 < ��(1��n)xi < 1/2, where xi~Unif[-1/2,1/2)
f <- function(n){ # 1 -pn = (n-1)/2 < ��(1��n)Xi, where Xi~Unif[0,1)
s=sum(replicate(n,runif(1)))
(n-1)/2<s & s<(n+1)/2 # is round after sum(RAS) == sum after round(SAR)?
}
mean(replicate(k,f(n))) # proportion of RAS == SAR
}
n=3
pn=replicate(1e4,fpn(n,k=1e3))
hist(pn,freq=F,col='lightblue')
mean(pn) ; sd(pn)
s=replicate(1e5,sum(replicate(n,runif(1))))
mean(s)
sd(s)
m=n/2
sd=sqrt(n/12)
curve(dnorm(x,m,n),0,n,bty='l')
1- (pnorm((n+1)/2,m,sd)-pnorm((n-1)/2,m,sd))
# Qn=1-Pn Xi~Unif[-1/2,1/2)�@Pr[��(1:n)Xi��[-1/2,1/2)
"
���I=[-1/2,1/2)�ň�l���z����Ɨ���n�̎����𑫂��Ă�I�Ɋ܂܂��m����P[n]�Ƃ����
P[n]=(1/��)��[-��,��](sinx/x)^(n+1)dx
�ł���B
"
Pn <- function(n){
if(n==0) return(1)
if(n==1) return(1)
f<-function(x) (sin(x)/x)^(n+1)/pi
integrate(f,-Inf,Inf)$value
}
sapply(0:10,Pn)
#
f <- function(x,n=3) (sin(x)/x)^(n+1)/pi
integrate(f,-Inf,Inf)
vf=Vectorize(f)
curve(vf,-pi,pi,bty='l')
"A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����N���m���ɐ����҂ƒf��ł��邩�H
A�u�R���̕��������҂�葽���v
B�uH�͉R���ł���v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F�������҂ł���v
"
TE=expand.grid(0:1,0:1,0:1,0:1,0:1,0:1,0:1,0:1)
colnames(TE)=LETTERS[1:8]
tail(TE)
TE=expand.grid(0:1,0:1,0:1,0:1,0:1,0:1,0:1,0:1)
colnames(TE)=LETTERS[1:8]
f <- function(x){
all(c(
x[1]==1 & sum(x==0)>sum(x==1) | x[1]!=1 & !(sum(x==0)>sum(x==1)),
x[2]==1 & x[8]==0 | x[2]!=1 & x[8]!=0,
x[3]==1 & x[2]==0 | x[3]!=1 & x[2]!=0 ,
x[4]==1 & (x[3]==0 & x[6]==0) |�@ x[4]!=1 & !(x[3]==0 & x[6]==0),
x[5]==1 & sum(x==0)>=1�@| x[5]!=1 & !(sum(x==0)>=1),
x[6]==1 & sum(x==0)>=2�@| x[6]==0,
x[7]==1 & x[5]==0 | x[7]==0,
x[8]==1 & (x[1]==1 & x[6]==1) | x[8]==0
))
}
TE[apply(TE,1,f),]
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�C���o�E���h�Ƃ���߂�ׂ��B���X�N�������ă��^�[���������B�����l��SARS���N�����āA�܂����ꂾ��B�쐫�����H���悤�ȘA�����ړ�����Ώ�ɂ����������X�N���N����
�����悤�ȏK������A���́A���E�ɂ͂�������B���܂ł͕n�R���ŗ��s�Ȃo���Ȃ����������B�A�t���J�Ƃ��������ʂɗ��s�҂�����悤�ɂȂ�A��a�̊����Ƃ��L�蓾��
��i���ʂ����s��������Ώ[���B���X�N���邩�疳���ɃC���o�E���h�Ȃ��K�v�Ȃ��B��́A���{�͕���������ŕ������߂Ƃ��ł��Ȃ����ȁB���܂ł̓��b�L�[����������
SARS�̎��͒����l�́A�܂��n�R�ŗ��s�Ȃ�Ėw��ǂ����Ȃ��������A�����̈ړ������Ȃ���������L����Ȃ������B���͈Ⴄ��B���ƁASARS�̎��́A��s�@���ł����肩�Ȃ����Ă���
����́A�����҂��ł��炩����SARS�ɑ���������������s���Ă���B�����A���Ȃ芴���҂��o�Ă�ƍl��������������
�܂�����Ȃ�
���₳�Ȃ�
�������߂�
���ꂪ�ł��Ȃ������Ƃ̓p���f�~�b�N�Ȃ����Ƃ��̎�Ƃł��B
23���@�������{�@�����s��
24���@���{�����A�t�ߒ����l�ό��q���}�j��
�H��
�t�߂ɍۂ��āA�����Ă܂��A�I�����s�b�N�E�p�������s�b�N���̋@���ʂ��āA�X�ɑ����̒����̊F�l���K������邱�Ƃ��y���݂ɂ��Ă��܂��B���̍ہA���Г����ȊO�̏ꏊ�ɂ������^�сA���̓y�n�Ȃ�ł͂̓��{�炵���������Ē�����K���ł��B
25���A26�����{�����͎��@�őҋ@
28���@�������{�A�����l�̊C�O�c�̗��s���֎~
�������߂�C0���������炻���g�U�~�܂��
�ڐ�̏t�߃C���o�E���h�ړ��Ăł����ƒ����̊ό��q���v��������
f <- function(n,prec=10000){ # �� 1/k�������\������
if(n==1){
cat(' ',1,'\n')
invisible(1)
}else{
GCD <- function(a,b){�@ # ���[�N���b�h�̌ݏ��@
r = a%%b # a=bq+r �� a%%b=b%%r�ōő���\��
while(r!=0){a = b ; b = r ; r = a%%b}
b }
library(Rmpfr)
one = mpfr(1, prec) # 1(one)��10000�����x�ɐݒ�
nn = 1:n # nn : 1 2 3 ... n
nume=numeric(n) # ���q�̗e��
for(i in nn) nume[i] = prod(nn[-i])*one # nn����i�Ԗڂ̗v�f�������ď�Z�����x�A�b�v
nume = mpfr2array(nume, dim = length(nume)) # mpfr2array�ʼn��Z���\�ɂ���
Nume = sum(nume)�@# nume�̑��a���v�Z���ĕ��q��
Deno=factorialZ(n) # ���� n! = factorial(n*one)
gcd = GCD(Nume,Deno) # Numerator/Denominator���邽�ߍő�����v�Z
res=list(nume = Nume/gcd,deno=Deno/gcd,ratio=as.numeric(Nume/Deno)) # �ő���ŏ��Z����
�@# �����\�� give.head=FALSE��header����,digits.d�Ō������w��
# capture.output�ŕϐ��Ɏ�荞��
nm = capture.output(str(res$nume, give.head=FALSE,digits.d = prec))
dn = capture.output(str(res$deno, give.head=FALSE,digits.d = prec))
cat(paste0(nm,'/',dn,'\n'))
invisible(res)
}}
for(i in 1:50) f(i)
f(77)
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
>>287
���@���|�@�����������������i���C�����������P�O�O�O�O�j�o�@���@���@�P�^���������\������
�@�@�����i�������P�j�o
�@�@�@�@�������i�V�@�V�C�P�C�V\���V�j
�@�@�@�@�������������������i�P�j
�@�@�p���������o
�@�@�@�f�b�c�@���|�@�����������������i���C���j�o�@�@���@���[�N���b�h�̌ݏ��@�@
�@�@�@�@���@���@���������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@���������{���@�ˁ@�������������������ōő���\��
�@�@�@�@�����������i���I���O�j�o���@���@���@�G�@���@���@���@�G�@���@���@���������p
�@�@�@�@���@�p
�@�@���������������i�q���������j
�@�@�������@���@���������i�P�C�@���������j�@���@�P�i�������j���P�O�O�O�O�����x�ɐݒ�
�@�@�����@���@�P�F���@�@�@�@�@�@�@�@�@�@�@�@���@�����@�F�@�P�@�Q�@�R�@�D�D�D�@��
�@�@�������������������������i���j�@�@�@�@�@���@���q�̗e��
�@�@�������i���@�����@�����j�@���������m���n�@���@���������i�����m�|���n�j���������@���@�������炉�Ԗڂ̗v�f�������ď�Z
�@�@���������@���@���������Q�����������i���������C�@�������@���@�������������i���������j�j�@���@���������Q�����������ʼn��Z���\��
�@�@�m�������@���@�������i���������j�@���@���������̑��a���v�Z���ĕ��q��
�@�@�c���������������������������y�i���j�@���@����@���I�@���@�������������������i�����������j
�@�@�������@���@�f�b�c�i�m�������C�c�������j�@���@�ő�����v�Z
�@�@�����������������i���������@���@�m�������^�������C�����������c�������^�������C�����������������D���������������i�m�������^�c�������j�j�@���@�ő���ŏ��Z����
�@�@���@���������������D�������������Ő��肓�����������Łm�P�n������
�@�@�����@���������������i���������������D�������������i�����������������j�m�Q�n�C�T�C�����������i�����������������j�j�@���@�W�m�P�n�@�P�Q�R�S�D�D�W�@������̂T�����ڂ���Ō�܂�
�@�@�����@���������������i���������������D�������������i�����������������j�m�Q�n�C�T�C�����������i�����������������j�j
�@�@�������i�����������O�i�����C�V�^�V�C�����C�V\���V�j�j
�@�@�������������������i�������j
�p�p #Reed-Frost Model
ReedFrost=function(
p=0.04,
N=100,
T=40)
{
q=1-p
I=numeric(T)
S=numeric(T)
I[1]=1
S[1]=N-I[1]
for(t in 1:(T-1)){
I[t+1]=S[t]*(1-q^I[t])
S[t+1]=S[t]-I[t+1]
}
plot(1:T,I,type="l",lwd=2, ylim=c(0,N),xlab="time",ylab="persons",main=paste("Reed-Frost Model p= ",p))
lines(S,lty=2,col=2,lwd=2)
lines(N-S,lty=3,col=3,lwd=2)
legend("topright",bty="n",legend=c("Infected","Susceptible","Immunized"),lty=1:3,col=1:3,lwd=2)
}
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�����{�u����܂Ŏ��{���Ă������ۍ��Ȃǂ̃t�F�[�Y��������i�����グ��K�v������
���{�ς�O�@�t�ߏj������
�t�߂ɍۂ��āA�����Ă܂��A�I�����s�b�N�E�p�������s�b�N���̋@���ʂ��āA�X�ɑ����̒����̊F�l���K������邱�Ƃ��y���݂ɂ��Ă��܂��B
���Ƃ�ł��������������ĂH�Q���O�\��Y��
https://www.cn.emb-japan.go.jp/itpr_ja/00_000351.html
����not found�ɂȂ��Ĉ��{���y�[�W�������ď؋��B�ł��������� �܂��x����Ă���l�������������ǁA
�C���o�E���h�A�C���o�E���h�Ƒ�����Ă��邯�ǁA
�C���o�E���h�̏���z�Ȃ�Ăf�c�o�̂P���ɂ������Ȃ��A
�ƌv�̑�����z�ɑ��Ă��A��������1.5%�B
������u�ό������v���́A
�����������{���C���o�E���h�Ɏx�����Ă��邩�̂��Ƃ��������x���āA
�����ꕔ�̐l�B�̋��ׂ��̂��߂�
��ʂ̒����l�ό��q����������Ċό����Q���T���U�炵�Ă����������A
���܂�吨�̂���{�l�̐�������������Ă���B
�A�X�y�Ől�Ƃ̃R�~���j�P�[�V��������ꂸ�A���w�����ӂł������B
�^��ʍ�����w�𑲋Ƃ���B
��Ǔ��ǂ���B�㋉��Ƃ̃R�~���j�P�[�V��������ꂸ�A(�����C�㎞��A�k�퐧��)��ǎ���͖��҈�������A�n���̕a�@�ɔ�����B�n���̕a�@�ł����ƓƊw�ŗՏ��ɗ�ށB���A�܂Ƃ��ɋ��炳�ꂸ�Ɗw�̂��߂Ɍn���������Տ��ɂ��Ắc�B
��ǂ����̊Ԃɂ����߂āA�×{�^�a�@�ɋΖ�����B
�����̈�t���w��̗v�E�A��a�@�̗v�E�ɏA���Ă��鎖���l�b�g�Ō��ċ��܂��������~�ς�����B
�E��Ɏ������̐���������Ă����i������B
���������w�������̕ȂɁI���ᛂ��N�����B
2ch(��5ch)�ŋ������悤�ɟT���𐰂炷�B
���{�́u�Ή����x���v�Ƃ��ł͂Ȃ�
���V�^�x���嗬�s�ɂȂ��Ă�Ƃ���
�ǂ�ǂ�ό��q���ĉ������I
�����{�Ől����l�������N���Ă�Ƃ���
�ό��q����ƌo�ςւ̉e�����o�邩��I
��
���҂��ǂ�ǂ�Ăэ���
180���̂�����60�l���ꖇ�Â����Č���Ȃ��U�l�ɋ߂��l���ɓ����肪�o��悤�ɂ���ɂ�180���̂����ɉ��������������悢�ł��傤���H
library(gmp)
n=180 ; r=60
chooseZ(180,60)
E <- function(x,n=180,r=60){
y=chooseZ(n,r)
z=0
for(i in 0:x) z = z + i*chooseZ(x,i)*chooseZ(n-x,r-i)
RE=z/y
cat(x,':',as.numeric(RE),'\n')
invisible(RE)
}
> for(i in 6:20) E(i)
6 : 2
7 : 2.333333
8 : 2.666667
9 : 3
10 : 3.333333
11 : 3.666667
12 : 4
13 : 4.333333
14 : 4.666667
15 : 5
16 : 5.333333
17 : 5.666667
18 : 6
19 : 6.333333
20 : 6.666667
>>301
�V�~�����[�V�������Ċm�F�B
sim <- function(x,n=180,r=60,k=1e4){
g <- function(x){
y=rep(1:0,c(x,n-x))
sum(sample(y,r))
}
mean(replicate(k,g(x)))
}
Sim=Vectorize(sim)
cbind(10:20,Sim(10:20))
> cbind(6:20,Sim(6:20))
[,1] [,2]
[1,] 6 2.0074
[2,] 7 2.3418
[3,] 8 2.6643
[4,] 9 3.0059
[5,] 10 3.3244
[6,] 11 3.6494
[7,] 12 3.9859
[8,] 13 4.3330
[9,] 14 4.6727
[10,] 15 5.0071
[11,] 16 5.3384
[12,] 17 5.6876
[13,] 18 5.9835
[14,] 19 6.3356
[15,] 20 6.7060
�P�W���ߎ����Ă���B �����܂ł���1�T�Ԃ��ȁ`���̌������F��I
4������͂��悢���t�Ƃ��ẴX�^�[�g���ˁI�ꏏ�Ɋ撣�낤�I
H(n) = ��[k=1,2,...,n] 1/k
�Ƃ���BH(n)�������ŕ\�����Ƃ��̕��q�̐�����f(n)�ƕ\���B�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
f(1000)�����߂�B
5336291328229478504559104562404298040965247228038426009710134924845626888949710175750609790198503569140908873155046809837844
2172117885009464302344326566022502100278425632852081405544941210442510142672770294774712708917963967779610453224692426866468
8882815820719848971051107968732493191555293970175089315645199760857344730141832840117244122806490743077037366831700558002936
59235088589360235285852808160759574737836655413175508131522517
/
7128865274665093053166384155714272920668358861885893040452001991154324087581111499476444151913871586911717817019575256512980
2640676210092514658710043051310726862681432001966099748627459371883437050154344525237397452989631456749821282369562328237940
1106880926231770886197954079124775455804932647573782992335275179673524804246363805113703433121478174685087845348567802188807
5373249921995672056932029099390891687487672697950931603520000
�����h��ӁA���w�Z�łĂ�����������炢�m���Ă��邾�낤�B�v�Z�������Ă��邩�m���߂Ă����Ă���B
�o�O�t���v���O�����ł̌��ʂ𐔊w�ɓ��e���ēP������A�f�o�b�O���ċN�����������B
�����͑�w�Ŋw���̏W�听����ˁB������ƕ����Ă����l�͕K�����i����I
�O�Ȍn���Ƃ����Ƃ������Ȃ��A����͎R�قǂ���A
�O�̑O�̓V�c�̌��ǎ�p���ꂽ�搶�͉�����������
���̎��������z�����炱�ꂩ��̐l���̎��M�ɂȂ邾�낤�@��t�̐����͂����ւ���ǂ��[���������̂ɂȂ�I�撣������撣�������߂��Ă���
�y�ߕ�z��������̋A����192�l�A���{���p�ӂ����z�e����140�������Ȃ��A2�l1�g�̑������ɂȂ邱�Ƃɓ{��
library(gmp)
allocate.rooms <- function(m,n){ # m:rooms n:people
if(m==n) return(factorialZ(m))
else if(m==1) return(1)
else m*Recall(m,n-1) + m*Recall(m-1,n-1)
}
allocate.rooms(140,192)
>>308
�V���c���ɂ����̊�p�Ȑl�͂��邪�A������p�Ȃ�V���c���Ȃɂ͍s���Ȃ��B
�܂��A���Q�Ə���͗������w�̉\�������Ȃ��炵���B �������̎����͗������w�����ݐi�s�`�ł��邱�Ɣ@���ɂ��߂�����������ˁB
�V���c��̎g���͗������w�o�ō����^���̐擪�ɗ����Ƃ���B
�������w�̊w�������Џ����ɂ��Ȃ�������A�M���̉͂Ȃ��ˁB�܂�A���܂Ōo���Ă��V���c��呲�������o�J�Ɖ����͐@���Ȃ��B�V���c�o�g�҂����A�������w�Ɍ��������������i����ׂ��B
�������w��t�̖Ƌ����D���I�̍����^���̐擪�ɗ��Ă悢���B
�l���������w�Ƃ��A�����Ă���M���̉͂Ȃ��B
���̕s��p�ȃV���c�オ���̂������̂��N�������낤�ȂƎv���Ă�����

������\�ɂł�������������ƂЂǂ��͉̂B������Ă���Ɖ��͎v���Ă���B �����������e���݂�Ƃł���ƕ������Ă��Ă��������ɂ���ƋC������邢�B
"
P,Q,R��ϗ�(��)����Ƃ���Ƃ��A����2�̗ϗ�(��)���͓��l�ł��邩�A���l�łȂ����B
�^�U�\���쐬���A���肹��
��R��(Q�@�Ɂ@P) �� R�@�Ɂ�(Q�@�Ɂ@P)
"
f <- function(p,q,r){
naraba<-function(x,y) !(x&!y)
naraba(!r,q|p)
}
g <- function(p,q,r) r | !(q|p)
sg = expand.grid(c(TRUE,FALSE),c(TRUE,FALSE),c(TRUE,FALSE))
colnames(sg)=c('P','Q','R')
d1=mapply(f,sg[,1],sg[,2],sg[,3])
d2=mapply(g,sg[,1],sg[,2],sg[,3])
cbind(sg,d1,d2)
P Q R d1 d2
1 TRUE TRUE TRUE TRUE TRUE
2 FALSE TRUE TRUE TRUE TRUE
3 TRUE FALSE TRUE TRUE TRUE
4 FALSE FALSE TRUE TRUE TRUE
5 TRUE TRUE FALSE TRUE FALSE
6 FALSE TRUE FALSE TRUE FALSE
7 TRUE FALSE FALSE TRUE FALSE
8 FALSE FALSE FALSE FALSE TRUE
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
315 ���O�F���ځ`��[NGWord:���كV���c���كV���c] ���e���F���ځ`��
�RD���E�̖��
��ӂ̒�����10m�̗����̂̃v�[���̈�̊p�ɊĎ�����u��.���̊Ď����͐����͕b��1m��,�v�[ ���̉���͕b�� 2m �ňړ�������̂Ƃ���.���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b �K�v���v�Z����.
di<-function(X,Y) sqrt(sum((X-Y)^2)) # X,Y�̋���
Lx=Ly=Lz=10 # �v�[���̑傫��
vs=2 # �v�[���T�C�h�̈ړ����xvelocity along side
vw=1 # �������x velocity in water
O=c(0,0,0) # �Ď����̈ʒu
S=c(x,y,z) # Swimmer�̈ʒu
sim <- function(S){
# O-S (O���琅�v)
O=di(O,S)/vw
# O-X(X���ォ�琅�v)
f=function(x) x/vs+di(c(x,0,0),S)/vw
OX=optimise(f,c(0,Lx))$obj
# O-Y(Y���ォ�琅�v)
f=function(y) y/vs+di(c(0,y,0),S)/vw
OY=optimise(f,c(0,Ly))$obj
# O-Z(Z���ォ�琅�v)
f=function(z) z/vs+di(c(0,0,z),S)/vw
OZ=optimise(f,c(0,Lz))$obj
# O-X-Y(X��S�����s����Y���ォ�琅�v)
f=function(y) Lx/vs+y/vs+di(c(Lx,y,0),S)/vw
OXY=optimise(f,c(0,Ly))$obj
# O-Y-X(Y��S�����s����X���ォ�琅�v)
f=function(x) Ly/vs+x/vs+di(c(x,Ly,0),S)/vw
OYX=optimise(f,c(0,Lx))$obj
# O-Y-Z(Y��S�����s����Z���ォ�琅�v)
f=function(z) Ly/vs+z/vs+di(c(0,Ly,z),S)/vw
OYZ=optimise(f,c(0,Lz))$obj
# O-Z-Y(Z��S�����s����Y���ォ�琅�v)
f=function(y) Lz/vs+y/vs+di(c(0,y,Lz),S)/vw
OZY=optimise(f,c(0,Ly))$obj
# O-Z-X(Z��S�����s����X���ォ�琅�v)
f=function(x) Lz/vs+x/vs+di(c(x,0,Lz),S)/vw
OZX=optimise(f,c(0,Lx))$obj
# O-X-Z(X��S�����s����Z���ォ�琅�v)
f=function(z) Lx/vs+z/vs+di(c(Lx,0,z),S)/vw
OXZ=optimise(f,c(0,Lz))$obj
# O-X-Y-Z(X,Y��S�����s����Z���ォ�琅�v)
f=function(z) Lx/vs+Ly/vs+di(c(Lx,Ly,z),S)/vw
OXYZ=optimize(f,c(0,Lz))$obj
# O-X-Z-Y(X,Z��S�����s����Y���ォ�琅�v)
f=function(y) Lx/vs+Lz/vs+di(c(Lx,y,Lz),S)/vw
OXZY=optimize(f,c(0,Ly))$obj
# O-Y-Z-X(Y,Z��S�����s����x���ォ�琅�v)
f=function(x) Ly/vs+Lz/vs+di(c(x,Ly,Lz),S)/vw
OYZX=optimize(f,c(0,Lx))$obj
route=c('O','OX','OY','OZ',
'OXY','OYX','OYZ','OZY','OZX','OXZ',
'OXYZ','OXZY','OYZX')
t=c(O,OX,OY,OZ,OXY,OYX,OYZ,OZY,OZX,OXZ,OXYZ,OXZY,OYZX)
m=min(t)
cat(route[which(t==m)],':',m,'\n')
invisible(m)
}
options(digits=7)
(opt=optim(c(5,5,5),sim,method='L',control=list(fnscale=-1)))
opt[1]
opt[2]
> opt[1]
$par
[1] 7.691099 7.691099 7.691099
> opt[2]
$value
[1] 13.26518
�Ō�̃��X�g�X�p�[�g���ˁI�����̎c��Ȃ��悤�Ɋ撣���I
���܂ŕ����Ă������Ƃ͖��ʂł͂Ȃ����Ƃ𖡂���ė~�����I�܂Ƃ܂����������邱�Ƃ͂��̐悠�܂薳����I
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�����ɗ������l�̍��݂͕|���˂�
�l��▯���Ȃǖ{�l���I���ł��Ȃ����Ƃ������Ƃ����ʂ͍��ʂ̔ᔻ��Ƃ�Ȃ����A
�h��ӃV���c���i�w�͖{�l�̑I������Ȃ��B
����ȁI
�s���̖����e
>>
���͏��a�̎���ɑ�w�������ǁA�͍̂��������ʊ��������A���ꖯ�̂��߂̓���w�Z�Ƃ����C���[�W�ŊJ�ƈ�̃o�J���q�ȊO�͒N�����悤�Ƃ��炵�Ȃ������B
�펯�I�ɍl���āA���疜�Ƃ����@�O�ȋ����āA���������Ǝ҂�������҂�����o�J���̗������̂ƎU�X�l����̂��킩���čD���D��Ńh��ӈ�ɍs���������͈�l�����܂���ł����B
�{�l�ɂ͖ʂƌ������Ă͌���Ȃ�����ǁA�����炢�̔N��̐l�Ԃ́A�����炭�͂W�|�X���̓h��ӈ㑲�����ł��u���̂����Ȃ��Ɣ������Ă�A���̗����o�J���v�ƐS�̒�Ōy�̂��A�}���Ă����B
���̖{�l�ɂ͖ʂƌ������Ă͐�ɂ���Ȃ��Ƃ͌���Ȃ����ǂˁB
<<
�������̎����͗������w�����ݐi�s�`�ł��邱�Ɣ@���ɂ��߂�����������ˁB
�V���c��̎g���͗������w�o�ō����^���̐擪�ɗ����Ƃ���B
�������w�̊w�������Џ����ɂ��Ȃ�������A�M���̉͂Ȃ��ˁB�܂�A���܂Ōo���Ă��V���c��呲�������o�J�Ɖ����͐@���Ȃ��B�V���c�o�g�҂����A�������w�Ɍ��������������i����ׂ��B
�������w��t�̖Ƌ����D���I�̍����^���̐擪�ɗ��Ă悢���B
�l���������w�Ƃ��A�����Ă���M���̉͂Ȃ��B
>>319
����H��̓��������R�����Ɋg���������B
�����ʼn����Ȃ�Δ������K�v�ɂȂ�B
�����w�����ʼn�������l�\���ȁB >>329
�������������ł�����킵����B ����20���N�̖��E����[��@����f���ł͗L������[��
�w�K���Ȃ��A�z������͓��c�������Ǝv����ȁB
�悭������w�����ꂽ�ˁB�̂��ˁB���Q�����ǂˁB���Ƃ܂ł����E�������ˁ@w w w
�����ō�����w�i�w���e�Ƃ̈Öق̗����B
����͊���~�߂ɗ��T��I���B
>>323
�R���s���[�^�g���Ȃ�A���������̂�肱�����̕��������[���ȁB
���w�̌����Ȃ琔�l�������Έ�ӂɖʐςƂ��o�Ă��邯�ǁA�u�w���܂߂��Տ��͊m�����ۂ������Ă��邩��
���R������ł�B�@SEIR���f���ɏ]���V�~�����[�V�����v���O������g��ł݂��B
�T�C�R���̂P�̖ڂ̏o��m����1/6������Ƃ�����6������K���P���P��ł�킯�ł͂Ȃ��B
�P�l�̊����҂��܂ދA���҂Q�O�l�𑊕����ɂ��ꂽ�Ƃ��̃V�~�����[�V����������B
�L���肪��������ꍇ�ƑJ������ꍇ������̂��݂ĂƂ��B

���d���Z���ς��Ƃ��SEIR���f���̃O���t�Ɏ������Ă����̂��낤���A�����I�ɂ͉��x���J��Ԃ���킯�ł͂Ȃ��B ���A���͓��c�ł������ł��Ȃ������w��w���Ō�Ȃ̊Ō�t�Ł[��
�{���̒Ⴂ���ɑ��Q���Ă���ƍ��i�����l w
���̘A���͂悭���ׂ��������ȁ@�����ǂ�����
��ȑ�w�����ȏȂ̊NJ��ł��邱�Ƃ���m���A�z���h��ӃV���c���B
�P�P�P�@���Ȃ�̎d�����Ă�́H�o���o������[��
�t�F���ɂ͋������Ȃ��̂��H
����A�P�ɓ������������Ȃ낤�ȁB
���̃X���ɍ��킹�Ă݂��B
�����O�Ɋ�t�������h��ӃV���c���̐e��
��t�������Ƃ��ĕs���i�ɂȂ�̂łȂ����ƐS�z���ė������ƒk�������Ƃ���A���i�Ɗ�t���͕s���ł���A
���q�l���ʐڂŐ������咣�������
��t���ԋp��
�������i�ɂȂ�
�ƌ���ꂽ�B
�������͉R�����Ȃ��B
�������w�������h��ӃV���c���͖ʐڂłȂ�Ǝ咣����悢���H
�_���I�v�l���ł���́H
�n���Ȃ́H
�������w�Ȃ�B
�͂��E�ɂ��Ȃ����@���A�������@�����ƕa�@�ɒʉ@������I�Ȃ� w
�����Ȑ搶�������肳����Ȃ�@�˂� w ���A�����x������ w
�����̂łȂ��I�����s�b�N�T�C�Y�E�v�[���Ƃ��Đ��E�L�^�ŊĎ������ړ�����ꍇ���v�Z���Ă݂�B
"�I�����s�b�N�T�C�Y�E�v�[��50m�~25m�̐��̓������v�[���̈�̊p�ɊĎ�����u���B
�Œ�2.0 m (6 ft 7 in)�A3.0 m (9.8 ft)�����������
�Ƃ������ƂȂ̂ŁA���[2.5m�Ƃ���B
���̊Ď����͐��E�L�^�ňړ�������̂Ƃ���B
���j100m���R�` 46�b91�Ő������ړ�
����100m9�b58�Ńv�[���T�C�h���v�ړ�
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b�K�v���v�Z����B
�ǂ̂�������u��ӎ����v�Ƃ����́H
�ǗтƂ��H
> (Scrit=opt$maximum * e ) # O����Œx�_�܂ł̒����������P�ʃx�N�g�� =�@�Œx�n�_Scrit�̍��W
[1] 25.717152 12.858576 1.285858
> sim2(opt$max,print=T)
OYZX : 8.594513
�Ƃ������ʂɂȂ���
>>351
������呲�ő��Ƒ�w�������Ȃ��Ȃ��ӎ�����傾�낤�ˁB
���̃X���Ŕn�����N���Ă����͗������w�̎��o������낤�B �f���炵�������ł��I����Ȑl�������Ƃ�����܂���I�f���炵���I
���܂���莄����w���Ƃ��Ĉ�҂ɂȂ��Ă�搶�̕���������B�Ȃ� w�͂��� w
�E�l�}�V�[���V���c�̈�t�Ƌ���������ɂ���
������w���͑S�ĉ�̂���
�e�q�O������@65�̃n�Q
�{�錧�̈�t��̗�������Ă��炻���ɂ��Ă��
�o�J���ƃo�J���q���ǂ�������������Ɋ��荞�܂����̂�����
�Ǘт͒�ӂȂ̂��H
����Ƃ����}���Ƃ��H
���������̑O�ATV�����Ă����ǁA�ǂ����Y�ꂽ����
�֓��̂��܂蕷�������Ƃ��Ȃ��悤�Ȏ�����呲�̈�ҁA
�~�}�̖���Ƃ��Ŋ��Ă����ǁA������呲������
���X�͓��呲�̈�҂ő��ƌ�Ɏ������ɓ���Ȃ����Ă����B
�ƂĂ��o�J�ɂł����҂��肶��Ȃ��Ǝv�����ǁB
���͒n���������i��E��n��g�j������
����Ȃ��100�����i�ł��Ȃ���B
�X�ɁA��≻�B
"
4�������E�̖��
��ӂ̒�����10m�̗����̂̃v�[���̈�̊p�ɊĎ�����u��.
���̊Ď����͐����͕b��1m��,���@�̂̂U�ʏ�͕b�� 2m �ňړ�������̂Ƃ���.
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b �K�v���v�Z����.
"
>>358
���ꑲ�ŗ��O�ɍĎ��Ĉ�t�ɂȂ����^�^���������a�@�̊�Ȉ�t�������B
����Z����̈�Ȏ��ȓ��w�����ǁA�Q�`�R���͍Ďg�B�قƂ�Ǔ��呲�Ƌ��呲�������ȁB
�����͍��͊w�m���w�����������炾�낤��呲�͂��Ȃ������B >>359
Lx=10; Ly=10; Lz=10 # �v�[���̑傫��
L=c(Lx,Ly,Lz)
Ld=sqrt(sum(L^2)) # �Ίp���̒���
e=L/Ld # �����P�ʃx�N�g��
vs=2 # �Ǐ㑬�xvelocity along side
vw=1 # �������x velocity in water
O=c(0,0,0) # �Ď����̈ʒu
dit<-function(X,Y,v) sqrt(sum((X-Y)^2))/v # X,Y�̈ړ����v���� distance->time
sim <- function(ld,print=FALSE){ # ld:���_��S(�Ίp����)�̋���
S=ld*e # swimmer�̈ʒu
# OS ������
OS=dit(0,S,vw)
# X0 (����x=0�������)
f<-function(y,z) dit(c(0,y,z),0,vs)+dit(c(0,y,z),S,vw)
X0=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method='L')$value
# Y0 (����y=0�������)
f<-function(x,z) dit(c(x,0,z),0,vs)+dit(c(x,0,z),S,vw)
Y0=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method='L')$value
# Z0 (����z=0�������)
f<-function(x,y) dit(c(x,y,0),0,vs)+dit(c(x,y,0),S,vw)
Z0=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method='L')$value # X10 (����x=10�������)
f<-function(y,z) dit(c(Lx+y,z),0,vs)+dit(c(Lx,y,z),S,vw)
X10=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method='L')$value
# Y10 (����y=10�������)
f<-function(z,x) dit(c(Ly+x,z),0,vs)+dit(c(x,Ly,z),S,vw)
Y10=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method='L')$value
# Z10 (����z=10�������)
f<-function(x,y) dit(c(Lz+x),y,vs)+dit(c(x,y,Lz),S,vw)
Z10=optim(c(Lx,Ly),function(xy) f(xy[1],xy[2]),method='L')$value
route=c('OS','Z0','Z10','Y0','Y10','Z0','X10')
t=c(OS,Z0,Z10,Y0,Y10,Z0,X10)
m=min(t)
if(print) cat(route[which(t==m)],':',m,'\n')
invisible(m)
}
lds=seq(0,Ld,0.1)
plot(lds,sapply(lds,sim),bty='l',type='l',xlab='length of diagonal')
(opt=optimize(sim,c(0,Ld),maximum=TRUE))
opt$objective # �ŒZ�ł��K�v�ȕb��
(Scrit=opt$maximum*e) # �Œx�_�̍��WScritical
sim(opt$maximum,print=T)
# Z10
f<-function(x,y) dit(c(Lz+x),y,vs)+dit(c(x,y,Lz),Scrit,vw)
optim(c(Lx,Ly),function(xy) f(xy[1],xy[2]),method='L')
���ʂ́A�o�肳�ꂽ���w�ɓ��e���Ă����B
�v���O������()�̑Ή���R���}�ЂƂ̉ߕs���Ō듮�삷�邩���ρB
�܂��A���y�ł���Ă��邩��y�������ǔ[���̂���d�����Ƒ�ς��낤�ȁB
���ꑲ�ŗ��O���w�Ȃ�Đ������邗
���̗F�l�ŋ����𑲋Ƃ����F�l��
�����Ă�Ƃ�����������Ƃ����������B
���ƒ����m�[�g�͈�Ƃ�Ȃ��A�x�e���Ԃ�
�����̋����̂���{�⏬����ǂ�ł邗
�������Ԓ����J�n����30�����炢������
�������ɂ������ɂȂ��ĐQ�Ă��B
���̗ǂ����c���Ă����ȁB
�c�ɂȂ̂ŏm���Ȃ����A���ȏ��ȊO��
�����ĂȂ��āA���R�����狳�ȏ���
��ԗǂ��Q�l�����Ǝv���ƌ����Ă��ȁB
�����ȃ��c���������ǁA���͂ǂ����Ă�낤�H
���ȏ������ŋ����킯�Ȃ�����o�J���Ȃ��܂�
�x������
>>362
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c���� ���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�����P�O�̕��ʁi�ǁj�����������ꍇ�ɂ͂����O�̕ǂ�ʂ郋�[�g�Ƃ����O�̕ǂ�ʂ郋�[�g�̓������̂��������Ă����B
Lx=10; Ly=10; Lz=10 # �v�[���̑傫��
L=c(Lx,Ly,Lz)
Ld=sqrt(sum(L^2)) # �Ίp���̒���
e=L/Ld # �����P�ʃx�N�g��
vs=2 # �Ǐ㑬�xvelocity along side
vw=1 # �������x velocity in water
O=c(0,0,0) # �Ď����̈ʒu
dit<-function(X,Y,v) sqrt(sum((X-Y)^2))/v # X,Y�̈ړ����v���� distance->time
sim <- function(ld,print=FALSE){ # ld:���_��S(�Ίp����)�̋���
S=ld*e # swimmer�̈ʒu
# OS ������
OS=dit(0,S,vw)
# X0 (����x=0�������)
f<-function(y,z) dit(c(0,y,z),0,vs)+dit(c(0,y,z),S,vw)
X0=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method='L')$value
# Y0 (����y=0�������)
f<-function(x,z) dit(c(x,0,z),0,vs)+dit(c(x,0,z),S,vw)
Y0=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method='L')$value
# Z0 (����z=0�������)
f<-function(x,y) dit(c(x,y,0),0,vs)+dit(c(x,y,0),S,vw)
Z0=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method='L')$value
# X10 (����x=10�������) sqrt((Lx+y)^2+z^2)/vs == dit(c(Lx+y,z),0,vs)
f<-function(y,z) min(dit(c(Lx+y,z),0,vs),dit(c(Lx+z,y),0,vs)) + dit(c(Lx,y,z),S,vw)
X10=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method='L')$value
# Y10 (����y=10�������)
f<-function(x,z) min(dit(c(Ly+x,z),0,vs),dit(c(Ly+z,x),0,vs)) + dit(c(x,Ly,z),S,vw)
Y10=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method='L')$value
# Z10 (����z=10�������)
f<-function(x,y) min(dit(c(Lz+y,x),0,vs),dit(c(Lz+x,y),0,vs)) + dit(c(x,y,Lz),S,vw)
Z10=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method='L')$value
route=c('OS','Z0','Z10','Y0','Y10','Z0','X10')
t=c(OS,Z0,Z10,Y0,Y10,Z0,X10) # �e�ʂ���̓��B���Ԃ̂�����
m=min(t) # �ŏ��l�����Ƃ߂�
if(print) cat(route[which(t==m)],':',m,'\n') # �ǂ̌o�H����\��
invisible(m)
}
lds=seq(0,Ld,0.1) # �Ίp����̋����Ə��v���Ԃ��O���t�ɂ���
plot(lds,sapply(lds,sim),bty='l',type='l',xlab='length of diagonal')
(opt=optimize(sim,c(0,Ld),maximum=TRUE))
opt$objective # �ŒZ�ł��K�v�ȕb��
(Scrit=opt$maximum*e) # �Œx�_�̍��WScritical = �Ίp���㋗���~�����P�ʃx�N�g��
sim(opt$maximum,print=T) # �Œx�_�ɍő��œ��B����o�H��\��
# Z10(X10,Y10�ł����l)�����̌o�H
f<-function(x,y) min(dit(c(Lz+y,x),0,vs),dit(c(Lz+x,y),0,vs)) + dit(c(x,y,Lz),Scrit,vw)
optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method='L') # $par�������_��x,y���W
���w�ɓ��e����ƁA��������������ă��X�����̂Ŋy�����B
���_�l���o�����O�ɐ��������l�������������B
���l������������A���l�v�Z������������������������B
�Ԉ�����������Ђ�����Δ������ċɒl�v�Z���Ă��k�J�ɂ���邩��B
>>364
����ˁB
���Z�̓����ōs����g���ă��[�r�b�N�L���[�u��������l�Ԃ��������A���w�Ȃg��Ȃ��Ă�����Ɏ肪�����Ƃ������Ċ������Ă��܂��l�Ԃ������B
�ق�Ƃ��ɓ��̂����̂͗��w�����H�w���ɍs���B
�ق�Ƃ��ɓ��������̂������̂��h��ӃV���c���ł��邱�Ƃ͐\���グ��܂ł��Ȃ��B >>372
�o��҂��Ō��Wolfram���g�������l���������Ă�������A��͉���Nj�����̂͂�߁B
���̉����܂��܂��̋ߎ��B
> asin(h/r)*180/pi # ���_�l=60��
[1] 59.99515 ���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n�n
�܂��A�v���O�����ł̐��l���Ƃ��Ė����Ȓl���������B
�ŒZ���Ԃł̓����_�͑Ίp���̐^��ɂ͂Ȃ��Ƃ����͈̂ӊO�ł͂������ȁB
109 �����F�P�R�Q�l�ڂ̑f������[sage] ���e���F2020/02/03(��) 07:48:20.98 ID:0LuwDr/b [6/6]
>>107
�Ώ̐����炢����
Z=10�̕��ʂł̓����_��
�i6.074329 ,6.855617, 10)
�i6.855617, 6.074329 ,10)
�̓�����邱�ƂɂȂ�A
�ǂ�����o�R���Ă�
���v���Ԃ͓����ɂȂ�܂����i�܂��A���R�Ƃł��傤���ǁj
> f(jmpz$par[1],jmpz$par[2])
[1] 11.698156288555285
> f(jmpz$par[2],jmpz$par[1])
[1] 11.698156288555285
>
110 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2020/02/03(��) 08:21:54.06 ID:5QqjKgBu
���_�l��
11.69815627019646153787418090069489267584187319472412254855
�ł��B ���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
�����܂ł��Ɛ������ȁ@���N�������肩�`�@������҂ɂȂ�̂̓����݂�������w w w
20�N�ȏ���u�����N������ƍ��̈�w�͗����ł������ȁB�������X�����ς���Ă邵�ˁB���킢�������ȁ[
���Ԃ܂��̃����F���́@�����̊w�����Ⴂ���낤�� �B�����͂ǂ�ǂ�ς���Ă�������ȁB
�������o�C�g�I����Ă��ꂩ��X�e�[�L�n�E�X�Ɍ������B
>>379
�Δ����A���������������K�v������Ǝv�����̂����S���������ʼn�����Ƃ����B���ɂ̓v���O�����������E���ȁB �E�n�n�@�ʔ����Ȃ��܂��@�E�n�n
�v���O�������Ő����ł����̂ł��j����T�{�[���X�e�[�L�𒍕��B
>>392
�V���c�ぁ�������w�e�^�҂͍����ɂ�Ă���B �ǂ����@�X�e�[�L���܂����Hw w w w w w w
���䌧�z�O�s�Z�����@�X�e�[�L���܂����H�j���j��
��A�����炻��Ȃ�̃T�[�r�X������ˁB
��ŁA���ǂ����H
���������������܂�������w�悩������ �唚��
���A���͒����w��w���Ō�ȏo�g�̊Ō�t����[��
����A�h��ӃV���c������B
�t�F�����ɓ������Ȃ�����B
�������̊Ō�t�Ȃ玩���ł킩��Ȃ��Ă��������̈�t�ɕ����邩��B
>>401
��ŁA���ǂ����H
������h��ӃV���c��H�H ���̎͒�w���̐��P��2��3�������͂�߂ė~������
�h��ӃV���c��呲���Ă��ꂾ���
��ӎ�����呲��������w��w������i�ރX�� [�]�ڋ֎~](c)2ch.net
http://2chb.net/r/hosp/1424846816/695
695 ���O�F���̖���������[] ���e���F2016/09/25(��) 22:04:25.53 ID:FzuOCpqV
�����搶
���_��
��
1
�]��
�����o�ł��A�f���炵����t�����邵�A�����ł��A�ǂ����悤���Ȃ��̂�����B
����Ȃ̂́A�����܂Ōl�̎������Ǝv���Ă܂����B
���A
������a�@�i��t�̑啔�����A�������ӎ����j�ɗ��āA���̍l���͕ς��܂����B
�Ƃ���A�C�ɐH��Ȃ���t�̔��߂�T���_�����B���A���̏�ɃS�~��u���A�ȂǁA���w�����݂������点�����Ă����t�Ƃ����̂��A�͂��߂Č��܂����B
�����o�̕ϐl�����X�݂Ă��܂������A����ȁA���w���̃C�^�Y���݂����Ȃ��Ƃ�����l�́A���܂���ł����B
��͂�A��ӎ����́A����Ȃ�ȂƎv���܂����B
2016�N09��02�� 00��21��09�b ���䌧�z�O�s�Z�����@��x�K��Ă݂�@�������ł��H
��҂͂���Ȏ��Ԃɂ���ȂƂ���ŏ������ނ��Ƃ͂��܂���B���͒����w��w���Ō�ȏo�g�̊Ō�t����[��B������������[��B���n�n
����A�h��ӃV���c������B
�t�F�����ɓ������Ȃ�����B
�������̊Ō�t�Ȃ玩���ł킩��Ȃ��Ă��������̈�t�ɕ����邩��B>>406 �^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H
>>359
�ނ������̂́A�������𗧎������ŁA���̏ꍇ�Ȃ瓖����O�ŋ����Ă��炦�鎖���O�����ł͂����܂œ�����O�Ɏv���Ȃ����B
�{��ł͏��v���ԍő�ɂȂ�_��x=y=z��ɂ��鎖�������̂�������B
�Ƃ����w�E������Ă���̂ŁA������v���O����������Ă݂�B
�����l�������_���ɐݒ肵�Ď��������Ƃ��ɣx=y=z���������m�F�ł���悵�Ƃ���B # �����ɍł����Ԃ�v����_�i�Œx�_)��(w,w,w)�őΊp����ɂ��邩�̎���
rm(list=ls())
graphics.off()
Lx=10; Ly=10; Lz=10 # �v�[���̑傫��
L=c(Lx,Ly,Lz)
Ld=sqrt(sum(L^2)) # �Ίp���̒���
e=L/Ld # �����P�ʃx�N�g��
vs=2 # �Ǐ㑬�xvelocity along side
vw=1 # �������x velocity in water
O=c(0,0,0) # �Ď����̈ʒu
dit<-function(X,Y,v) sqrt(sum((X-Y)^2))/v # X,Y�̈ړ����v���� distance->time,v=1�Ȃ狗���Ɠ���
sim2 <- function(S,meth='Nelder',print=FALSE){ # ���_����S�܂ł̓����ŒZ���Ԃ�Ԃ�
# OS ������
OS=dit(0,S,vw)
# X0 (����x=0�������)
f<-function(y,z) dit(c(0,y,z),0,vs)+dit(c(0,y,z),S,vw)
X0=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method=meth)$value
# Y0 (����y=0�������)
f<-function(x,z) dit(c(x,0,z),0,vs)+dit(c(x,0,z),S,vw)
Y0=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method=meth)$value
# Z0 (����z=0�������)
f<-function(x,y) dit(c(x,y,0),0,vs)+dit(c(x,y,0),S,vw)
Z0=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method=meth)$value
# X10 (����x=10�������) sqrt((Lx+y)^2+z^2)/vs == dit(c(Lx+y,z),0,vs)
f<-function(y,z) min(dit(c(Lx+y,z),0,vs),dit(c(Lx+z,y),0,vs)) + dit(c(Lx,y,z),S,vw)
X10=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method=meth)$value
# Y10 (����y=10�������)
f<-function(x,z) min(dit(c(Ly+x,z),0,vs),dit(c(Ly+z,x),0,vs)) + dit(c(x,Ly,z),S,vw)
Y10=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method=meth)$value
# Z10 (����z=10�������)
f<-function(x,y) min(dit(c(Lz+y,x),0,vs),dit(c(Lz+x,y),0,vs)) + dit(c(x,y,Lz),S,vw)
Z10=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method=meth)$value
route=c('OS','Z0','Z10','Y0','Y10','Z0','X10')
t=c(OS,Z0,Z10,Y0,Y10,Z0,X10) # �e�ʂ���̓��B���Ԃ̂�����
m=min(t) # �ŏ��l�����Ƃ߂�
if(print) cat(route[which(t==m)],':',m,'\n') # �ǂ̌o�H����\��
invisible(m)
}
(opt=optim(par=sample(0:10,3),sim2,control = list(fnscale=-1),method='N'))
while(opt$convergence!=0){ #�@�����l�𗐐����������Ď�������܂ŌJ��Ԃ�
opt=optim(par=sample(0:10,3),sim2,control = list(fnscale=-1),method='N')
}
opt
opt$value # �ŒZ�ł��K�v�ȕb��
(Scrit=opt$par) # �Œx�_�̍��WScritical = �Ίp���㋗���~�����P�ʃx�N�g��
sim2(Scrit,print=T) # �Œx�_�ɍő��œ��B����o�H��\��
�����ł́A��������Ƃ���x=y=z���������Ă���B
> while(opt$convergence!=0){ #�@�����l�𗐐����������Ď�������܂ŌJ��Ԃ�
+ opt=optim(par=sample(0:10,3),sim2,control = list(fnscale=-1),method='N')
+ }
> opt
$par
[1] 7.436211 7.436219 7.436219
$value
[1] 11.69815
$counts
function gradient
296 NA
$convergence
[1] 0
$message
NULL
�Ⴂ���C��̏���Ɠ������Ă܁[���@�����y�����d�����Ă܁[��
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
>>419
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H �h��ӃV���c������B
�t�F�����ɓ������Ȃ�����B
�������̊Ō�t�Ȃ玩���ł킩��Ȃ��Ă��������̈�t�ɕ����邩��B
>>422
�t�F�����ɓ�������ƃt�F�����Ă��炦���B >>424
��R�L�����A�t�F�����`���R�ɂ��ă`���R�����炤�ɂ�
�Ƃ������ɂ����珬�w���ł������邩���ˁB ���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
>>413
���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�t�F�����Z���Y�����D���Ȃ́H >>372
�Δ������Ă݂��B
route Z0
t=��(x^2+y^2)/2+��((p-x)^2+(q-y)^2+r^2)
d/dx(1/2 sqrt(x^2 + y^2) + sqrt((p - x)^2 + (q - y)^2 + r^2)) = x/(2 sqrt(x^2 + y^2)) - (p - x)/sqrt((p - x)^2 + (q - y)^2 + r^2)
d/dy(1/2 sqrt(x^2 + y^2) + sqrt((p - x)^2 + (q - y)^2 + r^2)) = y/(2 sqrt(x^2 + y^2)) - (q - y)/sqrt((p - x)^2 + (q - y)^2 + r^2)
route X10
t=��((10+y)^2+z^2)/2 + ��((10-p)^2+(q-y)^2+(r-z)^2), (y<z�̂Ƃ�)
d/dy(1/2 sqrt((10 + y)^2 + z^2) + sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)) = (y + 10)/(2 sqrt((y + 10)^2 + z^2)) - (q - y)/sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)
d/dz(1/2 sqrt((10 + y)^2 + z^2) + sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)) = z/(2 sqrt((y + 10)^2 + z^2)) - (r - z)/sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)
t=��(y^2+(10+z)^2)/2 + ��((10-p)^2+(q-y)^2+(r-z)^2), (y��z�̂Ƃ�)
d/dy(1/2 sqrt(y^2 + (10 + z)^2) + sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)) = y/(2 sqrt(y^2 + (z + 10)^2)) - (q - y)/sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)
d/dz(1/2 sqrt(y^2 + (10 + z)^2) + sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2)) = (z + 10)/(2 sqrt(y^2 + (z + 10)^2)) - (r - z)/sqrt((10 - p)^2 + (q - y)^2 + (r - z)^2) �����˂��@�����˂��@�ł��ˁ@��������Ȃ�@�唚�I
�J���t�@�����X�O�@��ǂŌ��Ă��[�@���鏗�オ�@���̐l�v����ɂȂɂ��������́H����������@�����Ă�w
>>434
���̏��オ��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�t�F�����Z���Y�����D���Ȃ́H ���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ́H
�ǂ����H
>>434
��ǂɃt�F�����ɑ����ł��铪�]�͂Ȃ��́H
�݂�ȗ������w�Ȃ̂��H �������w�ő��Ƃł���A������
���Ƃł��Ȃ��Ƃ��A�����ʂ�Ȃ��Ƃ��A���w�������̂ł́H
>>438
�n���𗠌����w�����ė��N�����Ď��Ɨ����҂����N�r�W�l�X���f���ʼn҂��̂��V���c���ł���B �h��ӃV���c���̈�ǂ̓t�F�������������Ȃ��h��ӓ��]���炯�̂悤���B
�܂��A�Z���Y����]�̉\�������邪�A���������̂͂��̂��������ˁB
�̂Ƃ������A���̈ꎞ���͈�҂ɂȂ�Ղ�����
��t�s���̒��œ��w����o�J�ł��K����t�ɂȂꂽ
��������������������Ɩ������ē��w������o�J�e�������̂��낤
�ł����w�҂̒��ň�҂ɂȂ�Ȃ��z��قǂǂ����悤���Ȃ��l�Ԃ͂��Ȃ�
�g�����ɂȂ�Ȃ�����
���R����z�M����Ă����̂����A�ŋ߂̍������Ĕn������҂ɂ����肾�炯���ȁB
��112���t������聟
���₯�̗U���ƂȂ�ɂ����̂͂ǂꂩ�B
����112-��112���t���Ǝ�����������i��w�]�_�Ёj���o��@�w��������80.2��
A �ߐH
B �^��
C �얞
D �����b�H
E �O���p��
�������������o���āA�������w�̃V���c��w����r�����ׂ����Ǝv����Ȃ��B
1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A1����2�i���邱�Ƃ͘A�����Ȃ����̂Ƃ���B15�i�̊K�i�����鏸����͉��ʂ肠�邩�����߂�B
�����̃V���c��̓t�F�����ɂ������o���Ȃ��m�b�x��B
�������w�Ȃ낤�ȁB
>>441
�����l���s���̂�������w�̗��w����H�w��
�����Ȃ����ǃA�z�ł��Ȃ��̂��s���̂�������w��w���i���Ⴊ���j
�A�z�����s���Ȃ��̂��h��ӃV���c���B
�t�F�����ɓ����o���Ȃ��Z���Y���W�c�ł��邱�Ƃ����������˂� ## �I�����s�b�N
"�I�����s�b�N�T�C�Y�E�v�[��50m�~25m�̐��̓������v�[���̈�̊p�ɊĎ�����u���B
�Œ�2.0 m (6 ft 7 in)�A3.0 m (9.8 ft)�����������
�Ƃ������ƂȂ̂ŁA���[2.5m�Ƃ���B
���̊Ď����͐��E�L�^�ňړ�������̂Ƃ���B
���j100m���R�` 46�b91�Ő������ړ�
����100m9�b58�Ńv�[���T�C�h���v�ړ�
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b�K�v���v�Z����B
"
rm(list=ls())
graphics.off()
Lx=50
Ly=25
Lz=2.5
L=c(Lx,Ly,Lz)
vs=100/9.58 # �Ǐ㑬�xvelocity along side
vw=100/46.91 # �������x velocity in water
Ld=sqrt(sum(L^2)) # ���̑Ίp���̒���
e=L/Ld # �����P�ʃx�N�g��
O=c(0,0,0) # �Ď����̈ʒu
dit<-function(X,Y,v) sqrt(sum((X-Y)^2))/v # X,Y�̈ړ����v���� distance->time,v=1�Ȃ狗���Ɠ���
sim <- function(S,meth='Nelder-Mead',print=FALSE){ # ���_O��S�ւ̓��B���Ԃ�Ԃ�
if(!all(0<=S & S<=L)) return(0) # S���v�[���O�̍��W�Ȃ�0��Ԃ�
# OS ������
OS=dit(0,S,vw)
# X0 (����x=0�������)
f<-function(y,z) dit(c(0,y,z),0,vs)+dit(c(0,y,z),S,vw)
X0=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method=meth)$value
# Y0 (����y=0�������)
f<-function(x,z) dit(c(x,0,z),0,vs)+dit(c(x,0,z),S,vw)
Y0=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method=meth)$value
# Z0 (����z=0�������)
f<-function(x,y) dit(c(x,y,0),0,vs)+dit(c(x,y,0),S,vw)
Z0=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method=meth)$value
# X10 (����x=10�������) sqrt((Lx+y)^2+z^2)/vs == dit(c(Lx+y,z),0,vs)
f<-function(y,z) min(dit(c(Lx+y,z),0,vs),dit(c(Lx+z,y),0,vs)) + dit(c(Lx,y,z),S,vw)
X10=optim(c(Ly/2,Lz/2),function(yz) f(yz[1],yz[2]),method=meth)$value
# Y10 (����y=10�������)
f<-function(x,z) min(dit(c(Ly+x,z),0,vs),dit(c(Ly+z,x),0,vs)) + dit(c(x,Ly,z),S,vw)
Y10=optim(c(Lx/2,Lz/2),function(xz) f(xz[1],xz[2]),method=meth)$value
# Z10 (����z=10�������)
f<-function(x,y) min(dit(c(Lz+y,x),0,vs),dit(c(Lz+x,y),0,vs)) + dit(c(x,y,Lz),S,vw)
Z10=optim(c(Lx/2,Ly/2),function(xy) f(xy[1],xy[2]),method=meth)$value
route=c('OS','Z0','Z10','Y0','Y10','Z0','X10')
t=c(OS,Z0,Z10,Y0,Y10,Z0,X10) # �e�ʂ���̓��B���Ԃ̂�����
m=min(t) # �ŏ��l�����Ƃ߂�
if(print) cat(route[which(t==m)],':',m,'\n') # �ǂ̌o�H����\��
invisible(m)
}
(opt=optim(par=c( # �����l�͗������������čő�ƂȂ���W�Ə��v���Ԃ�T������
sample(seq(0,Lx,le=101),1),
sample(seq(0,Ly,le=101),1),
sample(seq(0,Lz,le=101),1)),
fn=sim, control=list(fnscale=-1),method='Nelder-Mead'))
(opt_scrit=optim(par=c(49,23,1.3),fn=sim,control=list(fnscale=-1),method='N')) # ���m�̍Œx�_
opt_scrit$par/e # ���̑Ίp����ɂ����3�v�f�����l�ɂȂ邪�A�Ȃ�Ȃ����Ƃ��m�F
search <- function(){
opt=list(convergence=1,value=0) # �T���̂��߂ɏ����l�͎������Ȃ������l�i0�ȊO)�ɐݒ�
while(opt$convergence!=0 | opt$value < opt_scrit$value){
(opt=optim(par=c(
sample(seq(0,Lx,le=101),1),
sample(seq(0,Ly,le=101),1),
sample(seq(0,Lz,le=101),1)),
fn=sim, control=list(fnscale=-1),method='Nelder-Mead'))
}
return(opt)
}
options(digits=22)
search() # lengthy process
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���Ēn�ʋ�������P ���̏��̋K��ɏ]�����Ƃ������Ƃ��āA���O���́A���O���R���̍\�����y�ьR�����тɂ����̉Ƒ��ł���҂���{���ɓ���邱�Ƃ��ł���B
�Q ���O���R���̍\�����́A�����y�э��Ɋւ�����{���̖@�߂̓K�p���珜�O�����B
���O���R���̍\�����y�ьR�����тɂ����̉Ƒ��́A�O���l�̓o�^�y�ъǗ��Ɋւ�����{���̖@�߂̓K�p���珜�O�����B
�������A���{���̗̈�ɂ�����i�v�I�ȋ������͏Z����v�����錠�����擾������̂Ƃ݂Ȃ���Ȃ��B
D[Sqrt[x^2 + y^2]/2 + Sqrt[r^2 + (-p + x)^2 + (-q + y)^2], x]=0
D[Sqrt[x^2 + y^2]/2 + Sqrt[r^2 + (-p + x)^2 + (-q + y)^2], y]=0
���䌧�z�O�s�Z�����@�ǂ����ȁH
�ӂӂ�
�����@����������肾�� w ���S������B���肪�Ƃ��B
x/(2 Sqrt[x^2 + y^2]) + (-p + x)/Sqrt[r^2 + (-p + x)^2 + (-q + y)^2]=0
y/(2 Sqrt[x^2 + y^2]) + (-q + y)/Sqrt[r^2 + (-p + x)^2 + (-q + y)^2]=0
���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ́H
�ǂ����H
�����̃V���c��̓t�F�����ɂ������o���Ȃ��m�b�x��B
�������w�Ȃ�B
>>454
�t�F�����ɓ����o���Ȃ��Z���Y���j���I�}�G�ȁB
�h��ӃV���c���ɗ������w�Ȃ�H ���撣���I��w���������ł͂����̈�ʐl������˂� w
���_�����ƒ�w�͂��v���I�������ˁB�c�O��������w
>>460
�c�O�Ȃ̂̂̓I�}�G�̓��B
���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ́H
�ǂ����H >>459
�����ɑ��l�肵�Ă���ǃA�z���I�}�G����B
�܂��ɍ������݂̓��]���ȁB
�����܂ŃA�z������A���c�����}����H
�t�F�����̓������Ȃ��́H
�N���ɕ����Ă��������B
���͂��h��ӓ��]���炯�Ȃ̂��H ���~�����ˁB����Ȃɐ��s�ׂ������Hw �җ�߂��̂ɂ� w �������ɑ��肳��Ȃ��j�̓T�^����w w
���䌧�z�O�s�Z�����@�����܁[�������肩�B��w�͂ق��Ƃ��Ă��邯�ǂȁB�����������̂��ƃA�_���g�r�f�I�̒j�D�ɂȂ邵���Ȃ���ˁHw���~�������� �n�n�n�@�������N�Ŋҗ�����܂� w w w
�����@���܂� w���a������B�����D���Ȑl�����ɖ��f�ɂȂ邩���w
>>465
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B
�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H >>463
��ŁA�t�F�����̓��͏o���Ȃ��́H
���ƃ`���R�̖��ɂ���������̏��w���ł��������Ȃ��́H �֓��𒆐S��HIV �~�ł̊������L�����Ă���B�������ł͒����l�̗��p�������ėv���ӂƂ̂��ƁB���Ɋi���X�͊�Ȃ��B
�L�X��I�[����SEX�ł���������B
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B
�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
>>468
�����͊i���X����Ȃ��̂ɑ���
�h��ӃV���c���ł͊w������Ƃ��قǔn�������B
���ǂ����H �t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɕς��悤�B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B
�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
> yu = function(V=500,T=65,C=7,H=98) V*(T-C)/(H-C)
> YU=sapply(0:30,function(x) yu(C=x))
> rbind(0:30,round(YU))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18]
[1,] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
[2,] 332 330 328 326 324 323 321 319 317 315 312 310 308 306 304 301 299 296
[,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30] [,31]
[1,] 18 19 20 21 22 23 24 25 26 27 28 29 30
[2,] 294 291 288 286 283 280 277 274 271 268 264 261 257
���R����B�v���C�}���[�o�����X�n���̈��{�C���o�E���h�O�݊l������̂������œ��{�{���{������B
�ږ���ό������͊m���ɉu�a���������܂�邩��f�����b�g�̕����傫���Ƃ���قnj����Ă��̂ɁA���{�́u�����������Ɂv�ł��̗L��l�B
��ӈ�呲�ɐf�Ă��炤���ċ��낵����
��f�C��f�̘̂A����������
taxi <- function(x,F,D,C,B){ # F:����^�� D:����苗�� C:���Z���� B:���Z����
if(x<=D) return(F)
else F + C*ceiling((x-D)/B)
}
taxi(27100,F=500,D=1200,C=100,B=264) # ���}���A���i��ȑ�w���瓌���w�܂ł̃^�N�V�[����
taxi(27100,F=420,D=1052,C=80,B=233) # �����w���琹�}���A���i��ȑ�w�܂ł̃^�N�V�[����
>>475
�i�������œ���������Ɛ��{�Ԃ���悤�Ȃ��̂���B
���{�ŋ��낵���̂͊w�������w���قǔn������������ˁB �������A���b��傠����͒����x���H
���x���J��Ԃ��Đ��s�����ǂɜ늳���Ă���ƔA����ፍ������ĔA��������N�����B�������A���K�v�ɂȂ����ꍇ�̓J�e�[�e���������Ȃ��đ�ςȂ��ƂɂȂ邼��w
�~�ł�HIV�̓V�����ɂȂ��̂Ō��������ق��������� w
�������ꂩ��ȕ�����̓`���|�R���Ă���`���|�R�͂킩�邻������[��@�J�J�J w
B�́@C�́@���|���� �[�a�C�̃`���|�R�͌����ˁ[��������͂قƂ�lj����a�C�������Ă���@���̒��ɂ��� w
�����x������ w
�A���̉��ɃR���W���[�}���������Ƃ��͂т����肵�����㋉��ɕ�������悭����Ƃ̂��� w
�t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɕς��悤�B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B
�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
>>483
�h��ӃV���c�̏㋉��ɑ��k���Ă��������B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H >>482
�h��ӃV���c��͓��̒��ɋ@�\�s�S������Ă���B
��R�L���ɓ����邱�Ƃ��ł��Ȃ��B �|���V�F���U�͗��ꑲ�����̂悤����
�h��Ȏ����Ȃ̂ŁA�Ă����莄���ォ�Ǝv���Ă�
�ǂ����ɂ���n���ȓz���@���ׂĂ�_�ɐU���Ă�
��}���Č����J���ψ����C���t�����[�@��ߎw��O�|�������������Ă������Ǎ������{�����ɊJ���Ȃ������K�v�Ƃ��b���ʂ��ĂȂ��q���̌�����œ˂��ς˂��
���ǎ����̂����Ńp���f�~�b�N�ɂȂ肻���Ȃ̂ɐӔC�C�����ꂻ���Ȃ��̖�}�H
>>481
�I�}�G���h��ӃV���c�������w�Ȃ͕̂��͂ł킩�邼�B
��R�L���͉��������H
��R�L���Z���Y����]��Ȃ̂��H ���܂��@�A���y������B�Ȃ����Ă邼�@����w
��A���������Ɣ^���o��@�j���[�L�m�����ϐ��̐��a�����s���Ă邼���@�ЂЂ�
>>492
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
���̓����o���Ȃ��́H�Z���Y����]��Ȃ̂��H
����Ƃ��h��ӃV���c���̌��C��̓E���R���Ă������Ȃ������R�L���Z���Y����I�������̂��H
��ŁA���ǂ����H >>487
����A�h��ӃV���c��呲�Ƃ��������������o���Ĕ��������A
>���ׂĂ�_�ɐU���Ă�
�ɊY������Ǝv���B
��Z�Ɍւ肪���ĂȂ����瑲�Ƒ�w���疼���Ȃ��̂��݂�悭������B �^�N�V�[�������オ�����̂ʼn^����r�̃O���t���쐬����
# ���^���i���^)
F1=640 # ����^�� Fair
D1=1500 # ����苗�� initial Distance
C1=90�@ # ���Z�^�� Charge by distance
B1=345 # ���Z���� charge By distancce
# �V�^��
F2=660
D2=1500
C2=90
B2=331
# �^�����狗���i���^��)�@fare to distance by old system y:\
f2d.o <- function(y,F=F1,D=D1,C=C1,B=B1){
if(y<F) return(0)
D+(y-F)%/%C*B
}
y=seq(0,5000,by=10)
plot(y,sapply(y,f2d.o),type='l',bty='l',xlab='������(�~)',ylab='���B����(m)')
# ��������^��(�V�^��) distance to fare by new system
d2f.n <- function(d,F=F2,D=D2,C=C2,B=B2){ # F:����^�� D:����苗�� C:���Z�^�� B:���Z����
if(d<=D) return(F)
else F + C*ceiling((d-D)/B)
}
# ���^������V�^��
f.o2n <- function(y){ # old fare to new fare
if(F1<=y & y<=F2) return(F2)
d2f.n(f2d.o(y))
}
# ���ymax�~�܂ł̉^���ω��O���t
ymax=10000
(ymax=F1+C1*(ymax-F1)%/%C1) # ymax�ȉ��ŕ���
y=seq(F1,ymax,by=C1)�@�@�@�@# ���^���̌��̂ݗ�
z=sapply(y,f.o2n) # �V�^�����Z�o���ăO���t��
plot(y,z,type='p',pch=19,bty='l',xlab='������',ylab='�V����') ;�@points(y,y)
segments(y,y,y,z)
r=(z-y)/y*100
plot(y,r,bty='l',pch=19,xlab='���^��',ylab='�l�グ��(%)')
y[which.max(r)]
f.o2n(730)
r[2]
�����A�����@�Ȃ��Ȃ�����܂���@�A���̕s����������w
�`���|�R���V�S���Ɖ��ǂ�����Ȃ����� w�Ǖ������Âɂ��邵���Ȃ������܂��͗������Ȃ�����I�i�j�[�����Ⴄ���� w
��490-492�@�̓��e���݂�ƁA�h��ӃV���c��̃I�c���̏o������Ɏ��悤�ɂ킩��Ȃ��B
��R�L���̓����o����悤�ȓ��]����Ȃ��ˁB
�ЂЂЁ@�����Ƃ����Ƃ���[��@�ЂЂ�
�����ɑ��l�肵�Ă���ǃA�z���I�}�G����B
�܂��ɍ������݂̓��]���ȁB
�����܂ŃA�z������A���c�����}����H
��R�L���ɂ܂��������Ȃ��́H
�n���Ȃ�B
����ɋ����Ă����l���Ȃ��́H
�݂�ȗ����o�J���炯�H
>>501
�{���ɂ���ł��Ȃ��n���Ȃ́H
����ő�w��������ė������w�Ȃ낤�ˁH
�t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɕς��悤�B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B
�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
���A�ǂ����H ���ō����ɍ��i�ł��Ȃ��́H�D�G�ȓ��]�Ȃ�H�t�n�n�n�n
>>505
�Ƃ����ɒʂ�����B
�E���ƃv�V�R���I���w��̔N�ɁB
�ǂ��������������Ȃ��Ȃ�����y���������B >>505
�t�F�����̓��܂����H
�ʃX���Ń`���R�ƈ��̖��ɂ����璼���ɐ������ꂽ�̂�
�����ł������ł�̂��O��Ŗʔ�������t�F���Ǝ�R�L�ɂ����̂ɁB
�I�}�G�̓��]����A�ꐶ�Z���Y����]�����B
�ǂ����Ȃ炻��Ȃɔn���ȂH �t�t�t�@�����s���i�̐��_�a���҂ł͂ȁ[�@��Q�Ҏ蒠�ʼn��Ƃ��H���Ă����邾�낤�@�悩������ w
�����Ȃ��Ă����@�Q��@����������J���t�@�����X�Ȃ̂���@�U��҂���@�n�n�n�n
>>508
�t�F���������������Ȃ�
�m�b�x��̐��_��Q�̓I�}�G����B
��ŁA���ǂ����H ����ł�����ƃO���t����ėV��ł݂邩�ȁB
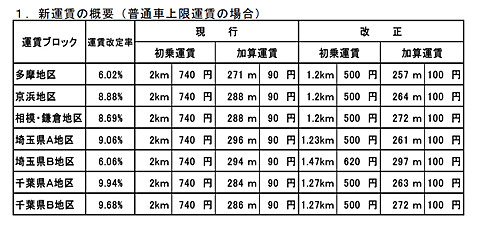
>>509
�J���t�@�̎Q���҂Ƀt�F�����������Ă��炦��B
�����V���c�ゾ�炯�Ȃ疳������ˁH >>505
�t�F�����̓��܂����H
�ʃX���Ń`���R�ƈ��̖��ɂ����璼���ɐ������ꂽ�̂�
�����ł������ł�̂��O��Ŗʔ�������t�F���Ǝ�R�L�ɂ����̂ɁB
�I�}�G�̓��]����A�ꐶ�Z���Y����]�����B
�ǂ����Ȃ炻��Ȃɔn���ȂH
���c�����}�ł����Ă�H ���{���ό��ŊO�݂��҂��Ȃ�Ė����Șb�B
�M���V�������Ċό�����҂���Ȃ�����j�]��������B
���{�̓��m�Â���̍��Ȃ����A�����݂����ȊC�O�̍H�ꗊ��
����Ȃ��č����ł��႟�����B
�S�~�݂����ȊO���l�ق������{�l�̌ٗp���������肵��B
�z���g���������}�̓A�z�����B
�������ȁB
�����ʏ�ɖ����ɑ����A1�I�[���̒�R�ō��ꂽ�����`�̊i�q�ɂ����āA
�i�C�g�̓���(�j�n���)�̈ʒu�ɂ���2�̃m�[�h�Ԃ̒�R��
4/��-1/2 �I�[���ł��邱�Ƃ������B
�iGoogle���Ў��� - ��Փx�������邽�߂Ɉꕔ�ȒP���j
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
>>511
�^���������̎Z�o���@�͕s�����ȁB ���\�����炱���������艺�낳��Ȃ���
�ꉭ�ܐ疜�~�͂���邵�A�S���̘d�G����Ă��Ԃ��N�i����Ȃ���
�������Ă������Ă���邵�A������Ă������Ɛ������Ȃ��Ă����������Ȃ����炵�Ȃ��ėǂ���
����ȕ֗��Ȑl���g�b�v�Ȃ�A���͂�肽������o���邩��
�܂��A����̌��́@���́@����@�ɂ͂Ȃ�\�������邯��
���{���k�Ђ̂Ƃ��ɂ�������ƂƂ����ΐ����l�̃f�}���������Ƃ������

> ���{���k�Ђ̂Ƃ��ɂ��������
�Ƃ��������{�A�����ꖡ�ƃl�^�j�A�t���k�Ђ��������w
���\�����炱���������艺�낳��Ȃ���
�ꉭ�ܐ疜�~�͂���邵�A�S���̘d�G����Ă��Ԃ��N�i����Ȃ���
�������Ă������Ă���邵�A������Ă������Ɛ������Ȃ��Ă����������Ȃ����炵�Ȃ��ėǂ����A��l���A�N���o�b�g�i��ň��{�ɑ݂�������Ă�肽������������ł���B
����ȕ֗��Ȑl���g�b�v�Ȃ�A���͂�肽������o����B
�R�s�y�����A���{�̍s�����Ă��̗\�z�ʂ肾�ȁB
���{�����������Ă����܂œ��{�ׂ̈ɓ����Ă����C���[�W���N����B
�����I�ɔᔻ����郊�X�N���w�E���ꂽ�瑬�U���~�߁��x���g�X�ɒx���A�Ƃ�
���ʂɂ������Ǝv���B
------
�i��
�����������@�̏�̃w���|�[�g����w���ŕ������̂ق��Ɍ��n���@�ɍs����܂��B
���̎��@�Ɋւ��ĕł́A�}�슯�[�������܂߂Ă��̎��_��
�������s���ׂ��ł͂Ȃ��ƁA���������悤�ȐT�d�_�A���Θ_���o���Ƃ����ӂ���
�����Ă���܂����A�ǂ��������R�Ŕ����ꂽ��ł��傤���B
�}��
���́A�{���_�Ƃ��Ă͍s�����ق��������ł��傤�˂ƁB
�����ǐ����I�ɂ͖��炩�Ƀ��X�N�ł��ƁB
�����s�������Ƃɂǂ�ȈӖ������������āA����ȂƂ��ɑ�����
�̂��̂�
�o�����Ă����đ��������������ƁA
�ォ���ΐ����I�Ȕᔻ������܂��ƁB
������s���ׂ����Ⴀ��܂���ƁA���͎~�߂܂����B
�������琛���ǂ����������Ƃ����ƁA
�u�����I�Ɍォ�����邩�ǂ����ƁA���̋ǖʂł����ƌ��������Ƃ��R���g���[���ł����
�Ƃǂ������厖�Ȃv�ƌ�������A
�u�킩���Ă���Ȃ�ǂ����v�ƌ����܂����B
�����������̓Ɨ����؈ψ���@�q�A�����O
https://apinitiative.org/wp/wp-content/uploads/2012/07/3b328846ead37ec0bd01e9b8a83db762.pdf >>525
�����͓������B
�J���t�@�̎Q���҂Ƀt�F�����������Ă���Ȃ������̂��H
����ς�A�����V���c�ゾ�炯����B �{���ɂ���ł��Ȃ��n���Ȃ́H
����ő�w��������ė������w�Ȃ낤�ˁH
�t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɕς��悤�B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
���A�ǂ����H
���낻��@�����オ�@�����͏��ƃf�[�g�I�Ƃ������o�����I
�킴�킴5ch�ŕ��Ȃ��Ă������Ǝv������
����a�@�̈�t�͈Ǘт����肾��
�����͗ǂ��{��A�ǂ��{�邱��
�����ɍ���
������SEX�͋C�����悩�����ȁ`�ޏ����X�P�x�ŋ���������B�n�n�n�n
>>530
�{���ɂ���ł��Ȃ��n���Ȃ́H
����ő�w��������ė������w�H
�t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɂ������B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
���A�ǂ����H �����͂��̃V�~�����[�V�����������ł����̂ŋC���������B
�u�����̃N���[�Y�D�ł�
�D���̊��C�����ʂ炵������13����ɔ��ǂ����z������Ƃ��̋߂��̕����̂�̓v���X��14���u�����Ȃ��Ƃ����Ȃ�
���ꂪ���̑D���̏Ƃ����B
����Ȗ����l���Ă݂��B
���ׂ̂ǂ��炩������������14�������A1���Ŋ�������m��p��1%
�����̔z�u�͒����`�i�܂�n�܂���I�����Ȃ��j�B
���ǂ��邩�A�u�����Ԃ��I���Ή��D�ł���B�q�Ə斱�������킹���l��n��3000�l�B�N���[�Y�D����S�����D�ł�������̊��Ғl�́H
>>530
�h��ӃV���c��̓Z���Y����]����˂��́H �I�i�j�[�͂������N���ĂȂ��ȁ`�ޏ���炵�ĂȂ���ˁB��҂ɂȂ��Ă悩�����ȁB�����e���e�ł� w
>>534
����A����ɓ������Ȃ����O�̓Z���Y����]����B
�{���ɂ���ł��Ȃ��n���Ȃ́H
����ő�w��������ė������w�H
�t�F���͊������X�N������Ƃ����w�E�Ȃ̂Ŏ�R�L���ɂ������B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�N���ɑ��k���Ă��������B�I�}�G�̎���ɂ̓h��ӓ��]�������Ȃ��̂��H
���A�ǂ����H �h��ӃV���c�ゾ�Ƃ��������̂��ł��Ȃ��̂͗������w������d�����Ȃ����Z���Y�����ɓ����o���Ȃ��̂̓Z���Y�����߂��œ���������Ă��邩�炶��˂��́H
���̃X���̃h��ӃV���c�ぁ�Z���Y����]��
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����m���ɐ����҂ƒf��ł�����̂�S�ċ�����B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v
���鏬�w�Z�̂���N���X�ł́A�o�X�ʼn����ɍs�����ƂɂȂ����B
�o�X�̍��Ȃ͎��O�Ɍ��܂��Ă������A�ŏ��Ƀo�X�ɏ���������������̍��Ȃ�Y��āA�C�ӂ̍��Ȃɍ����Ă��܂����B
���̎����́A��l���o�X�ɏ�荞�݁A�����̍��Ȃ��Ă�����̍��ȂɁA�����łȂ���Ă���C�ӂ̍��Ȃɍ������B
���̂Ƃ��A�Ō�̎����������̍��Ȃɍ����m���́A�N���X�̎������ɂ�����炸���ł��邱�Ƃ��ؖ�����B
seat.n <- function(n){ # n: ���k�̐l��
s=1:n # �c����Ȕԍ�
s1=sample(s,1) # �ŏ��̐��k�P�̍���Ȕԍ�s1
s=s[-s1] # s1���c����Ȃ��珜��
for(i in 2:(n-1)){ # ���k�Q���琶�kn-1�܂�
if(i %in% s){ # ���ki�̍���i���c���Ă����
s=s[-which(s==i)] # ���̍��Ȃ�s���珜��
}else{
ls=length(s) # �c����Ȑ� length of s
si=sample(ls,1) # 1:ls�̒�����1�I��si�Ƃ���
s=s[-si] # si�Ԗڂ̍��Ȃ�����
}
}
s==n # ���k���̐Ȕԍ��͂����̐^�U��Ԃ�
}
sim <- function(n,k=1e4){
mean(replicate(k,seat.n(n)))
}
�����l����̊ό������ɖڂ������ō����̐������댯�ɂ��炷���{�W�O����
�ʂ��o�Ă��邩��Ǝq���𒓎ԏ�ŏ����Ă��ɂ��Ă���p�`���J�X��������B
��͂�A���P�̒�ӃV���c��w�����������ᐊ�ނ���킯���B
��������A�������}�X�N�𒆍��ɂ�����
�����̍H��ғ���~�œ��{�ő���Ȃ�����g�p�T�������
�ǂ�ȃR���g����
�ŏ��Ƀ}�X�N�𒆍��ɑ���͍̂\��Ȃ���A���̎��͔�r�I�ɗ]�T�������������Ă�����݂��Ă��̂��l��
�ł����̌�ɔ�����߂ɂ��]���⒆���l�ɂ�锃����߂��m�[�K�[�h���Ă��̂�
���̊��ɋy��Ŗh�앞�Ȃǂ𒆍��ɑ��낤�Ƃ���p���͂����Ȃ���
���ꂩ����l����Ɠ��{�ɂ��h�앞���K�v�ƂȂ���瓖�R�̘b
�N���[�Y�D�Ɋ֗^����l�炪�}�X�N�Ǝ�܂������Ăǂ����Ƃ�������
�����Q���ڂ��[�݂�Ȋ撣���ė~�����ȁ[�n�n�n�n
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
��҂ɂȂ�Ȃ��Ă���������Ȃ����@�ʂ̓��������I
>>544
�����牽��
�m��Ȃ������̂�w
�����o�J���� rm(list=ls())
p=rev(seq(0.55,1,by=0.05))
p
f=function(x) x+sample(c(1,-1),1,prob=c(p[x],1-p[x]))
i=0
x=1
while(x<10){
x=f(x)
i=i+1
}
i
�o�Z�̖��
�E���_0����10�}�X��ɃS�[��������B�}�X���Ƃɖ�Ԃ�����B
�E1�^�[����1�}�X�i�߂邪�A��Ԃɕ������1�}�X�߂�B
0�}�X�ڂ̏���100%
1�}�X�ڂ̏���90%
2�}�X�ڂ̏���90%
3�}�X�ڂ̏���85%
4�}�X�ڂ̏���85%
5�}�X�ڂ̏���85%
6�}�X�ڂ̏���85%
7�}�X�ڂ̏���75%
8�}�X�ڂ̏���65%
9�}�X�ڂ̏���55%
�E10�}�X�ڂɓ�������ɂ͕��ω��^�[���|����̂ł��傤���H
>>545
�h��ӃV���c�̃Z���Y����]���
�Z���Y�����̓��͂܂����H
�h��ӃV���c�𗎂Ƃ����Ƃ��č����ɏo�邼�� �����͋v���Ԃ�̋x���Ȃ̂Ō��C��̔ޏ��ƃ}���\��SEX���B�w�g�w�g�ɂȂ��Ă������y�����B�t�[
���т��ꂩ��H���B���[���T�[�r�X�ŃT���h�E�B�b�`�H�ׂ悤���ƁB���ɔޏ������ĐQ�Ă�B
�~�[���ł���I
�~�[�������㑲�ł�����
5ch���Ȃ��珗�����Ă܁[���I
��˂��A�ꏑ�����Ł[��
�ޏ��A���x���ǂ��Ȃ����ȁB�v���C�����낢�닳���������肭�Ȃ����B
��������N�̂S���B
����\�����Ă���ȁB

���{�ō��w��̃V���c���i�w������Ƃ��قǒ���l�̌X�������邗�j�ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
http://2chb.net/r/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���ƕK�v�Ȋw��̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƃ��̏ꍇ�Ɏx�������w��̊��Ғl�����߂�B ���{�ō��w��̃V���c���i�w������Ƃ��قǒ���l�̌X�������邗�j�ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
http://2chb.net/r/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���ƕK�v�Ȋw��̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƃ��̊w�N�A���̏ꍇ�Ɏx�������w��̊��Ғl�����߂�B ���킢��������Ă�̂ɐ������Ƃ���ȁB�]�N�]�N���邭�炢�C���������B�X�^�C���ǂ��@���l�����@�F���Ł@���܂��@���x�̓��[���v���C�����Ă݂悤�I
>>557
>>545
�h��ӃV���c�̃Z���Y����]���
�Z���Y�����̓��͂܂����H (p=1-c(10,16,34,9,10,26)/125)
t1=12145000 ; t2=7030000
tu <- function(n) t1 + t2*ceiling(n-1)
f <- function(xy){ # xy:c(�w�N,�i������)
x=xy[1] ; y=xy[2] # x:�w�N y:�i������x�Ȃ�1,���N����x�Ȃ�0
z=sample(1:0,1,prob=c(p[x],1-p[x])) # �i������
if(y==0 & z==0){ # ��N�Ȃ�
return(c(x,2)) # c(���N�w�N,2)��Ԃ�,2:�ފw�ő��Ƌ��
}else{
return(c(x+z,z)) # c(�i���w�N,�i������)
}
}
sim <- function(print=FALSE){ # �݊w�N��,�ŏI�w�N,�i�������Ԃ�
xy=c(1,1) # �V����(1�N��,���N�Ȃ�)
i=0 # �݊w�N��
while(xy[1]<7 & xy[2]!=2){ #���ƑO���ފw�łȂ����
xy=f(xy) # �i��������J��Ԃ�
i=i+1
if(print) cat(i,':',xy,'\n') # �݊w�N�� : c(�w�N,�i������)
}
c(i,xy)
}
sim(T)
k=1e6
RE=replicate(k,sim())
RE=t(RE)
colnames(RE)=c('�݊w�N��','�ŏI�w�N','���N=2')
head(RE)
mean(RE[,2]==7) # ���Ɗm��
mean(tu(RE[RE[,2]==7,1])) # ���Ƃ܂ł̊w��
mean(RE[,3]==2) # �ފw�m��
mean(tu(RE[RE[,3]==2,1])) # �ފw�܂ł̊w��
mean(RE[RE[,3]==2,1]) # �ފw�ƂȂ�w�N
>>557
���������ϑz���Ȃ���Z���Y������̂͂ǂ��ł���������A
�������ƃZ���Y�����ɓ����Ă݂��B
�t�F���Ǝ�R�L���`���R�ƈ��ɕς������ɂ����珬�w���ɂł��o�����肾���B
�Z���Y�����߂��Ŕn���ɂȂ����̂��H����A�ŏ�����m�b�x�ꂾ������Ȃ��B ����H�������̂����H�D�z���ɐZ��Ȃ��炢������SEX����Ƃ���ɋ�������� w���x�͋������Ȃ������Ă݂�I�n�n�n�n
>>562
���������ϑz���Ȃ���Z���Y������̂͂ǂ��ł���������A
�������ƃZ���Y�����ɓ����Ă݁B �h��ӃV���c�ゾ�Ƃ��������̂��ł��Ȃ��̂͗������w������d�����Ȃ����Z���Y�����ɓ����o���Ȃ��̂̓Z���Y�����߂��œ���������Ă��邩�炶��˂��́H
���̃X���̃h��ӃV���c�ぁ�Z���Y����]��
����ɓ����ăZ���Y����]��ł��_���I�v�l���ł��邱�Ƃ������Ă݁I
A����H��8�l�͂��ꂼ�ꐳ���҂��R���ł���A�N�������҂��R�����͂��݂��ɒm���Ă���B
A,B,C,D,E�͉R���Ȃ�K���R�������AF,G,H�͉R���ł����������Ƃ������ꍇ������B
���̏،�����m���ɐ����҂ƒf��ł�����̂�S�ċ�����B
A�u8�l�̒��ɁA�����҂�3�l����v
B�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�����҂�����v
C�uB�͉R���ł���v
D�uC��F���R���ł���v
E�u8�l�̒��ɁA���Ȃ��Ƃ�1�l�R��������v
F�u8�l�̒��ɁA���Ȃ��Ƃ�2�l�R��������v
G�uE�͉R���ł���v
H�uA��F���R���ł���v
�ފw�ɂȂ�m���Ƃ��̊w�N�A���̏ꍇ�Ɏx�������w��̊��Ғl�����߂�B
�v�Z���Ă݂����A�h��ӃV���c���̗��N�r�W�l�X���Ăڂ��������艿�i���Ȃ��B
���{�́A�u�����ɂ�����鎞��͏I������v�ƍ��ꂵ�āA���{�̃O���[�o��������𐄐i���A�C���o�E���h�𑝂₵�A�ږ��𑝂₵�A�O���l���ǂǂΓ��{�ɓ���Ċ����ǂ̊댯���������Ă����̂�����A����ɉ����Ċ����Ǒ�̗\�Z�𑝂₷�̂��B
�Ƃ��낪���{�́A�O���l�𑝂₷����ɁA�����Ǒ�̗\�Z�����炷�Ƃ����^�t�̂��Ƃ�����Ă��B
�ᔻ����ē��R�B
�����I�������w�����N�@����J�l�ł����B�ꐶ�����������ɕ��������Ƃ͂��ꂩ��̐l���ŕɂȂ邾�낤�B��t�ɂȂ邱�Ƃ͊ȒP����Ȃ���ˁB
>>567
����A�Z���Y�������������Ȃ��m�b�x��ł��Ȃ��B
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
��R�L�����Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@�Z���Y�����D���Ȃ̂��H
�J���t�@�ɂ��������Ȃ������V���c�����Q�����ĂȂ��̂��H ���{�����p���N�B�V���R��`���O���[�o�������������͍����v�z�B
���Ƃ̊��⒲�������A���ƈӎ��𔖂߂����A���ЁA�������Ȃ����A���R�Ȑl�A���A���̈ړ����������A�n���s����ڎw���A���Ȃ�B���{�������{�j��̐��i�ҁB
���̎d���͂����Ɛ��_�Ȃɒʉ@���ĂȂ�ׂ��l�l�ɖ��f�������Ȃ����Ƃ���w
>564�͓�����낤����
�Z���Y�����܂��ł���́H
�m�b�x��Ȃ̂ɁH��w���ꂽ�́H
����`��t�ɂȂ�Ȃ������i�݂͂������ˁB��҂͖������ȁB���_�Ȃ̎厡��������낤�ȁ`�����f�Â���̂�
�����͌����_��͂����Ɠ��������ق��������ȁB���O���������ɐ��_�I�ɕϒ�������Ǝv����B���Â�������҂��B���_�Ȃ̐搶�������f�@����̌����낤�ȁ`
�����͕a��������̂��낤���H����w���ō����̎��ł��Ȃ���ȂȁB�܁[��ËƖ��͖������ȁB���킢������
�����悭��w���w�ł����ȁB��҂̓K���͂Ȃ��B���_�Ȃ̎��Â����Ȃ��ƂȁB�C�̓ł����ȁB
�����ɑ��l�肵�Ă���ǃA�z���I�}�G����B
�܂��ɍ������݂̓��]���ȁB
�����܂ŃA�z������A���c�����}����H
�t�F�����̓������Ȃ��́H
�N���ɕ����Ă��������B
���͂��h��ӓ��]���炯�Ȃ̂��H
>>577
�Z���Y�����������Ȃ����Ēm�b�x�ꂶ��Ȃ��́H >>576
�h��ӃV���c��呲�͒m�b�x��Ƃ݂Ȃ���Ēp���������Ƃ����a�������邩���m�F���Ă݂܂��傤�B
���A�ǂ����H �h��ӃV���c���̑��@��
�h��ӃV���c��傪�����̂ł͂Ȃ��A�{�l�̓��������B
(p=1-c(10,16,34,9,10,26)/125)
q=1-p # ���N�m��
(P=prod(1-q^2)) # ���Ƃł���m�� ��( 1 - 2�N�A�����N�m��)
(Q=1-P) # �ފw�ƂȂ�m��
p1=p # �e�w�N��1�N�Ői������m��
p2=p*(1-p) # �e�w�N��2�N�Ői������m��
P12=rbind(p1,p2)
gr=expand.grid(1:2,1:2,1:2,1:2,1:2,1:2) #�@6�w�N�̑g�ݍ��킹data.frame
years=apply(gr,1,sum) # �e�g�����ł̍݊w�N��
dat=cbind(gr,years)
dat=as.matrix(dat) # data.frame���s��
f <- function(x){ # 1~6�N���̐i���ɂ��������N���̔z���炻�̊m����Ԃ�
ps=1 # �i�w�m��
for(i in 1:6){ # �e�g�����ł̒ʎZ�m�����Z�o
ps=ps*P12[x[i],i]
}
return(ps) # ���Ɗm��(���w���Ă��炻�̑g�����ő��Ƃł���m��)
}
Ps=apply(dat,1,f) # �g���킹����f��K�p Probability of success
data=cbind(dat,Ps) # dat[,7]:���w���Ă���̊m���@dat[,8]:�݊w�N��
# �݊w�N���̊��Ғl
sum(data[,7]*data[,8])/sum(Ps)�@ # ���Ғl=��xi*Pi�Ń�Pi=1�łȂ��Ă͂Ȃ�Ȃ��̂�sum(Ps)�ŏ��Z
# �ފw
q=c(10,16,34,9,10,26)/125
Q=numeric(6)
Q[1]=q[1]^2 # 1�N���őފw
Q[2]=q[2]^2 *(1- Q[1]) # 2�N���őފw
for(i in 2:6){
Q[i]=q[i]^2 * (1-Q[i-1])
}
sum((1:6)*Q)/sum(Q)
���{�ō��w��̒�ӎ������ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
http://2chb.net/r/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���Ƒ��Ɛ��̍݊w�N���̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƒފw�҂̍݊w�N���̊��Ғl�����߂�B �����J�P�ň��{����������~�낹�Ȃ�������}�̔�͂�
�R���i�E�C���X�̐W�^�x���A���ɂȂ������Ȃ��B
�����l����̊ό������ɖڂ������ō����̐������댯�ɂ��炷���{�W�O����
�ʂ��o�Ă��邩��Ǝq���𒓎ԏ�ŏ����Ă��ɂ��Ă���p�`���J�X��������B
��͂�A���P�̒�ӃV���c��w�����������ᐊ�ނ���킯���B
>>585
�o�O�Ƃ������ފw���̊w�N�̊��Ғl�Ƃ��Ă͐�������
�݊w�N���̊��Ғl�̌v�Z������Ȃ��ˁB draft
a=1:2
k1=2
k2=expand.grid(a,2)
k3=expand.grid(a,a,2)
k4=expand.grid(a,a,a,2)
k5=expand.grid(a,a,a,a,2)
k6=expand.grid(a,a,a,a,a,2)
f <- function(x){
n=length(x)
Pf=1
for(i in 1:(n-1)) Pf=Pf*P12[x[i],i]
Pf*q[n]^2
}
a=1:2
ko=vector('list',6)
ko[[1]]=as.matrix(2)
kp[[2]]=as.matrix(expand.grid(a,2))
ko[[3]]=as.matrix(expand.grid(a,a,2))
ko[[4]]=as.matrix(expand.grid(a,a,a,2))
ko[[5]]=as.matrix(expand.grid(a,a,a,a,2))
ko[[6]]=as.matrix(expand.grid(a,a,a,a,a,2))
f <- function(x){
n=length(x)
if(n==1) return(q[1]^2)
Pf=1
for(i in 1:(n-1)) Pf=Pf*P12[x[i],i]
return(Pf*q[n]^2)
}
a=1:2
ko=vector('list',6)
ko[[1]]=as.matrix(2)
ko[[2]]=as.matrix(expand.grid(a,2))
ko[[3]]=as.matrix(expand.grid(a,a,2))
ko[[4]]=as.matrix(expand.grid(a,a,a,2))
ko[[5]]=as.matrix(expand.grid(a,a,a,a,2))
ko[[6]]=as.matrix(expand.grid(a,a,a,a,a,2))
f <- function(x){
n=length(x)
if(n==1) return(q[1]^2)
Pf=1
for(i in 1:(n-1)) Pf=Pf*P12[x[i],i]
return(Pf*q[n]^2)
}
�J�ƈ�X�����
381 ���̖��������� 2020/02/11(��) 01:10:04.42 ID:RsjZcCEr
>>380
���O�A�}�W�R�l������ł��X�ɒ��a������c�B
�悭��҂ɂȂꂽ�ȁB
���w�͕K�{���땨���ɂ��됶���ɂ���
����Ƃ��p�����̒鋞�����H�H ����ȑ�w 156 129 113 87.6%
���}���A���i 129 124 119 96.0%
mat=matrix(c(113,16,119,5),2,byrow=T)
mat
chisq.test(mat)
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
>>586
�l���Ȃ��珰�ɂ�����\�z�����ꂽ�̂Ńv���O���������B
# �ފw
q=c(10,16,34,9,10,26)/125
Qf=numeric(6) # ���w��ފw�m��
Qf[1]=q[1]^2 # 1�N���őފw
# Qf[2]=q[2]^2 *(1- Qf[1]) # 2�N���őފw
# Qf[3]=q[3]^2 *(1- Qf[2]) # 3�N���őފw
for(i in 2:6){
Qf[i]=q[i]^2 * (1-Qf[i-1])
}
sum((1:6)*Qf/sum(Qf)) # �ފw���̊w�N�̊��Ғl
ko=vector('list',6) # kicked out �ފw�܂ł̋O��
a=1:2�@ # 1:�P��Ői��,2:�P�N���ė��N�i��
ko[[1]]=as.matrix(2) # �P�N���őފw
ko[[2]]=as.matrix(expand.grid(a,2)) # �Q�N���őފw�̋O��
ko[[3]]=as.matrix(expand.grid(a,a,2)) # 3�N���őފw�̋O��
ko[[4]]=as.matrix(expand.grid(a,a,a,2))
ko[[5]]=as.matrix(expand.grid(a,a,a,a,2))
ko[[6]]=as.matrix(expand.grid(a,a,a,a,a,2))
f <- function(x){ # �O�^���Ă��̊m���i���w����̊m���Ȃ̂ő��a���ފw�m��Q�ɓ�����)
n=length(x)
if(n==1) return(q[1]^2)
Pf=1
for(i in 1:(n-1)) Pf=Pf*P12[x[i],i]
return(Pf*q[n]^2)
}
Ef=numeric(6) # i�N���ފw���鎞�̍݊w�N�����Ғl(Q�ŏ��Z���K�v)
for(i in 1:6){
pf=apply(ko[[i]],1,f) # i�N���őފw����ꍇ�̋O�Ղł̊m��
nf=apply(ko[[i]],1,sum) # ���̋O�Ղł̍݊w�N��
Ef[i]=sum(pf*nf)
}
sum(Ef)/Q ���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���Ƃł���m���@�F�@4750970704397512 / 5551115123125783�@= 0.85585879575891107187420816324627437826646454687092053
�ފw�̊m���@�@�@�F�@ 1298308547417805 / 9007199254740992 = 0.14414120424108889384484655238338746130466461181640625
���Ƃł���m���@�F�@4750970704397512 / 5551115123125783�@= 0.85585879575891107187420816324627437826646454687092053
�ފw�̊m���@�@�@�F�@800144418728271 / 5551115123125783 = 0.144141204241088928125791836753725621733535453129079468759
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
���كV���c���كV���c���كV���c���كV���c����
��҂ɂȂ�Ȃ��������݂𑼐l�̂����ɂ���l�B���m�ł��ȁ`w
90%�ȏオ���i���鎎���ɕs���i�ƂȂ�قǂ̔ߎS�ȂقǂɒႢ���]�ŃJ�b�R�����ł��B���_�Ȃ̐搶�B�͐S�̒��ł͏��Ă��邱�Ƃł��傤�B
�ʼn��ʂő��Ƃ��A�A�A�����N���̂����ɂ������Ȃ��ˁB�S��͂킩��܂�w
���J�Ȃ���w�j�������ă_�C�������h�v�����Z�X���ɏ�����l���e�s���{���̌������ł���@�ւɏW�Ă�B�ł�����ɂ����E������̂ŐV���������̐��̍\�z�Ɏ��Ԃ�������
�����A�����߂̖��͌������a���̊m�ۂ��B
���͊��Ɉ����A�����̔��ǎw���Ë@�ւɃ_�C�������h�v�����Z�X���̋^���Ǘ�҂̎���̑Őf���������B�����炭�S��Ë@�֒f�����Ǝv����
�����ĉA�����Ȃ�����
���ꂭ�炢�s���ł��x�b�h���N�����n�߂Ă��āA����͎���1�����ɂ͕����̈�ÊW�҂����̔ł��w�E���Ă���
���͑މ@�ɂ��Ă��Ǐ������̂�48���Ԉȏ�o�߂��āA���C������̏W�����ǍD�Ȍ��̂�PCR�ɂ����A�A���Ɣ��肳��Ă���12���Ԉȏ�o�߂����̂��ēxPCR�ɂ����ĉA���Ɣ��肳��Ȃ���Ȃ�Ȃ�
�����͂������r�E�C���X���Ԃ����������킩���Ă����邱�̃E�C���X�ɂ��̑�͌����I����Ȃ�
����Ԋ뜜�����̂̓x�b�h�����܂��Čy�Ǘ���މ@�������Ȃ��܂s���Ŕ��������d�Ǘ��������Ȃ��Ȃ鎖�A�S�z�����l���a�@�O���ɎE���������������̉����ɂȂ��Ċ����g�傷�鎖
���������Ĉ�Î������s���Ă��܂��ƕ����ɂȂ�B�����ǂ̊��S�ȕ��E�͒��߁A�����I�ȃ��\�[�X�̐U�蕪���ŏ��Ղ�}���邱�Ƃ��l���Ȃ��Ă͂Ȃ�Ȃ�
�V�^�R���i�Ƃ̐킢�ő厖�Ȃ̂͂����炭����͖����͖h�����l�ނ��t�������Ă����Ȃ���Ȃ�Ȃ��a�C�ł��邱�ƁB����ɓ����ւ��ĊF�Ŏ���čs���Ȃ��Ă͂Ȃ�Ȃ�
��͂�A
���A�ǂ����H�ɂ͓����邱�Ƃ��ł��܂���ł����ˁB
�h��ӃV���c��呲�͒m�b�x��Ƃ݂Ȃ���Ēp���������Ƃ����a�������邱�Ƃ��m�肳��܂����B
���@�����m�F����܂����B
�h��ӃV���c��̑��@��
�h��ӃV���c��呲�͒p���������āA�w�Z�����F���܌����܂���B
���܂��Ɏ�R�L���ɓ��������Ȃ��̂��A�Z���Y����]��̃I�c���ł��Ȃ��B
http://blog.nihon-syakai.net/blog/2006/10/000045.html
[�{�X�g���勳���A���h�����[�E�ׁ[�X�r�b�`��
�l�I�R���͕ێ�ł͂Ȃ��B���Ƃ��Ƃ́A�č��ł́u��탊�x�����v�ƌ����鍶�����B
�c�ق�Ƃ��̕ێ�́A���j�ɑ���ߌ��I�Ȋ��o�����B���j�̐i�����ȒP�ɐM���Ȃ��B�l�Ԃ͌��₷�����݂ŁA���̌����ǂ��h�����Ƃ������Ƃ��l����B
�܂��A���{�͐l�Ԃ̎��R��N���G���ƍl����B�������A���܃l�I�R��������Ă���̂́A�č��I���l�ς��O���ɉ������邱�Ƃ��B
����͉ߌ��v�z�ł���A���[�g�s�A�v�z���B�ێ�ł͂Ȃ��A�������B�c ���a�̍G�r��́A�ێ�{���ō��ۊ��o�����������A
�啽�����^�}�̌�����6���A
��}�̌�����4���𐭎�����ɔ��f���čs�������`�����������ǁA
���͈��{�ƍق�
���{���I���͗��p10���A���Ă͎����}���嗬�h���������{�h����
���a��V���œ��{�̖����`����A�߂����k���N�̓ƍٍ��Ɖ��B
���A���͕��䌧�z�O�s�Z�����ݏZ�Œ����w��w���Ō�w�ȏo�g�̐��_�a�@�ɋΖ�����j���Ō�t�ł��B�����͖����ł��B���҂͖{���ɂ������ł���B���҂̑��������̂͂Ђǂ����܂��B
>>614
�������Ȃ��R�L���ɓ������鍑�����̈�t������͂��A����ɕ����Ă������o���Ȃ�����h��ӃV���c��Ɗm�肵�Ă���B ���_�a���҂ɑ��肷�邱�Ƃ͎d���Ȃ̂Œv�����Ȃ����@�v���C�x�[�g�ł͉����������ł��B��w����̗F�l�B���������Ƃ������܂��B���ɎႢ�����Ō�t�͐��_�Ȃ����͌�����[�L���C��[�����Ă��B
���_�Ō�̊�{�͐��_�a���҂��ςȂ��Ƃ�b������ؗ�ɃX���[���邱�Ƃł��B���܁[�Ɋ��҂���w�I�ȃg���`���J���Ȃ��Ƃ�b���n�߂邱�Ƃ�����܂����قƂ�Ǖ����Ă���܂���B���҂̂��߂ɂ����̂ق����ǂ��̂ł��B
>>617
�h��ӃV���c��呲�͒m�b�x��Ƃ݂Ȃ���Ēp���������Ƃ����a�������邩���ēx�A�m�F���Ă݂܂��傤�B
���A�ǂ����H >>617
��R�L���̓��܂����H
����ς�Z���Y����]�H�H ���ƃ}�W�Ők�Ђ̎�����}�ł悩������
�����Ɂ[�Ƃ������Ă��h�앞�������邾���}�V
�������Ɏ����}�N�\������
�����ō�������Ȃ���A���_�l���o���̂ɂ͋�J�����B
���������r���[�Ȓl������v�Z�@���Ȃ��Ɩʓ|�Ȃ̂Ő��w�ł������͔̂ɒ���t���Ă��铌�呲�̏�A�����������B
���{�ō��w��̒�ӎ������ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
http://2chb.net/r/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���Ƒ��Ɛ��̍݊w�N���̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƒފw�҂̍݊w�N���̊��Ғl�����߂�B >>616
�Ⴂ�����Ō�t�i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F���̂ǂ��炩�����Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H >>621
�n���I�ɏꍇ�����ł��铪�]��������A���Ƃ͌v�Z���B >>616
>��w����̗F�l�B��
�Z���Y����]��Ȃ̂��H
��R�L���̓��������Ă��炦�Ȃ��́H
���̑�w���Ăǂ��H
�h��ӃV���c��傶��Ȃ��́H ���{�ō��w��̒�ӎ������ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
http://2chb.net/r/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
���Z����@�����w�N�œ�N����Ƒފw�Ƃ������[���͌���������A
�����P�p���āA�Œ��P�Q�N�܂ł͍݊w�\�Ƃ��ׂ����Ƃ������Ȃ��ꂽ�Ƃ���
���̒��̗p�����ꍇ�A
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���Ƒ��Ɛ��̍݊w�N���̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƒފw�҂̍݊w�N���̊��Ғl�����߂�B ��w���Ɍ��炸�A���ꂪ�����̈ӌ����ȁB
821 ���������P���N sage 2020/02/12(��) 16:17:50.28 ID:D6l/nb000
>>813
����Ȕ�펖�ԂɃ����^w
�܂����{�͕��a����
�Ƃ肠�����ւ�Ă����ȑ�w�o�̎͂������߂Ă��� �����c�z�{�̒��N�������[�c���
���{�u���u�H�h�앞�Ȃ���ґ�I�K�t���[�^�[�Ɏg���̂ă}�X�N�Ǝ�܂����Ă�点��Ⴈ���I�v
i.imgur.com/2ZWA6Aj.jpg
���E�Ɋg�U
>>149
�S�����ӂ���B
�ǒ��l�͌����̑�����b�����d�ɏ�荞��Łi�I�j
���@�K�I�u���疽�߁v���o�����B
�����̏펯�ōl����A���S�ȃL�Z�Z�C���B
����ɃL�Z�Z�C�Ȃ��ƂɁA�ǒ��l�͂���ȑO�ɁA
�����f�������邩��������Ȃ�1F�ɁA����w���œ��U���Ă���B
��m�b�ōl����A���S�ȃL�Z�Z�C�B
�������̃L�Z�Z�C���A���ʓI�ɓ��{���~���Ă��ꂽ�B
������b���炪���悵�āA�^����ɓ��U���Ă����A
���d���A���q�����A�x�@���A���h���A�݂�ȓ��U�����ȁB
�������ɂ͂����Ȃ��B
�t�ɁA�ǒ��l�̋��C���Ȃ���A1F����͂��낼��Ƃ݂Ȃ������o���Ă����B
���̊��@�́A�}�̊_�����z���āA�ǒ��l�Ǝ}����A�h�o�C�U�[�Ƃ��ď��ق��ׂ����Ǝv����B >>22
�@�u���{����邽�߂ɂ́A�ꕔ�̐l�����ʂ��ƂɂȂ��Ă��d���Ȃ��v
�@�Ƃ����o��𐘂����̂́A�����l�����������B���������ӂ��Ɂu���̋]���v���l���āA�S�ӔC�������ŕ����o�傪�������̂́A�����������B
�@������A�����ł́A�̌��f����ɕK�v�������B���d�����ɔC���邱�Ƃ͂ł��Ȃ������B
�@�Ȃ��Ȃ�A���d�ɂ́A���f�ł��Ȃ��I���������Ȃ��������炾�B
�@ �E ��ƈ������Ȃ��Ă��d���Ȃ�
�@ �E ��ƈ�����邪�A���{�̔j�ł�����
�@���̂ǂ�����I���ł��Ȃ��B���@�I�ɁA�Ƃ����̂Ȃ�A�O�҂͈�@�Ȃ̂ŁA��҂���邵���Ȃ��B
�@�����炱���ł́A�̌��f�́A�ǂ����Ă��K�v�������B�����Đ����l�́A�Ƃ��āA�Ȃ��ׂ����Ƃ��Ȃ����B
�@���ꂪ�{�����낤�B �����l�͐���������
����ώi�ߊ��͍őO�����@���Ȃ��Ƃ�
�����l�͌����̑�����b�����d�ɏ�荞��Łi�I�j
���@�K�I�u���疽�߁v���o�����B
�����̏펯�ōl����A���S�ȃL�Z�Z�C���B
����ɃL�Z�Z�C�Ȃ��ƂɁA�����l�͂���ȑO�ɁA
�����f�������邩��������Ȃ�1F�ɁA����w���œ��U���Ă���B
��m�b�ōl����A���S�ȃL�Z�Z�C�B
�������̃L�Z�Z�C���A���ʓI�ɓ��{���~���Ă��ꂽ�B
������b���炪���悵�āA�^����ɓ��U���Ă����A
���d���A���q�����A�x�@���A���h���A�݂�ȓ��U�����ȁB
�������ɂ͂����Ȃ��B
�t�ɁA�����l�̋��C���Ȃ���A1F����͂��낼��Ƃ݂Ȃ������o���Ă����B
�w���Ȃ������邱�Ƃ̂قƂ�ǂ͖��Ӗ��ł��邪�A����ł����Ȃ��Ă͂Ȃ�Ȃ��B�����������Ƃ�����̂́A���E��ς��邽�߂ł͂Ȃ��A���E�ɂ���Ď������ς����Ȃ��悤�ɂ��邽�߂ł���B�x
���܂��͂܂��͎����̏������l���Ȃ����B�Љ�̂��Ƃ��l���闧��ɂ͂Ȃ��ł���B�n�n�n�n
���܂��̎d���́@���_�a�@�Ł@���Â��Ă��炤���Ƃ��ȁB�l�l�ɖ��f�����Ȃ��悤�ɉ߂����Ă���@�n�n�n�n
>>635
��R�L���̓��܂����H
����ς�Z���Y����]�H�H ����������Ă�o�C�g���3���^���͏��w�Z�̑��Ǝ��ŊŌ�t���z�u�ł��Ȃ��̂œ����������͓���Ȃ��ƌ���ꂽ�B
�ł��A����������A�L���x�Ɉ������ċ��^�͕⏞���܂��Ƃ̂��ƁB
��͂�A�h��ӃV���c�ザ��Ȃ�����厖�ɂ���Ă���Ȃ��B
>>635
�h��ӃV���c���ɓ��w���邱�Ƃ�I�������I�}�G�́A�A�ꐶ�A�����n���Ɣl���邱�Ƃ����Ă����̂��H ��Гo�^�̏���������ƁA�ǂ��̈�w���𑲋Ƃ��Ĉ�t�Ƌ����l���������������悤�ɂȂ��Ă����Ȃ��B
�h��ӃV���c��呲���ƍ�����w��w���ɍē��w���Ă���t�Ƌ��̓h��ӃV���c��呲�Ŏ擾�̋L�^���c���B
�s���̖����e
>>
���͏��a�̎���ɑ�w�������ǁA�͍̂��������ʊ��������A���ꖯ�̂��߂̓���w�Z�Ƃ����C���[�W�ŊJ�ƈ�̃o�J���q�ȊO�͒N�����悤�Ƃ��炵�Ȃ������B
�펯�I�ɍl���āA���疜�Ƃ����@�O�ȋ����āA���������Ǝ҂�������҂�����o�J���̗������̂ƎU�X�l����̂��킩���čD���D��Ńh��ӈ�ɍs���������͈�l�����܂���ł����B
�{�l�ɂ͖ʂƌ������Ă͌���Ȃ�����ǁA�����炢�̔N��̐l�Ԃ́A�����炭�͂W�|�X���̓h��ӈ㑲�����ł��u���̂����Ȃ��Ɣ������Ă�A���̗����o�J���v�ƐS�̒�Ōy�̂��A�}���Ă����B
���̖{�l�ɂ͖ʂƌ������Ă͐�ɂ���Ȃ��Ƃ͌���Ȃ����ǂˁB
<<
�������̎����͗������w�����ݐi�s�`�ł��邱�Ɣ@���ɂ��߂�����������ˁB
�V���c��̎g���͗������w�o�ō����^���̐擪�ɗ����Ƃ���B
�������w�̊w�������Џ����ɂ��Ȃ�������A�M���̉͂Ȃ��ˁB�܂�A���܂Ōo���Ă��V���c��呲�������o�J�Ɖ����͐@���Ȃ��B�V���c�o�g�҂����A�������w�Ɍ��������������i����ׂ��B
�������w��t�̖Ƌ����D���I�̍����^���̐擪�ɗ��Ă悢���B
�l���������w�Ƃ��A�����Ă���M���̉͂Ȃ��B
���䌧�z�O�s�Z�����@�n�n�n�n
���̌f���@�݂��������H�n�n�n�n
>>642
>>617
�h��ӃV���c��呲�͒m�b�x��Ƃ݂Ȃ���Ēp���������Ƃ����a�������邩���ēx�A�m�F���Ă݂܂��傤�B
���A�ǂ����H ����������Ă�o�C�g���3���^���͏��w�Z�̑��Ǝ��ŊŌ�t���z�u�ł��Ȃ��̂œ����������͓���Ȃ��ƌ���ꂽ�B
�ł��A����������A�L���x�Ɉ������ċ��^�͕⏞���܂��Ƃ̂��ƁB
��͂�A�h��ӃV���c�ザ��Ȃ�����厖�ɂ���Ă���Ȃ��B
���_�Ȃ̐搶�����炷�Ȃ�B�A�n�n�n�n�n�n�n�n�@�ł�@�f���݂��������H�q�q�q�q
���䌧�z�O�s�Z�����@�����̌f���Ł@�����Ɗ撣���I�q�q�q�q
�u���{�T�|�[�^�[�Y�v
�����@�@�����ň��{�W�O�s���`�@���@��}�́A�����厖�ȃR���i������I
���݁@�@���ق̊����͂��o���A�Ƃ��Ƃ����҂��o�����Ԃɔ��W�A�����Ή��ɔ��W���@���@�R���i�R���i���đ��������Ȃ�I
���{�T�|�[�^�[�Y�u���{�W�O�t����@���z�͔��A�R���i�Ή��ɍ����̎x���͍����v
���ʂ̓��{�l�u���H�@���͊����g�債�Ă��āA�Ƃ��Ƃ����҂܂ŏo����ł���H�@���{�l�̖����댯�ɎN����Ă��ł���H�{�鎖���������҂ł���H�v
���{�T�|�[�^�[�Y�u���O��A�K���Ɉ��{�K�[�A���{�K�\�A�ő��v
���ʂ̓��{�l�u���O��A���������ǂ��̍��ЂȂ�E�E�E�v
���{�T�|�[�^�[�Y�u��}�K�\�A��}�K�\�A��}�K�\�E�E�E�v
���ʂ̓��{�l�u�}�W�Ō����Ă�̂��H�A�l�^����Ȃ������̂���A�A���܂���E�E�E�v
>>646
�h��ӃV���c��呲�͒m�b�x��Ƃ݂Ȃ���Ēp���������Ƃ����a�������邩���ēx�A�m�F���Ă݂܂��傤�B
���A�ǂ����H ���f�B�N���f�B�A�Ńo�C�g���Ă��ˁB���܂�̔�펯�œr���Œǂ��o���ꂽ���ǂȁB���n�n�n�n
>>650
���܂ő��l�̘b�������Ă�B
��R�L���͉������̂��H�Z���Y����]����H
���A�ǂ����H >>652
12�N�����ł�462�ʂ�
��v�Z�������Ă���B �w������́@�ǂ����̉��h�ɂ�����ˁ@�����ā@�}�}�`�����Œʊw���Ă��ˁI
���n�n�n�n
�f��������Ƃ����ˁ@���[�n�n�n�n�@�����悶���قǏ��Ă��܂��@�ӂӂӂ�
>>654
����A���}�n�̃o�C�N�Œʊw�������B >>654
>>650
���܂ő��l�̘b�������Ă�B
��R�L���͉������̂��H�Z���Y����]����H
���A�ǂ����H p=1-c(10,16,34,9,10,26)/125 # �i���m��
q=1-p # ���N�m��
p6=prod(p) # 6�N�ő��Ɗm��
f <- function(x) prod(q[x])
pf=c(6,p6) # �݊w�N��,���̊m��
for(i in 7:12){
cmb=gtools::combinations(6,i-6,rep=T)
pf=rbind(pf,c(i,p6*sum(apply(cmb,1,f))))
}
(P=sum(pf[,2]))# 12�N�ȓ��ɑ��Ƃł���m��
sum(pf[,1]*pf[,2])/P # ���Ƃ܂ł̕��ύ݊w�N��
>>657
2���ފw�̔�������Ɗm���������ቺ����Ȃ��B �r�f�I���ł̃o�C�g�B�G���r�f�I�����Ŋӏ܂ł��Ă悩�����ˁB�A�[�n�n�n�n
���̘A���������ȁB�r���S������ȁB
>>659
���܂ő��l�̘b�������Ă�B
��R�L���͉������̂��H�Z���Y����]����H
���A�ǂ����H ���@����������܂����B
�h��ӃV���c��呲�͒p���������āA�w�Z�����F���܌����܂���B
>>659
>���̘A���������ȁB
���������Ƃ����Ȃ��R�L���̓��������Ă��炦��̂��H
������������V���c��Ȃ̂��H�Z���Y����]�Ȃ̂��H ���{�����Ƀo�C�I�e��������Ɛl�̔ƍs����������ȁB
���{�Ŋ���Ă���؋��E�ؐl�̊F�l�A�ނ��2020�N�̏t�߂̌䈥�A��\���グ�܂��B
���t�A���̍炭���ɁA�K�ߕ����Ǝ�Ȃ����o�Ƃ��ĖK�������\��ł��B
�t�߂ɍۂ��āA�����Ă܂��A�I�����s�b�N�E�p�������s�b�N���̋@���ʂ��āA�X�ɑ����̒����̊F�l���K������邱�Ƃ��y���݂ɂ��Ă��܂��B
���̍ہA���Г����ȊO�̏ꏊ�ɂ������^�сA���̓y�n�Ȃ�ł͂̓��{�炵���������Ē�����K���ł��B
2020�N1��
���t������b
���{�W�O
�D�G�Ȗ�}�̖������Ė{���ɐ����S���\�͂Ȃ̂��낤���H
���t������b���`�F�b�N����A�@�\�̂ق����厖���Ǝv����
���ꂪ�܂Ƃ��ȎO���������B
���������̖����A�̎����𑁁X�ɒ�o��
���@�{�ɂ����߂�����̂͋M���A���{����
����������܂ō��������Ă��錳�����Ƃ���
���o����Ȃ��I�{�b�`�}��
://i.imgur.com/QfHDabz.jpg
����20�q�����̎��@���I���ē쑊�n�s�̑��o�ی����ŃX�N���[�j���O��������}�슯�[�����B�悭�o����Ă�1�l�����t���A�[�}�[�̉摜�͂��̎���1�R�}����������́B
������20�q�����ɓ������҂̓X�N���[�j���O��������悤�Ɏw��������Ă��āA20km���̂����O���ɂ��鑊�o�ی����ł��X�N���[�j���O�������s���Ă����B
://i.imgur.com/GtX7lnE.jpg
://i.imgur.com/VVjDiAt.jpg
�ʂ̊p�x����B�����摜�ɂ͎}�슯�[�����Ɠ����i�D�̎��@�ɓ��s���Ă����҂���������B
://i.imgur.com/P8QubkQ.jpg
�X�N���[�j���O�������I���ē����ꏊ�ŕ��ʂ̍�ƒ��ɒ��ւ��Ď�ނɉ�����}�슯�[�����B
://i.imgur.com/fEDjDGT.jpg
���������{����20�q�����̎��@�̗l�q�B�E�����l�ڂ��}�슯�[�����B
���@��̍s���s���҂̑{�������}�슯�[�����Ɠ����i�D�����Ă���B
>>668
CONCLUSIONS AND RELEVANCE In this single-center case series of 138 hospitalized patients
with confirmed NCIP in Wuhan, China, presumed hospital-related transmission of 2019-nCoV
was suspected in 41% of patients, 26% of patients received ICU care, and mortality was 4.3%
ICU36�l�@����6�l�Ȃ̂ŏd�lj�����ƒv������16.7% (95%�M����Ԃ�6.4%-32.8%) ���܂��͂܂��͎����̏������l���Ȃ����B�Љ�̂��Ƃ��l���闧��ɂ͂Ȃ��ł���B�n�n�n�n
>>672
>���̘A���������ȁB
��R�L���ɓ��������Ȃ������̂��B
������������V���c��Ȃ̂��H�Z���Y����]�Ȃ̂��H >>671
�v������1/6���x������d�ǗႵ�����Â���Ă��Ȃ����Ă��Ƃ��H ���܂��͂܂��͂��ꂩ�玩�����ǂ��������Ă��������l���Ȃ����B���܂��̗���ł́A�Љ���͍l���Ȃ��Ă�������B���n�n�n�n
>>675
��R�L���̓��܂��H
���k�ł���l���Ȃ��́H
�݂�ȃh��ӃV���c��Ȃ̂��H ���܂��̎d���͂����Ɛ��_�Ȃɒʉ@���邱�Ƃ���@�厡������点��Ȃ�I
���_��Q�Ҏ蒠�Ő����ł��邩�ȁ@���n�n�n�n
>>678
�Ⴂ�������C�ォ��܂���R�L���t�F�������Ă�����ĂȂ��́H
�Z���Y����]��H�N���ɑ��k���ē����o���Ă��������B
������������炯�Ȃ珕�����������낤���ǁB
�Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F���̂ǂ��炩�����Ă�����A�����łȂ���������Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H >>679
���͒m�b�x��̎蒠�������Ă�Ȃ��́H
�Z���Y�����������������Ǝx������Ȃ��̂��Ȃ��B >>685
���炩�Ȕƍ߁i���_�ʑ��j������A�T������IP�A�h���X���J�����ăv���o�C�_�[�����O���J�����邾�낤�ˁB >>669
�@���������������Ȃ��B
�i�`�l�`�̍ŐV���@free access�œǂ߂�
Clinical Characteristics of 138 Hospitalized Patients With 2019 Novel Coronavirus?Infected Pneumonia in Wuhan, China
https://jamanetwork.com/journals/jama/fullarticle/2761044
CONCLUSIONS AND RELEVANCE In this single-center case series of 138 hospitalized patients
with confirmed NCIP in Wuhan, China, presumed hospital-related transmission of 2019-nCoV
was suspected in 41% of patients, 26% of patients received ICU care, and mortality was 4.3% �K�ߕ����o���ق�ό������i���̋�����j�̕��j�����{���o���Ă��邩��A�h�u�����������Ă��p������Ă����낤�B
���Y�}�����N��4���ɃC���o�E���h���i�Ŗ��m�̊����ǂ��������܂�郊�X�N�����̏�\�����邩�̂悤�ɐ������w�E���Ă���B
�����̑S�d���r���͂��蓾�Ȃ��Ƃ����_�b�𐭕{�̌��������ɂ��Č��������g�_�E�������������J��Ԃ��Ă����B
��@�ɑ���ʍ\���̂��̈Ⴂ


���ꂾ���ň�ڗđR���낤 �V�c�a�����̈�ʎQ��𒆎~������肩�H

�O���[�o���Љ�̖��̉��Ɋ�Ƃ��O���[�o��������
�����������Nj��͎����ł̌ٗp��Y�\�͂�D��
����̂悤�ȕs���̎��Ԃɂ����Ă��Ȃ�̎Y�ƂŎ��͍������ɂȂ��Ă����������܂��܂��ƌ��������Ă�
�B���Ă��̂͝\�߉f����
����Ȃ̌��J����K�v�͂Ȃ���
�x�@�ł��ߕ߉f���������������J����̂��H
sengoku38�H�@�����A���ꋳ����{��c�̈�F����ł��������H
�l�g�T�|�A���O�炳�[
�����S�y����̓������~�߂��A�h�앞���p�̋`����������
�K�ߕ������o�ҋ��ŏ��҂��āA���a�������̒����ɂ͑�K�͎x������
��}�̌��J�ψ���J�×v�����f�葱���āA���a�w����x���
�����g�債�܂����āA�]���҂��o�Ă�̂�
�����l�g�T�|�͖�}�K�[�A��}�K�[w
�z���g������̓N�Y����
���R�́A�����Ȃ�킢�i����ő��ł͋c�_�����Ȃ��j�A���E�Ɛ킢�i�ږ��ɂ̓m�[�^�b�`�j�A�A�����J�Ɛ�����i�N�����v�v�]���̔p�~�j�A���{�l�ɂ͂��������Ȃ��ɑ���������B
���{�́A�����ȂɛZ�сA���E�ɛZ�сA�A�����J�ɛZ�тĒ����������ێ����Ă��������B
�c�O�Ȃ���A���{�l�ɂ͈��{�̂悤�ȈË������������B
�_�C�v�����d�Ǐo�Ăē��{�l�܂܂�Ă钆
�N���[�Ƌq�ŗ�܂������Ă��Ē���
��c�̕������ƓS�Ă��f�[�g���āA���g�b�v�̋����Ղ肶��ˁH
�܂��Ŗ�������Ă��������B�ɍ������̂Ăē������݂̑����ȁ[���Ďv����K�`��
���ق�x�@�̐l�����Y�^�{���ɂ��Ă��܂�����
�������Ǘ��̂������������
���{�̖������@�̂����ʼn��l�̖�l���a��Ŏ��E�ɒǂ����܂ꂽ��
��������������܂����ċ����j��
�J�W�m���I�����s�b�N������������
���܂ŔN���������~��������ɓ˂����̂�
�h�[�s���O����߂��u�ԂɌo�ς���_���[�W����
311�̂Ƃ�����͖��ɐ^����������������ĕs���s�x�Ő���Ă���
�����͖�肪�N����ƊW�����ĉ����������Ƃɂ��Ă�悤�ɂ��������Ȃ�
����A�����֔z������ƌ����z��̍s�����ُ킾��ȁB
�����������Ȃ���A�����p�̔��~�����シ���A�u�a��Q���⏬�����悤�Ƃ����B
�������r�����Ȃ��ƃ}�g���ȓ������W�Q����ă��`���N�`���ɂȂ�B
����̂��ƂōĔF��������B
���{���{�́A�t�߂ő�ʂɃE�C���X�𗬓������Ă��܂��������̑厸�s���B�����Ȃ��Ă͂Ȃ�Ȃ��̂ł�
���̂��߂ɓ��{���̕a�@�Ɍ��������邱�Ƃ��֎~�����̂ł�
�݂Ȃ���������Ȃ��̂́A�ЂƂ��ɐ����̉B���H����A�����邽�߂ł�
�����̂ĂĐ��������܂��傤
�ق�܂�
�V�^�C���t���G���U�������ʑ[�u�@�ł��ً}���Ԑ錾�ł������
https://elaws.e-gov.go.jp/search/elawsSearch/elaws_search/lsg0500/detail?lawId=424AC0000000031#223
���i�V�^�C���t���G���U���ً}���Ԑ錾���j
����O�\����@���{���{�����́A�V�^�C���t���G���U���i�����̐����y�ь��N�ɒ������d��Ȕ�Q��^���邨���ꂪ������̂Ƃ���
�����߂Œ�߂�v���ɊY��������̂Ɍ���B�ȉ����̏͂ɂ����ē����B�j�������Ŕ������A
�����̑S���I���}���Ȃ܂ɂ�荑�������y�э����o�ςɐr��ȉe�����y�ڂ��A
�����͂��̂����ꂪ������̂Ƃ��Đ��߂Œ�߂�v���ɊY�����鎖�ԁi�ȉ��u�V�^�C���t���G���U���ً}���ԁv�Ƃ����B�j�����������ƔF�߂�Ƃ��́A
���V�^�C���t���G���U���ً}���Ԃ����������|�y�ю��Ɍf���鎖���̌����i��܍��y�ё�O�\�l���ꍀ�ɂ�����
���u�V�^�C���t���G���U���ً}���Ԑ錾�v�Ƃ����B�j�����A���тɂ��̎|�y�ѓ��Y����������ɕ�����̂Ƃ���B ����̘b�ɂ͂������ł��Ȃ�
���̂悤�Ȃ��Ƃ��N���Ȃ��悤���S�̑̐����Ƃ��Ă���
���E�ō����x���̊����Ǒ���Ƃ��Ă��邩�炻�̂悤�Ȃ��Ƃ͋N���肦�Ȃ�
�g�b�v�א��҂��ǂ�ȂɎ��I�ȕ����≘�E���̈��s���d�˂Ă��A���̊�@�ɂ͖��̖�����Ɏ��Ƃ����Œ���̋`����������Ȃ�����͎x�����ꑱ����A�A�x�͂������������ƕ��������B
�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@ �^::::::::�\::::::::::�J'�R�A
�@�@�@�@�@�@�@�@�@ /:::::::-�A:::i�Li|::|/:::::::::::�R
.�@�@�@�@�@�@�@�@ /::::::,,�A�~"�R�M�@"�J�@/ ::::::�R
�@�@�@�@�@�@�@�@/::::::==�@�@�@�@�@�@�@�@`-::::::::�R
�@�@�@�@�@�@�@�@|::::::::�^ .,,,=��,�@,��=�A�A l:::::::l
�@�@�@�@�@�@�@�@i::::::::l�J�@,�^��_,!.�^��_�A,l:::::::!
�@�@�@�@�@�@�@�@.|`:::|�@�@�@" �m/�@i�_`�@�@ |:::::i
�@�@�@�@�@�@�@�@�@i ���@�@�@,�B____.i i�@�@�@i //
�@�@�@�@�@�@�@�@�@�R i�@�@�@/�@ l�@�@.i�@�@ i /�@�@���W�O���Q�@���{�l����
�@�@�@�@�@�@�@�@�@�@l �R�@�m `'''�M'''''�L�R�A/�L
�@�Q�Q�Q�Q�Q�^|�A �R�@�@�M�P�L�@ �^�Q�Q�Q
�i���@�@�@�@�@-i�L�@ l �R�@�M "�[�|�L/�@�@�@�@�@���j
�@�P�P�P�P|�@�@/�@�@�B�@ l�@�B �@�l�@|�P�P�P
�@�@�@�@�@�@ /�@/ �R�@�[�@�@�@-�@/�@�_�_
�@�@�@�@�@ /�@/�@�@|�@�@�@�@|�@�@ |�@�@�@�_�R
�@�@�@�@ /�@/�@�@�@�R�@�@�@�@�@�@ |�@�@�@�@�@�_
�@�@�@ /�^�@�@�@ �^�@�@�@�@�@�@�@|�@�@�@�@�@�@ �_
�@�@ /�@�@�@�@�@�^�@�@�@�@�@�@�ց@�@�@�@�@�@�@�_
�@ /�@�@�@�@ �^�@�@�@�@/�ցR�@�@�@ �_�@�@�@�@�@�@ | |
../�@ �@�@ �^�@�@�@�@�^�@�@�@�_�@�@�@ �_�@�@�@�@�@|�@|
/�@�@�@�^�@�@�@ �^�@�@�@�@�@�@ �_�@�@�@�_�@�@�@ .|�@ |
|�@�@ �i�@�@�@�@���@�@�@�@�@�@�@�@�@�@�j�@�@�@�j�@�@�@|�@�@|
|�@�@�@ �_�@�@�@�_�@�@�@�@�@�@�@.�^�@�@ �^�@�@�@|�@�@�@|
�b�@�@�@�@�_�@�@ �_�Q�Q_�Q�^�@�@�^.�@�@�@�@|�@�@ /
�@|�@�Q�\�\-�_�@ �_�@�@ �^�@ �^-�\�\�Q__|�@�^
�@�@�@�@�@�@�@�@�q_�Q_�m�@�@�R�Q__�j
���R�́A�����ȂƐ킢�i����ő��ł͋c�_�����Ȃ��j�A���E�Ɛ킢�i�ږ��ɂ̓m�[�^�b�`�j�A�A�����J�Ɛ�����i�N�����v�v�]���̔p�~�j�A���{�l�ɂ͂��������Ȃ��ɑ���������B
���{�́A�����ȂɛZ�сA���E�ɛZ�сA�A�����J�ɛZ�тĒ����������ێ����Ă��������B
�c�O�Ȃ���A���{�l�ɂ͈��{�̂悤�ȈË������������B
�����l�͓��H�呲��
���q�͂͏ڂ��������͐M��������
���{�͐����呲��
�������ǂ߂Ȃ�
�����u�a�ɂȂΉ��ł����
�ܗ֒��~�͈�������Ȃ�
�ܗ֒��~��|��Ċ����Ǒx��
���̌��ʁA�吨�̐l�����ʂ��Ƃ�����������
�����d�Ԃ��A���̂�������ɔ����d�ԂɂȂ�B
�o�Ђ���ΎГ��Ŋ����t���O�B
�}�X�N�Ȃ��̂����{�̐ӔC
�]����{�ɋK���ł���
�Ƃ������V�C���t�������[�@�ŋ��o�������������
���������]���Ǝ҂Ȃ�ăN�Y���̂��̂�����d����l�ȉ��ŋ��o�����������
��p�͓]���A�A�o�֎~����
���̍��͈�́H
�ی����Љ�ėz���Ȃ����������A��f���̂���f�Ï��F�肳��Ă����Ƃ����ԂɊ��җ��Ȃ��Ȃ�B�\�͈�u�ɍL�܂�ˁB
�����̓X�e�[�L�n�E�X�̗\����L�����Z���B
�R���i�����������܂ŊO�H�͎��l�B
�t�F�����ɂ͓����o���邩�玩�l�Ȃ���
�h�Жh�u�͋��Y�}�̕����L�\�Ȃ�Ȃ����ȁB
�����̑S�d���r���Ƃ��C���o�E���h�Ŗ��m�̊����ǂ̐N����
�I�m�ɗ\�����Ă���B
�ǂ�������{���������đ�S���B
�����J�P����������͈��{���ېg���Ă��A���v�U�����Ă��炦��
�x�T�w�A���ƁA���{�F�͈��{���x���������邪�A
�R���i�͈��{���ېg�Ńf�[�^���B����˂����āA�ېg�}���
�����S�Ă̌��N�ɉe�������邩��A������Ȃ�
���{���Ă��̎����܂�ŕ������ĂȂ�
�c�z�{���N�l�ɉ������Ă����ʁB
���ׂĂ͓��{�l�r�łƗ������Č��Ɍ������Ă���B
�m��ʂ͓��{�l����Ȃ�B
�^�N�V�[������瑋���J���Ă���B
�d�Ԃɏ������N95���B
�������̎��ɔ������̂��𗧂����B
�K�C�K�[�J�E���^�[��烈�[�h�܂��������Ȃ��B
�Ƒ�����͊댯�~�������ꂽ���ǁB
�y�ߓ��x��E���q�͈ψ����z���̒���A�����ߓ����Ɏ��̂��g�債���ꍇ�̑z�������悤�˗������B�ł����̂��u������P���q�͔��d���̕s�����ԃV�i���I�̑f�`�v�B����͓��e�̂����܂��������Ɂu�ň��V�i���I�v�Ƃ���B
�g�����v�̓N���[�Y�D�Ή��ł͈��{���A�z�Ȃ̂������ɗ��p�����ȁB
�č��l�~�o���Ȃ��Ɣᔻ�����邵�A���X�œ��������Ă��ᔻ������B�܂��������̓��{�Ɉϑ����ē��{�������ł����̂ŃA�����J�����������~�o�ƁA��m���ȁB
>>721
��R�L���͌����ɒʂ����w���ł������ł���B
�������ƃ`���R�ɂ������ǁB >>722
���낵���̂����w���̓��]��������Ă��Ȃ��h��ӃV���c�ゾ��B ���ȔF���E���㎑�i�@�����{���R�K���Ώƕ\�i�C���Łj
�Q�����@�@�@���ȕW�Ԉ�Q�N����
�P�����@�@�@���ȕW�Ԉ�Q�N�ȏ�T�N����
�㓙���@�@�@���ȕW�Ԉ�T�N�ȏ�P�O�N����
�ޒ��@�@�@�@���ȕW�Ԉ�P�O�N�ȏ�
�R���@�@�@�@���F����Ȉ�
�����@�@�@�@�T�u�X�ؐ���P��
�y�с@�@�@�@�T�u�X�ؐ���Q�ȏ�
���с@�@�@�@�V���Ȑ���
���с@�@�@�@�V���Ȑ���+�T�u�X�ؐ���P��
��с@�@�@�@�V���Ȑ���{�T�u�X�ؐ���Q�ȏ�
�����@�@�@�@�������Ȑ���
�����@�@�@�@�������Ȑ���+�T�u�X�ؐ���P��
�卲�@�@�@�@�������Ȑ���+�T�u�X�ؐ���Q�ȏ�
�y���@�@�@�@�_�u���{�[�h��i�������Ȑ���+��{�̈����P�j
�����@�@�@�@�_�u���{�[�h��+�T�u�X�ؐ���Q�ȏ�
�����@�@�@�@�g���v���{�[�h��i�������Ȑ���+��{�̈����Q�j
�@�@�@�@�@�@�@+�T�u�X�ؐ���Q�ȏ�
�叫�@�@�@�@�N�A�h���v���{�[�h��i�������Ȑ���+��{�̈����R�j
�@�@�@�@�@�@�@+�T�u�X�ؐ���Q�ȏ�
�����e�^�҂̃h��ӃV���c��̒n�ʂ́H
�M���Ăق����Ȃ�M������؋����o���ςނ���
���{�̌����Ă邱�Ƃ͗e�^�҂��u�A���o�C�͎����Ȃ�������M���Ăق����v�Ǝ撲���Ɍ����Ă�̂Ɠ���
���̌��ŗe�^�𐰂炷���������Ηe�^�͐����̂ɁA��������悤�Ƃ��Ȃ��̂Ȃ�^����͓̂��R
�m�b�x����{���������ɂ��ׂ�����
�E�����l�̓n�q���������Ē����l���A��������
�E�I�����s�b�N�̒��~��錾����
�E�I�����s�b�N�{�݂������҂̊u���{�݂Ƃ��Ďg��
�E�S���ɗՎ��̊����Ґ�p�a�������
�E��T�Ԃ̊O�o�֎~�߂��o��
�E�����𖼏��o���l�Ɉꎞ�����������o��(�B����h������)
>>729
���܂��Ɏ�R�L���ɓ��������Ȃ��̂������V���c�� >>729
�Ȃ��Ȃ�
�w�͂��Ă��ʖڂȓz�͂��܂�Ƃ��� >>115
> ���{�����Y�̃o�J��
�������A�����͌c����SFC���B
�ǂ����猩�Ă��u�����g�v����B
���Ȃ݂ɁA�c���̗�����́A���̏��ɍ����B
�@�@1)�@�@�w�������w�ȁi�����Ƃ̃o�J���q�̓R�R�j
�@�@2)�@SFC�i����B90�N��ȍ~�́A�R�R���}�L�j
�@�@3)�@���w���i���E�̃o�J���q�͂����j
�@�@4)�@���w���i�����E�E�}�X�R�~�E�|�\�X�|�[�c�E���N�U�E�̃o�J���̓R�R�j
�t�ɁA��E�H�E�o�́A�����͏��Ȃ����A���Ƃ������ł����Ă��A����Ȃ�Ɏ�������
�w�͂�����悤�ɂȂ�l�����邩��A�����̓}�V�B >>732
���̃X���̃h��ӃV���c�オ��������ˁB
����������̃A�z�������R�L���̓��������Ȃ��Ɛ������Ă��A�n�������ė������������ɂ���Ȃ��̂��ȁH >>700
�~���V���K�[���烄�N�V���K�[�ɕ��j�ύX���B �D���łЂ�����E�l�E�C���X��|�{���āA���Ƃ͖�ɕ������̊ȒP�ȃe���ł�
���s�Ƃ����݂��Ȃ��̂ŁA�N���ƍs���~�߂鎖���߂܂��鎖�������A���S�����̃e������
���̖����ʎE�l�E�C���X�e����B��~�߂鎖���o����̂��R�̂Ȃ킯�����A���� ���ꂪ�����������ɂ͊��ɍ����͖ܘ_�A�S���E�ł��唼���E�C���X�ɉ�������Ă��邩��A�����̂Ƃ���ɉ���Ă���܂łɓr�����Ȃ��N����������
���̊ԂɑS�ł���
�m��w����ȁH

�Ȃ�ŗV�ѐl�̑D���Ƃ��̂��߂ɍ������댯�ɂ��炳�Ȃ���Ȃ�˂�
�D���ƒ��߂�
>>736
���{���̎�d�҂͂�����W�O��
���N�l������� �c�z�{�͖����������e�����X�g
658 ���O�F���������P���N[] ���e���F2020/02/20(��) 12:55:57.53 ID:3BjtivZl0
����������Ƃ��e���v���ɂ��Ƃ�
�y���[�j���O�V���[��c��t�̔����܂Ƃ߁z
�E���b�h�]�[���ƃO���[���]�[���������Ă�ꂨ�炸�A�{���̒��ɖh�앞�𒅑ւ���ꏊ�����������߈�ÊW�҂ɂ��������g�債���B
�E�{���͑��{����O���[���]�[���͑D�O�ɒu���āA�D���͂܂�܂郌�b�h�]�[���ɂ��ׂ��������B
�E�����Ȃ����͓̂��{��CDC(�u�a��Z���^�[)�̂悤�ȉu�a��̑g�D���Ȃ����Ƃ����B
�ECDC���풓�I�ɑD�ɓ���ӎv����Ɗe���ւ̎w�����s���A���X�����W�����āA������V���Ă������Ƃ��K�v�������B
�E���{�͂����������Ƃ��N����ƐF��ȂƂ��납��Z���ԁA���Ƃ��W�߂��ČʂɑΉ������Ă邪�A�ӎv����͊����ɂ���ĂȂ���Ă�B
�E���ƂłȂ��������v�����𗧂Ă�ƁA�O���[���]�[���ƃ��b�h�]�[���̌`�Ȃǂ͈ꉞ��邪�A�敪����^�p�ȂNJÂ��Ȃ��p���Ȃ��B
�E���{�͢��@�Ǘ��̐��Ƃ��풓���Ă�����ƌ������A�F��ȑg�D�̐F��Ȑ��Ƃ���������ւ藧������ʂɓ����Ă�̂ł͢�풓��Ƃ͌����Ȃ��B
��т����v����������`�[���Ƃ��đ��݂��Ă��Ȃ��B
�E���������ƂɈӎv����̌������Ȃ��B�ŏI�I�ɂ��ׂĊ����ɂ��f���𗧂ĂȂ��Ă͂����Ȃ��B
���ۓI�ɢ�����\�h�`�[����ƌ�������̂Ƃ͑S���Ⴄ�B
�E������̎����Ɋւ��Ă͊��S�ɐ��ƂɔC����ׂ��B�����ɐ����I�Ȏv�f�Ƃ��z���Ƃ�����ׂ��ł͂Ȃ����A�����Ȃǂ��Ȃ��悤�Ɉӎv����̃v���Z�X�͖��m�ɂ��Ȃ�������Ȃ��B
(�L��֥`)���{�x���]�[�j���O�摜�̃c�C�b�^�[�폜����w�Ղ肾��


����}����
�E�V�^�C���t���G���U�}������
�E�����u���Ȃ�Ƃ��S�����ʼn���
�E�Β������d�Ή�(��t���L��)
�E�����ɏ�荞�ށB�S����������~
�E�������̓����A�Q�Ȃ��őΉ�
���{����
�E�V�^�R���i�}���厸�s
�E�R�����P�N�T�����o���Ă����������A��ނȂ��ؔM�ɉ��̂��Ă��܂���
�E�Β����y�����O��(�t�ߑ劽�}�A�n�q�p���A�K�ߕ����o����)
�E���܂ł����������O���A�����z�e���߂���
�E�N���[�Y�D�������
�E�R���i���c�ɁA���݉�Ŋt���R�����ȁ�New!
�E�]�[�j���Ow ��New!
����̍��Ǝ����͎��ȍ̓_�ō��i���Ă�Ǝv���@1�N�Ԗҕׂ����b�オ�������@�������瓯�����̔ޏ��ƃn���C�֗��s���@�ޏ������i���C���ɓ����Ă���B�y���ނ��[
����ŐV�^�x���̘b���Ă����ɂ��������Ȃ�����
������������Ă�Ⴂ����
���{�����̔�Q�҂���
����}����
�E�V�^�C���t���G���U�}������
�E�����u���Ȃ�Ƃ��S�����ʼn���
�E�Β������d�Ή�(��t���L��)
�E�����ɏ�荞�ށB�S����������~
�E�������̓����A�Q�Ȃ��őΉ�
�E�k�ЂɕK���ɑΉ��GDP��
���{����
�E�V�^�R���i�}���厸�s
�E�R�����P�N�T�����o���Ă����������A��ނȂ��ؔM�ɉ��̂��Ă��܂���
�E�Β����y�����O��(�t�ߑ劽�}�A�n�q�p���A�K�ߕ����o����)
�E�k�Ђǂ��납�䕗��^���ł���S���Ή��ł��������I��
�E���܂ł����������O���A�����z�e���߂���
�E�N���[�Y�D�������
�E�R���i���c�ɁA���݉�Ŋt���R������
�E�]�[�j���Ow ��New!,
�E�����ǂ̐��Ƃ��o�b�V���O����������A�挊���@�� ��New!
�E�\�Z�C�������@��New!
�����̖��F�ł��郍�V�A��k���N�ł���A�����l�����֎~�Ȃ̂�
���{�͉�������Ă�낤��
���{�������l������֎~�ɂ���O��
���E������A���{�l�������֎~�ɂȂ�̂��A���Ԃ̖�肾��
> ���E������A���{�l�������֎~�ɂȂ�̂��A���Ԃ̖�肾��
���ꂪ���W�O�̖ړI����
�R���i�ŐW�O�`��������
���o������Ƃ��̓`���z������邯��
�����N�����Ƒ��X�J��
ATM�̉^����Ȃ�
�t���A�[�}�[�}��͐�������������
���{�������}�q������킯�ɂ͂�����
���ʂP�U�ƐԋʂS������B�������P�O�̔��Ɋe�X�Q������ׂɕ��z����Ƃ��A
�ԋʂQ���������������傤�ǂP�ł���m�������߂�B
�ʂ̓���ꏊ�ɂ��āA�l�����Ȃ��ėǂ��A�Ƃ����C���[�W���킫�܂���
�ŏ��̔��ɐԋʓ����Ƃ����ꍇ�ɂ�1/19�~16/17�~6�ƂȂ�A���ꂪ10C1�~9C2������̂ł͂Ȃ��ł��傤���i�m����1���Ă��܂��܂����c�j
�ǂȂ�����낵�����肢���܂�
10*(choose(18,2)-9)/choose(20,4)
>>744
�����{��̏������悗
�����킗
�����Ɛ̂������Ă��Ă����Ƃ����
������đ呛�����邱�Ƃɂ���č��܂ł͂���ȕs���͍s���ĂȂ�������
�����������̂��ȁH
�ƌ������A�����������z�Ȏ��Ɨ����Ȃ�����r���������w������
���{���Ă��鎞�_�Ŏ����͂ǂ��������݂����Ȃ��́B
�����č�������ł�����������A���Q���͌��ɔ�ׂĕs�����ƌ����̂�
�̂���펯���������A�n��g�ُ͈�ɊȒP���������A�������������悤�Ȃ��Ƃ�
����Ă邯�ǂˁB ���̍���l�����ĂȂ��́H
���t�l���ǂ����p���ď������Ă�
�������v�����������ǁA���������Ƃ̉����ŃY�^�{���ɂ���Ă�
���t�{���E�̗L���҉�c�ő�g�����܂�
����R�c�ȑO�ɗ����̎d�g�݂��o���オ�������̂�����ɏo�Ă���
����Ȃ��Ƃ͍��܂łȂ�������

��{�c �厖�i�������Ɓj�ɂ���ȂƂ��������̈ӌ�
1�^5�ɂ͖�}�����J�Ȃ��烌�N�������Ă�
1�ނɎw�肵�čő���̑������A�\�Z�ψ���̏o�Ȃ��`�������nj��Ȃ������ăR���i�ɐ�O������悤�\�����ꂽ�̂���}
���J�Ȃ��d�����₷���悤�ɂ��Ă�
���t�l���ǂ����邩�琭���ɂ���ďȒ��̓����̓K���b�ƕς��
�����}�������{�l�ɂ͑I�����͂Ȃ�
����}�����̈����̎���ɂ��ǂ肽���l�Ԃ����邾�낤���H
�͂����肵���ΈĂ��Ȃ��̂Ɉ��{�����ᔻ����͖̂��ӔC����
���{�l�Ȃ炻��Ȕڋ��Ȃ��Ƃ͂��Ȃ�
�{���ɓ��{�̂��Ƃ��l���Ă��鈤�������Ƃ͈��{�������Ȃ�
�̂�т�ł炸���{����̐���������낤
�G�͒��Ƃ�p���N�ł��邱�Ƃ�Y�ꂸ��
�N���[�Y�D�ɂ��ẮA���J�Ȃ̔c���~�X�ɂ��l�Ђ��Ǝv���B
�D�̋t���[�}�ɂ��A�O�C�������30��
�c��70���͗z���҂̋q�����܂߁A�~�b�N�X���đS���ɍĂяz���Ă���B
���J�ȉ�ł́A�u�ʋŕ�������Ă��邩����S�v�ƌ���Ă������A�O�Ԉ���Ă���B
�ł�������������b�́A�e�D���͂�������Z�p���[�g����Ă���B�A���m�F���ꂽ��q�����̌�D���Ŋ������邱�Ƃ͂Ȃ��ƌ����Ă����B
���Ȃ��Ƃ���b�́A���܂��Ɋ��S�ʋƎv������ł���B
�����͂��łɔc�����Ă��āA������̓������͍I���Ɍ��ĂĂ���̂��낤�B
����͌��J�Ȃ̐l�ЂŁA���D��Ђɂ����K�̌̈ӂ̐ӔC������Ǝv���B
�t���[�}
https://pbs.twimg.com/media/ERI8GRPVUAE3z--?format=jpg ���{�������ƌ����Ă邩��Ƃ����ɗ\�Z�̑g�ݒ����ɂ͒��肵�Ă�
������}���T�N���K�[�Ŏז����Ă�̂��Ǝv���Ă���܂����̋t���Ƃ�
����Ⴝ�܂���
�������Y�}�ɔ����Ă���̂����{���Y�}�B
���{���Y�}�̕������ɂ͕ێ�ɂ݂���B
>>1
�y���]�����Ȃ��z
�E���{�����[�}���V���b�N
�E���Œ��肸�ɕ������Zww�V�K�̗p���~��20000�l�����X�g��
CMOS�Z���T�[���FLED�������Ɣ��pww�����̔��pw
�E�\�j�[�{�Д��pwww�@�E�\�j�[���o�C��2100�l�팸
�E�V���[�v�{�Д��pwww3200�l�팸www��p�g����w
�ENEC���C�e�B���O�ANEC�t���e�N�m���W�[�e�ГX�ܕ����X�g��ww
�E�j�R�������� �f�W�J����s�U1000�l�팸��
�E�x�m�ʐ��S���Ԏ�PC���Ɛ��ށA�������m�{�֓���ww
�E�����̃��[��55%�o�팸�v40���~�̐Ԏ�ww
�EPanasonic �t���p�l���P��ww�@�E���͓d�@1105�l�팸w
�E�I���L���[30���~�Ԏ�100���팸���E�T�����[�I���R�����E���{�R�����r�A�I���R����
�E�J���I�PSHiDAX�S�S�X��w�@�E�����ώ��i�T�O�X��w�@
�E���[���h�T�O�O�X�ܕ�w�@�E���[�\���Q�U�O�X�ܕ�w�E�_�˂��Ւ� �S�X�ܕ�w
�E���m�����P�O�O�X�ܕ�w�@�E�X�V���[�؍��t�@���h�ɔ���ww
�E���}�_�d�@42���~�̐Ԏ�w�U�O�X�ܕ�w�@�E���I�b�N�X��19�N12����22���~�̐Ԏ���
�E�R�W�}63��5000���~�̐Ԏ�w�T�O�X�ܕ�w�@�E���^�~�W�T�X�ܕ�w
�E�}�N�h�i���h�P�X�O�X�ܕ�w�E�C�I���P�O�O�X�ܕ�w�@
�E�����R���r�j �R�R�X�g�A�S�X�I��w�@�E��]���i�`�F�[�����������j�Y����w
�E�t�@�~���[�}�[�g��]�ސE�ҕ�W800���팸���A�S�Ј��P/�V��1,000�l����]�ސEw
�E�J�l���H�i19�N2�����ߋ��ň���8���~�Ԏ��A�H�ꌸ��
�E�����w�@�퉵�u�G���E�G���E�G�X�v�����Đ��@�A����66���~��
�E�T�[�N��K 1000�X�ܕ��{295�X�܁@�lj��X��
�E�Z�u�����A�C3000�����팸�A�Z�u���C���u��1000�X��
�E�C�g�[���[�J�h�[�S�O�X�ܕ�w�@����ɕs�̎Z33�X�ܕX����
�E���� �������S�O�X�ܕ�ww�@�E���j�[�T�O�X�ܕ�w
�E�T�[�e�B�����A�C�X�A40�N�Ԃ��Ԏ�ww�E�����`�J���߂��P�O�O�X�ܑS��w
�E�X�e�[�L�u�y�b�p�[�����Ȃ�I�X�e�[�L�v25���Ԏ�44�X�ܕ���
�E��藷�s�㗝�X �G�C�`�E�A�C�E�G�X�P�P��3200���~�̐Ԏ�w
�E���a��s�旧�s�\�A�u�J���R�[�|���[�V�����v�j�Y15��300����
�E���w���[�J�[HOYA ���Y�Ɩ��P��w�E��������Ɓu�疾�Ёv���ĕ���30���~��
�E�����t�@���hGENUSION�o�c�j�]20���~����w�@�E���{�����Y��JT1754�l��w
�ESEC�J�[�{��30���~�̐Ԏ�w�@�E�Z�F����69���~�̐Ԏ�w
�E��ˉƋ�43���~�̐Ԏ������z����w�@�E�O���[57���~�̐Ԏ�w�@�E����S��70���~�̐Ԏ�w
�E��Ë@��u�q���Z�d�q�v�j�Y�A����83���~���E�C�V��59���~�Ԏ��A00�N�ȗ��Œ�w
�E�j�b�Z��150�l�팸w105��5000���~�Ԏ�w�@�E�c�Ӑ��� �Q�T�T�O�l�ɑ����ގ�ww
�E�z�e���^�c�u���{�I�[�i�[�Y�N���u�v����������145���~��
�E�g���[�j���O�@��MTG267���~�̍ŏI�Ԏ����@�E�O�H���|160���~�̍ŏI�Ԏ����@
�E�W���p���f�B�X�v���C318���~ 4000���~�Ԏ��X�ܕ��E�����t�@���h�v��|�Yww�ŋ��D�_�W�cw
�E�R�R�X�i�j2���~�̍ŏI�Ԏ��A���㌸���@�E�W���C�t��15���~�̐Ԏ��A�q�����E�l�����
�EGAP�P���I�[���h�l�C�r�[���{����P�ނ֑S53�X��w
�E�V���h���[�G���x�[�^���{�P��www�@�E���Y������ �s�U���Y���l�I���R��ww
�E�g�c�S���t�j�]w�����z�P�U�U���W�V�O�O���~w�@�@
�N�\���{��W�Ђ��K����������Ȃ�w �W�҂��u�ł����|�����������v�Ƃ���2011�N3��15 ���́A
���������d�͖{�Ђɏ�荞��Łu�P�� �͋����Ȃ����v�Ƌ����Ƃ��Ēm���Ă���B
�}�슯�[����
�u����A�����̏������[���ȏ�Ԃɂ���B����ɉ����A���d���猻���P�ނ������Ƃ̐\���o���������B���@���Ƃ��ēP�ނ͔F�߂Ă��Ȃ����̂́A���ꂩ���w���Ԃ��[���������ꍇ�A�ǂ̂悤�Ȕ��f���Ƃ邩���߂Ă��������v�B
���i�`��Ȓ��������A����������������ȋC�������B
�Ȃ��ΓP�ނ������I�ɔF�߂邩�̂悤�ȓ����������B��u�̒��ق̌�A���������������Ŕ����B
������
�u�P�ނȂ�Ă��蓾�Ȃ��I�P�ނ�F�߂��炱�̍��͂ǂ��Ȃ�I�v
�u���d�̐����В������@�ɌĂׁv�B
�u����œ��d�������o������A�S�Ă̌������_���ɂȂ�B������ꂾ������Ȃ��A�����A����ȊO�̌������B����͓����{�S�����_���ɂȂ���Ă��Ƃ��B�v
�u�����Ȃ����獑�̑̂��Ȃ��ĂȂ��B����ȓ��{��������A��������Ǘ�����錋���ɂȂ�v
��������u�����ɓ��d�ɍs������A��������悤�ɁB�ǂꂮ�炢�����ɕK�v���H�v
�����d�͐����В����������l�q�������B
�����В��u�Ԃ��炢����c�v
�����u����ȗI���Ȏ��Ԃ͂Ȃ��I�v
�������u�c�v
�����u�ꎞ�Ԃŗp�ӂ��ĉ������B�ז�N�s�����܂��v
�����В��u�͂��c�v
���c�鏑��
�u���������A���������Ԋ�Ƃɐ[���Ȗ��߂��������Ƃ͏o����̂��v
�u�����{���̖@�I�����Ǝw���������͂����肳�����ق��������̂ł͂Ȃ��ł��傤���v
������
�u������A���܂���Ȃ��ƌ����Ă�ꍇ����Ȃ���I���{�����S�̊�@�����I�v
�u�����̌������̂��A����������鎖�́A���Ƃ��Đ��藧���Ȃ��B����ȍ��͑����ɐN�������B�v
�u�P�ނ��Ă��A���d�ׂ͒��B�������邵���Ȃ��v�B
�u�U�O�Έȏ�̐E���͑S�����n�ɍs���o��ł��B�����s���v
�������o���������_��
���������������R�͒����ό��q����Ȃ�
�������
�I�O��
1/5�ɂ͖�}�c���������ł̗��s�ɂ��Č��J�Ȃ��烌�N���Ă�
�P�����ɂ͖�}�����{����ݒu
�����͌��J�ψ���𗝎�������悢����J���Ɨv�����Ă��̂ɖ���
�d�����Ȃ�����\�Z�ψ���ɏo�ȋ`���̂�����J��b�̌��Ȃ�F�߂ăR���i��ɐ�O�o����l�ɐ\������
����
���ɂ��R���i�Ɋւ��Ă͐����œ����^�}�ɒ��Ă���
����̒��ǂނƂ�����
11���̗[���ɂ͂���IC(���p������)�����̔z�ǂɐ��f�����܂���IC���ق��J���Ă��쓮���Ȃ���ԂɂȂ��Ă���
IC�z�ǎ��̂��i�[�e������Ŕj�����Ă�\��
IC���Ôg���x���쓮���Ă��Ȃ����ɓ��d�͋C�t����
23:50�ɂ悤�₭�g�c�������i�[�e��̈��ُ͈�ɂ��Â��A������IC���쓮���ĂȂ���������m��
12���ɂȂ��Ă��珊��������Ɋi�[�e��x���g�����w��
1:30���@����x���g�̗�����A�}��̉��Ƀx���g�\��
�������}�����I����Ĉꎞ�Ԉȏソ�������_�ł܂��}�X�N���h�䕞������ɂȂ�
����Ŏ蓮�x���g�͔픘������Ď��t����
���̂��������K��@���ɂ���Ă���
�����A��������܂��x���g����
���̌�A��F���̔���������܂Ńx���g���Ȃ��Ɠ��d���猧�ɘA��
�x���g�ɕK�v�ȋ�C���k�@���Ȃ����ɋC�Â��B
��C���k�@�̎���4���Ԃ������Ă悤�₭�x���g����
�������x���g�����琅�f�������ɋt�����鎩���\���ɂ������@��
���������̂��Ƃ͓��d�̃}�j���A����}�ʂ���͑S���ǂݎ��Ȃ�
IC����~�������_�Ō����̐��f�����͕s���ł������ƍ���̒���
�}�j���A���̕s���AIC�ɑ���m���s���ƃx���g�z�ǂ̌��\���������̐��f���������������Ď�
����}���i�߂��~�������g��H�����̂Ă�
���Z�ɘa�ɂ��~���A�����̂ĂĒ����ւ̌o�ψˑ��g�����������ʂ����̏�
����}���i�߂��~�������g��H�����̂Ă�
���Z�ɘa�ɂ��~���A�����̂ĂĒ����ւ̌o�ψˑ��g�����������ʂ����̏�
�}�X�N�����������D���Ă����x�ߐl����������Ȃ������ł������֎~�̌��ʂ͂���
�y�ꂢ��V��g�̐V�^�R���i�E�C���X�����Ǒ�ɑ��鐭�{�ւ̗v�]�z
(1) �����̐��̏[��
�E�����Ώۂ͈̔͂��������g�傷��
�E����������������n���q���������ōs���Ă��錟�����K�͂Ɏ��{�ł���悤�\�Z�z������
�E���Ԃɂ��ϑ����Ďs�������x���ł������̐����m������
(2 )���S���Ďd�����x�߂�Љ�̍\�z
�E�ٗp�҂����ɂ��s���Ȉ������Ȃ��悤�Ɋ�Ƃɒʒm����
�E������̑�K�̓C�x���g���~�̗v���A����уL�����Z����p�̕��S
(3) �d�����x�ގҁA��ٗp�҂��������Ƃւ̍����I�x��
�E�K�ٗp�҂̌��ɑ��鏝�a���t���̎x����A�x�ƕ⏞�̑[�u
�E���c�Ǝ҂ւ̐����x��
�E�������Ƃ̎��Ǝ҂ɑ���A��ٗp�҂̋x�Ƃɂ��o�ϓI�����ւ̕⏕���̌�t
(4)���{�l��q�̎��q���{�݂ւ̈����Ԃ̊u���E�◯
�E�N���[�Y�D�̏�q�̑S�������݂₩�ɉ��D������
�E���D���Ɋ������m�F����Ȃ��Ă��A���q���{�݂�ܗ֑I�葺�Ȃǂ̎{�݂Ɉ����ԁA�o�ߊώ@�̂��߂ɑ؍݂��Ă��炤
�E���Ԓ��ɂ��Ă͐��{����u���������v���x������
(5) ���݂₩�ȏ���ł̌��łȂnjo�ϑ�
�E��Ñ̐��̍\�z���L�̗v�]�̎����Ȃǂ̑�ɓ��������\�Z�Ă̕Ґ������߂�
�E�R���i�E�C���X�ɂ��o�ϓI�����ɑ��A����ŗ����W���ɖ߂��ً}���@�}�h���ӂŐ���������
�E����ɒ������i�C��ނɔ����邽�߂ɁA�ł��邾����������ł��T���ɖ߂����Ƃ����߂�
(6) �\�h�I�[�u�Ƃ��Ē����؍ݗ��̂���O���l�̓����ꎞ�֎~�̐���̌���
�E��Ζk�Ȃ܂��͟��]�Ȃɑ؍݂��Ă������ׂĂ̊O���l��̓��{�ւ̓����֎~�ɂ��āA���₩�ɢ�����{�y�S�̣�ւ̑Ώۂ̊g��ɂ��Đ��{�Ɍ�����v������
(7) �펞����K�v�Ƃ���ݑ�̏d�x�Ⴊ���҂����������ꍇ�̑Ή�
https://reiwa-shinsengumi.com/reiwanews/4146 4���@�늳�҂̐��̌��\����߂�B
5���@�x���ƃC���t���̎��҂̑�������N�ƕω����Ȃ����Ƃ𗝗R�ɏI���錾
6���@�}�X�R�~���l�b�g���I�����s�b�N��F�B�R���i�̂��Ƃ��������ނƁu�R���i�]�v�ƕԂ���Ō�͍ݓ��F��
>>770
�㓡�c��������ł����B�v���]���Ċ��@�ɍs���āu�V�Ђ͂��傤���Ȃ��B�n�k�͐l�Ԃ̗͂ł͂ǂ����悤���Ȃ��B�����ǓV�Ђ��N��������̂��Ƃ͑S�Đl�Ђ��v�u���Ȃ��͐����Ƃ�����S�����Ȃ�������Ȃ��B���邱�Ƃ͂Ȃ�ł����Ȃ�������Ȃ��v�Ƃ����A�h�o�C�X�������̂ł��B
���R����͂����ȑΉ��������Ƃ��ɁA�����Ɋ�@�Ǘ��̒m��������킯�ł͂Ȃ�����ǂ��ӔC����邱�Ƃ��ł���A���͂��ꂪ���[�_�[�Ƃ��Ă��̂�������Ȃ��ƂȂ̂ł��B������b�ɂ����݂��ĂƂ������Ƃł͖����ł�����B�������������̂ĂĂł����ł�����ƁB
����ʼn�����������ƌ����ƁA�����}�̏����嗘����Ȃǂ̐l������S������ɔh�����āu�S������Ō��߂Ă���A���ꂪ��ԕ��������B�@���ł��낤�����ł��낤���A������Ђ�����Ԃ��Ăł����ꂪ�K�v���Ǝv�����͑S�������ӔC����邩�����Ă���v�ƁA���������̐���������̂ł��ˁB ���{�������Ă����͓̂O�ꂵ�ăA���`�m���Ȃ��
������w�̌����\�Z�팸�A�����Ǒ���p�̍팸�A���Ƃ̏����͖������Č�p�w�҂̂N�p
�j�b�|�����g�������X�I�I���Č����Ă��A�z���M������킯�ŁA�����ɁA�n���ɍ��͂��グ�Ă����Ȃ�Ĕ��z�͖���
�A�x�m�~�N�X�ɂ��n�����ŏo�������ߋ��Œ�B
�P�����s���Ă���Βa�������͂��̓��{�l�����{�͉��l�E�������ƂɂȂ�̂��낤�B
���̐M�����������s�̍ő�̌����F
���{���A�I�����s�b�N�J�Â���ێ��̂��߂�
�����Ґ��𑝂₵�����Ȃ�����A���������肵�Ă������ƁB
815 �F�n�k���Ύ�������(�����s) [sage] �F2013/07/12(��) NY:AN:NY.AN ID:Vr4sb58l0
�����������̂̋��P�́A���{�Љ�Ő�����Ȃ���{�W�O�═���t�F���[��
���������В��̂悤�ɐ�����̂�����ŁA�����l�݂����Ȑ�������
�����Ƃ������ƁB
�Ƃ�킯���������w�Ԃׂ��Ȃ͕̂����t�F���[�̗������̂��܂��B
���d���猴���̐��ƂƂ��Ċ��@�ɔh������Ă����̂ɐ����l�ɑ���
�����������A�ނ��됛���l�̈ӂ�����ŗ�����邱�Ƃɐ�O���A�����̐��Ƃł�
�����l���ɂ܂�鋰�ꂪ����Ί��@�̋�C��ǂ�ŋg�c���������Ē������~������B
���̓`�������A������~�͎����̎w���ł͂Ȃ������܂Ŋ��@�̎w�����Ƃ���
�`�ł����A����ɓ��d�̍L��Ȃǂ��g���āu�����l��������~�������v�Ƃ���
�����}�X�R�~�⎩���}�c���ɂ�����Ă����B
���������ЂƂЂƂ̒��J�Ȏd�������{�Љ�ł͑傫�ȕ]���ށB
�����l�͕��������������{�l�Ƃ������ƂɂȂ��đ����̍���ǂ��A
���d�T�C�h�Œ�����~���w�������������͍��ی����J���̎В��Ƃ���
���{�����̉E�r�Ƃ��Č����̗A�o���d���Ă���B
(�ȉ����p)
������Y�́A�����d�͂Ƃ����g�D�̒��ŁA����ł͐����Ԃ���J��Ԃ����݂̒n�ʂɔ����オ�����A
�s���g�̃]���r�Ȃ̂ł���B
�v���N�����A���̔��芠�H���q�͔��d���̏����߂Ă��������i�W�N�قǑO�j�A�_���E��C��ƂƂ�����
���S��ɉ����ċɂ߂ďd�v�ȋL�^���B���y�яC���������ƂŁA�����U�����̏������Ă����B
���̌�A���̂��햱������i���q�͒S���j�ɏ��i������A�ēx�A�f�[�^�[��������݂ƂȂ��āA
���̐ӔC�������R�����̏������邱�ƂɂȂ�B�펯�����Ƃł���A���̓x�d�Ȃ鏈����
�����ƂŁA������Y�̊�Ɛl�Ƃ��Ă̗���͎�����̂����ʂł���B
�������A������Y�͊��x���̒v�������Ȃ���A��̐V�������z���n�k���������钼�O�ɁA
����В��ɏ��i���ʂ����A���ی����J���В��ɓV����o�����B
���{�Ő�����Ȃ�A�������̐��������悭�������Đl���̎w�j�Ƃ��ׂ��B
���̐�͏d�lj����Ă�ނ����������l���������҂ɃJ�E���g����Ȃ��Ȃ�A�R���i�����I���{�͈��S�ł��I���Đ��E�ɃA�s�[�����ăI�����s�b�N�B
���Ŕx����S�s�S�ő吨�̎��S�҂����Ă��������ꎟ��ɂ݂�ȖY��Ă����B
�����Ɠ����p�^�[�����B
���{�͎��s���Ȃ��Ō��ʂ��o��������
���{���̎������Ă�����}���P�`������
�͎����𐔔{�Ɍ�����t�F�C�N�𗬂�
�Y�o�ǔ��ʼn��Ƃ��y��_���ꂷ����x����
���卑�����ƑΓ��ɂ���Ă�ɑ��̂��Ƃ�
�����ȋt���z��ɗ����o����͂��͂Ȃ���
�U�v�̎��Ƃ͈���Ă������E���x���Ȃ�
�������瑡�^���ꂽ�����L�b�g�����Ǝg����
�����Ґ����l/���������������o���Ȃ���
�摜���{�����m��ǂ�
���ƋƂȂ̂Ɏ�����HP�ɍڂ�����
��W�ɏ��̃o�C�g�ł����ď�������
�{���������瓪�����Ȃ�Ă���Ȃ��A����Ȃ킯���Ȃ���
�����炳�܂���������t�F�C�N�Ƃ��Č����Ă�����
������a�ɂ��ė��Ő��_���삵�Ă�ƍl����ׂ���
���m�ȓG�����A������U�����邱�ƂŒ��Ԃ̂悤�Ɏv�킹�Ȃ��珙�X�ɗU������
����������������܂��̎d���͐��_�Ȃɒ���I�ɒʉ@���邱�Ƃ���w
������h�̎R�䂪�u�N���[�Y�D�����O�����������������āv���Ď��O�ʍ��t���Ŏ��₵�����ǁA
�����́u�c�����ĂȂ��A���������o���Ȃ����Ƃɂ��Ă���v�̈�_����������
>>783
���܂����H
�^���q��ɂ͌����ĉR�����Ȃ����q�吶�ƕK���R�������q�吶�����邱�Ƃ��킩���Ă���B
���̏��q��̊w���i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�Ԉ���Ă���Ή������Ă����Ȃ��v�ƌ���ꂽ�B
���q�吶�Ƀt�F�������Ă��炤�ɂ͉��ƌ����������H ��҂ł͂Ȃ����܂��̘b�ɂ͐����͂��Ȃ��@�n�n�n�n�@�ȁA���䌧 �z�O�s �Z�����t�n�n�n
���܂��͎厡��̐搶�̎w���ɏ]���Ă�Ⴂ���́B�n�n�n�n
>>787
���̎Ⴂ�������C��i�R�����ǂ����͕s���j����
�u���Ȃ��̂������Ƃ���������Ύ�R�L���t�F�������Ă�����A�����łȂ���Z���Y���𖽂���v�ƌ���ꂽ�B
�t�F�������Ă��炤�ɂ͉��ƌ����������H
�������Ȃ����ăA�z�Ȃ́H�@
�t�F�����Z���Y�����D���Ȃ́H
�ǂ����H �����̎��̐����l�̑Ή���BBC��h�C�c�Ƃ��C�O���f�B�A�ł͏̎^����Ă��̂ɂ�
�����Ȃ��ɂ݂�����Ȃ���Ă��Ƃ�
���䌧 �z�O�s �Z�����@�������������i�ł��Ȃ�������]�ɂ����Ă��Ȃ�www
���ā@�����̃J���t�@�����X�̏����ł����邩��
>>792
�����V���c�̓t�F�����̓��܂��H
�Z���Y���̕����D���Ȃ́H >>793
�J���t�@�Q���Ƀt�F�����̓��������Ă�����Ă��������H
�S�������o�J�Ȃ̂��H �����}�ɂƂ���
�J�W�m���������������̖�
�{�{�O
@miyamototooru
�\�Z�ψ���ŗ����Љ�h�Ɠ��{���Y�}�ŗ\�Z�g�݊�����Ă��s���A
�J�W�m�֘A�\�Z�A�}�C�i�|�C���g�֘A�\�Z2516���~����߁A
�V�^�R���i�E�C���X��ɐU������邱�Ƃ����߂܂����B
�c�O�Ȃ��玩���E�����E�ېV�̔��Ŕی��B
���N�x�\�Z�ɂ͐V�^�R���i��͈�~���Ȃ��B��_�ȑłĂ�̂��B
�ߌ�1:57 · 2020�N2��28��·Twitter Web App
����Ȃ̂��܂��ɂ͂ǂ��ł���������@���_�a�@�֍s���Ă��� w
>>797
>>792
�����V���c�̓t�F�����̓��܂��H
�Z���Y���̕����D���Ȃ́H ���䌧 �z�O�s �Z�����@���܂��̎d���͐��_�a�@�ɒʉ@���邱�Ƃ���@���܂��̍l���Ȃ�ĒN����������Ȃ���B���n�n�n�n
>>800
>>793
�J���t�@�Q���Ƀt�F�����̓��������Ă�����Ă��������H
�S�������o�J�Ȃ̂��H
�Z���Y����]�Ȃ̂��H ��͂葽�Q�͕����𗝉�����̂��x���B�����ė���͂��s�\���Ȃ̂ō��{�I�Ȗ₢�ɓ������Ȃ��B���n�n�n�n
�ꌩ�J�b�R�ǂ������Șb�����Ă��@�悭�����Ƃ����Ɨ������Ă��Ȃ����Ƃ��o����B�t�n�n�n
�����瑽�Q���邵�A���������i�ł��Ȃ������ȁ@�A�n�n�n�n�[
>>805
>>797
�����V���c�̓t�F�����̓��܂��H
�Z���Y���̕����D���Ȃ́H �J���t�@�Q���҂��S���h��ӃV���c��Ȃ̂��H
�Z���Y����]�Ȃ̂��H
�@���{�ł͍��A�o�ϑ�Ƃ��ĐV�K�̕�\�Z��g�ސ������܂��Ă���B26���ɂ͎����E�����̗��}����
�{�����Ɍo�ϑ�̍�������߂���j������B�ł́A��p�͂ǂ����B��p���@�@�i����j��25���A600����
�p�h���i��2200���~�j������Ƃ���o�ϑ�̓��ʗ\�Z�Ă��������B�傫�ȑŌ����Ă���ό��Y��
�ւ̎x���Ȃǂ����ɂȂ�\�肾�B
�@���̂ق��ɂ������ւ̃}�X�N�A�o�֎~�⌵�����n�q�����ȂǁA��������X�Ƒł��o�����j�ɓ����͔�
�����������B����ł��A28�����݂Ŋ����Ґ���34�l�ɗ}�����Ă��邱�Ƃ���A�ᔻ�͏��Ȃ��Ȃ��Ă���B
��p�ł́A2003�N�ɋN����SARS�i�d�Nj}���ċz��nj�Q�j��84�l�̎��҂��o�����B���̎��Ƃ̈Ⴂ���A��
���]���Ă��闝�R���B�����̐����قȂ邽�ߒP���Ȕ�r�͂ł��Ȃ����A���{�̊����Ґ�210�l�i�N���[
�Y�D�̗z��������705�l�������j�A�؍���2000�l�ȏ�i�������28�����݁j�Ɣ�r���Ă��A�����_�ł̕���
���ߑ�͈��̐��ʂ��o���Ă���Ƃ����邾�낤�B
�@��p�ݏZ�̃m���t�B�N�V�������C�^�[�̋ߓ��퐶�q����́A�����b���B
�u��ʂ̐l�X���s���Ɋ����Ă��邱�Ƃɂ��ď�ɐ��肵���Ή������Ă��邱�ƁA�����������h��
���s���@���i�ɑ����j���Q��Ԃ�ɂ���ŕK���Ɋ����NJg��ɕ������Ă���p���`����Ă��܂��B��
������`���[�^�[�@�ŋA��������p�l�����l�̊������m�F���ꂽ���́A�����q�����������i�ی����j
���L�҉�ŗ܂𗬂��Ȃ���w���҂̐��͑����Ăق����Ȃ��B�����A�t�ɍl����Ɩ����~�����Ƃ��ł�
��x�Ƒi���A���̐^���Ȏp�ɑ�p�l����̎^�̐����������܂����v
�@�g�_�Ή��h��A����������̂Ȃ��ŁA���E���璍�ڂ���Ă���̂��f�W�^���S�������ψ��i��b�ɑ�
���j�̃I�[�h���[�E�^���i���P�j�����B�^�����͐��E�I�ɗL���ȃv���O���}�[�ŁA����38�B8����v��
�O���~���O���w�сA14�Œ��w�𒆑ށB15��IT��Ƃ��N�Ƃ����B���̌�Ƀg�����X�W�F���_�[�ł��邱
�Ƃ𖾂����A36�œ��t�������͐��ʗ��Ɂu���v�ƋL�������B�^������IQ180�Ƃ�������V�˂ŁA��p��
�l�X�́u�ޏ��̑��݂͎������̊�]�v�ƕ炤
2/29(�y) 7:00�z�M
https://headlines.yahoo.co.jp/article?a=20200228-00000078-sasahi-soci&p=2 �o�J�u���{���t�����E���āA���{�̑��肪����́H�v
�E����������₂��Ȃ��l
�E���v���U�����Ȃ��l
�E���Љ�͂��g���đI���W�Q���Ȃ��l
�E�ŋ��ŗL���҂����Ȃ��l
�E��b���ʂ���l
�E�|�������ƍ��낶��Ȃ��l
�E���k�O���ƍ��낶��Ȃ��l
�E���F�B�����D�����Ȃ��l
�E�R�̗��R�ő��ł��Ȃ��l
�E�����Ǒ�3���ŏI��点�Ȃ��l
��������ł����邾��
��
���܂��@�������N�l����Ȃ��l
�����������v����`��Ƃ��ȁB
���w�̖��̕����y�����ˁB
�����͂������������ĂȂ���B���_�����ɂăh�N�^�[�X�g�b�v���B�q�q�q
��w����{���ő��Q���Ă���Ɠ��w���Ă���@���N���J��Ԃ��ăM���M���ő��Ɓ@���������x�Ă��s���i�B���̌�����Ă��Ȃ��B���͒�E�ɂ��Ă��Ȃ��J�X�ł��B���_�Ȏ�f���d���ɂȂ��Ă���B���n�n�n�n
���͑��������ł��B�J�b�R�����͂��邪�ˁ@���n�n�n�n
�ǂ������Ǝ킪�x�Ƃ���z�肩���킸�ɋx�ƕ⏞���������̂��đ����ň���
����Ȃ̂ǂ������������E�`���E�`���ŋx�Ƃ���̂��ڂɌ����Ă�
�ŁA�F��ȍ����̋@�\����Ⴢ��Ă���
�u����ȂɈ�Ăɋx�Ƃ���Ƃ͎v��Ȃ������v
�u�z���ꡂ��ɏ��錏���ł����܂ł̗\�Z�͂Ȃ��B�⏞�͈͂͌�����v
�Ƃ������o���̂��ڂɌ����Ă�
>>817
�܂��A�t�F�����̓����o���Ȃ��Ȃ��H
�Z���Y����]�H �����Ď�����5���߂���
����ł⏊���ŁA�Z���ŁA�Љ�ی����Ă����Ă������
�������̔�₵�ɂȂ��Ă��B
�~���X�}�̎��͎����͒Ⴉ������������Ȃ���
����ȂɎ����Ă�����Ȃ���������
����ł̓~���X�}�̎��̕����ゾ�����B
2017�N6��5���O�c�@���Z�s���Ď��ψ���
�ψ�
���āA������x�����܂�����ǂ��A�����́A������������������ӔC���Ƃ�Ƃ����������A�O���\�O���A
�Q�c�@�\�Z�ψ���ł���Ă��܂�����ǂ��A�����A�ӔC�Ƃ͂ǂ������Ӗ��ł����B
���������������ؖ����ꂽ��A�ǂ�ȐӔC���Ƃ��ł����B
���{
�ł́A�F����̂Ƃ��́A�\�����v����Ƃ����̂͏オ���Ă�����w�߂��画�x�ł����B�Ⴂ�܂���ˁB
�オ���Ă�����w�߂��画�x�ł͂Ȃ���ł��B
�i�����j���́w�߂��画�x�ɂ��Ă͌��t�Ƃ��Ė�肪����܂����̂Œ����������Ă��������܂����i�����j
�ǂ�Ȍ���ɂ����Ă��A���̌���ɖ�肪����̂ł���ΐӔC���Ƃ�Ƃ����͓̂��R�̂��Ƃł��낤�Ǝv���܂��B
�ψ���
���{�����A����ɂ��������������A�ӔC�Ƃ͉����ƁB
�ψ�
������A���̐ӔC�Ƃ͉����ƕ����Ă����ł��傤�B��߂邱�Ƃ��ӔC�Ȃ̂����Ȃ̂��ƕ����Ă����ł��傤
���{
�ӔC�����邩��A���̐ӔC���Ƃ�ƁB���g�ɂ��ẮA�����Đ\���グ��K�v�͂Ȃ��Ǝv���܂��B
���{�u�ӔC�Ƃ����I�v
�����u�ǂ��ӔC���Ƃ����H�v
���{�u�����Ȃ����ǂƂ����v
���{����͐���t����Ă��H
�ׂɗ]�T�̃A���_�[�R���g���[������
��������Ȃ̂͏K�ߕ��A���{����Ȃ���H
��ɂȂ�̂����Ȃ��Ѝs����A���C������
����͌����Ȃ��E�B���X�A���{����ǂ�����Ă�
�ł�����Ȏ��ɐ��{�ᔻ�͕s�ސT����}�W��
�������Ƃ̈ӎ����Ⴍ�Ȃ��H
�ł�ł��炶��ǂ����悤���Ȃ������
�Ԃ����Ⴏ�C���t�����y������
���Ȃ݂ɈېV���������}������A�I���̎��͋C��t���悤��
�{�{�O
@miyamototooru
�\�Z�ψ���ŗ����Љ�h�Ɠ��{���Y�}�ŗ\�Z�g�݊�����Ă��s���A
�J�W�m�֘A�\�Z�A�}�C�i�|�C���g�֘A�\�Z2516���~����߁A
�V�^�R���i�E�C���X��ɐU������邱�Ƃ����߂܂����B
�c�O�Ȃ��玩���E�����E�ېV�̔��Ŕی��B
���N�x�\�Z�ɂ͐V�^�R���i��͈�~���Ȃ��B��_�ȑłĂ�̂��B
�ߌ�1:57 · 2020�N2��28��·Twitter Web App
���Ȃ݂ɈېV���������}������A�I���̎��͋C��t���悤��
�{�{�O
@miyamototooru
�\�Z�ψ���ŗ����Љ�h�Ɠ��{���Y�}�ŗ\�Z�g�݊�����Ă��s���A
�J�W�m�֘A�\�Z�A�}�C�i�|�C���g�֘A�\�Z2516���~����߁A
�V�^�R���i�E�C���X��ɐU������邱�Ƃ����߂܂����B
�c�O�Ȃ��玩���E�����E�ېV�̔��Ŕی��B
���N�x�\�Z�ɂ͐V�^�R���i��͈�~���Ȃ��B��_�ȑłĂ�̂��B
�ߌ�1:57 · 2020�N2��28��·Twitter Web App
>>41
�����́u���������v�Njy����̃X�s���ړI��
�`���[�^�[�@�Ƃ��Ōy������Ă銴���݂��A�킴�ƃR���i�����҃����[�X����
���̃p�j�b�N�������N�����Ƃ����̂���ƈ��{�̈Ӑ}�ł����B
�v�͐W�דI�����g�傾�����킯�Ȃ̂ł��B
�Ƃ��낪�A�����̂悤�ɗ��ڂ��āA
�p���f�~�b�N�����ăI�����s�b�N�J�Â������@����
�C�Â��₢�Ȃ���j�]�����܂����B
�܂�A�����\�����ۏ�������g�������v�U���ɂ��A
�����Ґ��}���H����n�߂��̂ł��B
���̌��ʁA��ƈ��{�͎���g���������҂ɑ��āA
���낤���Ƃ�������F�߂Ȃ��Ƃ����s��ׂɂ��A
�������E���Ƃ����ƍ߂����ł����Ă��܂��B
�v����Ɏ�ƈ��{
�ߕߎ��Y�E�����`���E�V�F�X�N
��E��Z�ł͐��ʂ邷��
�S�E�K�� ���Q�����͂������Ȃ��@�����̐g�̏�ɍ�������w�ɓ��肽���@��ŋ�J����̂������邩��
��������Ă��@���Q�͗�O�Ȃ��@���������@
�����ō�����w���i���e�Ƃ̈Öق̗����������ȁB
����Z���ゾ��������͎�����A�̗�I�ƈ�Ȏ��Ȃ�I���B
���l�̍������ɐi�w�B
>>829
��c�̎�����Ƃ���������ˁB ���A���������l�͌����Ȃ�Ŏ��炵�܂��`
���̈����l�Ƃ�����
�܂��A�t�F�����̓����o���Ȃ��h��ӎ�����B
�Z���Y����]�H
���������̊C�N�s��̏o����������S�z�Ȃ�
���������̏o����������S�z�Ȃ�
�����̏o����������S�z�Ȃ�
�t�ߊ��}
�l�q�g�������Ȃ�����S�z�Ȃ�
���{�l�ɂ͂���Ȃ�����S�z�Ȃ�
���{�l���m�Ŋ������Ȃ�����S�z�Ȃ�
���{�l�͌������Ȃ����犴�����Ȃ�
����������S�z�Ȃ�
�G�A���]�������͋�C�����łȂ�����S�z�Ȃ�
�������Ă��d�lj����Ȃ�����S�z�Ȃ�
���ʂ̂̓W�W�o�o������������a�C����������S�z�Ȃ�
�q���͏d�lj������莀�肵�Ȃ�����S�z�Ȃ�
4����5�����ɂ͏I�����邩��S�z�Ȃ�
�v�����͂�����C���t���G���U�ƕς��Ȃ��Ȃ邩�猟�����Ȃ��Ă��S�z�Ȃ�
�d�lj����������Ĉ�Õ��Ȃ���ΐS�z�Ȃ�
�}�X�N�͌��ʂȂ�����S�z�Ȃ�
���������l�̂V�T���͑��̐l�ɂ͂����Ă��Ȃ�����S�z�Ȃ�
����Ԃ������ΐS�z�Ȃ�
�č��܂łɂ͏I�����邩��S�z�Ȃ�
���҂�56���͔��M���Ȃ�����S�z�Ȃ�
�d�lj����Ă��l�H�ċz��m�ۂ���ΐS�z�Ȃ�
���x�ɂ悢���ǐS�z�Ȃ�
���Ǐ�ɂ�������炸�A�E�C���X�ʂ͔��ǎҕ��݂����ǐS�z�Ȃ��|�|�|�����R�R
����p�̃R���i��
�E������0�ł�1��15���ɂ͎w�芴���ǂ�
�E�����؍ݗ����B���Ɣ���110���~
�E�����l�̓�������
�E�}�X�N�̗A�o�֎~
�E�}�X�N�̓]���֎~�A�w���͎�����
�E�}�X�N��a�@�A�ʉ@�҂ɗD��z�z
�E��Ƃ��L���̎擾���ۂ����珈��
�E��ǂɂ���}�X�N�̍Ƀf�[�^���C���^�[�l�b�g��Ɍ��J
�E�}�X�N�ɏ��킩��A�v�����J�����Ė����z�z
�E�y�[�p�[�Ɋւ���f�}�𗬂����A����6����ߕ�
�E�V�@�{�s���f�}�g�U�҂�������
���{���Ă�������������ĂH
�v�g�n�u�����̑Ή��͊����B
���j�Ɏc��ϋɓI�ȕ������ߑ����B
���{�̂����Ő��E�Ɋg�U���Ă�v
���ꂪ������WHO�̃V�i���I
���Ɖ�c�ł͋x�Z�ƈꌾ�������ĂȂ������ꂩ��1�A2�T�Ԃ����ˍہ��S���ꗥ�x�Z�ɂ��܂�
���̎��o���ˁH
�����u�}�X�N�͂����ɏo���悤�ɂȂ�܂��v���ĉR�����̂��v�����ɂȂ����ȁB
����̂����Ő��{���g�C���b�g�y�[�p�[�Ȃ��Ȃ�܂�����Č����Ă��N���M�p���Ȃ��B
�������ŕĂ�p�����Ȃ��Ȃ��Ă����B
�ł��܂炠�肦�Ȃ����Ȃ����
���{����Ƃɋx�݂𐄏����Ă���Ă��Ƃ́A
�g�C���b�g�y�[�p�[���Ă��p�����x�Ј��̕��������Y�ʂ�����̂͊ԈႢ�Ȃ���
�X�[�p�[�����Ă��Վ��x�ƂɂȂ��Ă����������Ȃ�
>>839
�������Xw
�W�C����̍����甽�����N�l�̗��ꖡ >>829
���Q�⏗�q�͓����̎��_�œ_�����������Ă�̂ł��傤���Ȃ�����B
���N�O�̎����̗����������Ŗ���݂ɂȂ��������B
�����܂������̂̓p�p��������������Ȃ�������{���͈�҂ɂȂ�Ȃ�����
��ӗ���������呲�̘A������B
�ŋߒ�ӎ������̃��x�����オ���Ă����ƌ����Ă�̂́A����⋞���
���Ƃ��Ă�������Љ�ɏo�����ǐS�ς�肵�Ē�ӎ������ɓ��w������҂�
�����Ă������炾��B
�ނ�ɂ��Ă݂�A�������ӎ������𑲋Ƃ��Ă��A���X���呲�⋞�呲
�Ȃ̂ŁA�ނ炪���������ƍl����l�͂��Ȃ����낤���A�ނ�͈�t�Ƌ���
���߂����̖ړI�Ȃ�A�킴�킴��ւȍ��������ɓ��邽�߂̎���
�Ăюn�߂�̂��ʓ|���������A�������Ζ����n�т̒�ӎ������ŗǂ���I
�Ǝv���Ă��B
�v����Ɉ�t�Ƌ������Ƃ��ړI�Ȃ̂œ��w���₷����w�ɏW�܂�͎̂��ɓ��R�B >>842
����Z����̓��w�����ǂQ�����炢���Ďg�B
�قƂ�Ǔ��呲�����呲�B���͊w�m���w�����������������Ȃ������悤�Ɏv���B�w���җp�̑̈�����������l��������Ȃ�����̂ʼn����싅�ɎQ�����Ă����B ���T���鍂�Z���ł����A����Z�Ȃ�đ�w���͕��������Ƃ�����܂���
���O���m���Ă��Ȃ�F�����Z�ł����H
��ӎ������𑲋Ƃ�����҂��ē�������ˁH Part14
�˂����킯�˂�����i�{�j�I�I�I
>>844
����Z����͓���ƈ�Ȏ��ȂƗ����ł�������A
����ɍs�����Ɉ�Ȏ��Ȃ�I�������B
�����I�������������������ȁB

>>845
����́A�h��ӃV���c���̑��@���Ƃ��Ēm���Ă���܂��B
�h��ӃV���c��傪�����̂ł͂Ȃ��A�{�l�̓��������B >>844
����Z�E����Z��60�Έȏ�̂��ꂿ����̓����̍ۂɎ�������Ă�
�����̕�������B�ڂ����͒m��ǁA����������Z�Ɠ���Z��2�O���[�v��
�����āA������������2���ꂽ��Ȃ����������H
�ł������͈��̐������Ȃ��������A���������f�R���������̂�
����̍���荑���̈�w���ɍ��i����̂���������͎̂�������B
�����͒m���B �m��\���̋G�߂��ȁB
���{�̊j�����Ɏg����Ȃ�[���ł�����A�h��ӃV���c���̎��w�������ɉ��̂��Ǝv���Ɩ��N�A�E���U������B
>>848
���̂Ƃ��͔{���P�X�{�������B�s��̃L�����p�X���Ɠ��肫��Ȃ�����A
�����͑�X�[�~�i�[���������Ȃ��B�\���Z�̋����̍L���ɂт����肵���B ����Z�E����Z����͐e�ʂ̃I�W�T���̎��ゾ�ȁB
�I�W�T�����Q�l���Ē�����w���𑲋Ƃ��ĊJ�Ƃ��Ă�B
������w����w�Ȃ���������213 [���f�]�ڋ֎~]©2ch.net
http://2chb.net/r/kouri/1454692118/319
319 ���O�F��w�ւ̖���������[] ���e���F2016/02/11(��) 22:52:02.21 ID:50TBuVXh0
�p�������Ȃ�����͂����̐e�������Ȃ�ł�
�������ł���
�{�l�͉B���������Ă������Ǒc�����������Ă������
�c���͑��q�i�����̕��e�j�̊w�͂Ȃǒm�炸�ɐi�H�w���œ�����O�Ɏ����̏o�g���i�����j����]�������e�̒S�C�ɖ������ƒf�����ꂱ�ꂪ�ꐶ�ōő�̋��J�����������ł�
�c�������\�N�������Ă�̂Ɏ��ʂ܂őc������̎��Ŏ�����Ă܂���
���O����������������Ȃ����炱���Ȃ������Ƃ�
�����͋���Ɏ��s�������c���̌���
���ꂪ�����w���n�a�̔߂�������
���ꂪ�����ł� ����B
���ꂪ�U��Ȃ������B
���كV���c��ƉƑ��̈ꐶ�A������B
���䌧 �z�O�s �Z�����@�݂�Ȏ����Č��Ă邼w
�ց[�A�܂����Z���Ă����͓̂�Ԏ�ȉ��Ƃ����Ӗ���
���ł����e�����ɑ��������ł��˂�
���ID:MOd/ilOT����͂��������̃X���ŘA�����Ă܂�����
���̓���̕��݂����ȕ��Ȃ�ł���
2020/03/08(��) 23:07:59.60ID:IUbeuTZ5 �u���������Ȃ��ق������҂��a�@�ɂ��Ȃ��̂ň�Õ��Ȃ����炢���v�Ƃ��A
�u�U�A�������邩�猟���Ƀ��\�[�X�����̂͊ԈႢ�B�Ӗ����Ȃ��v���Ă����Ă���炢����ȁB
���������́A
�������Ȃ������Ŋ����Ҍ����Ƃ��ĉ@�������������A�X�^�b�t�S�O�l����ҋ@�ɂȂ����B
�������Ȃ��ق�����Õ���p�^�[���ɂ��Ȃ���̂���B
������A�����J�Ƃ����u�����L�b�g������Ȃ��I�v�Ƃ����đ�ʂɑ��Y���Č������Ă���킯�łˁB
�@
�����^��������l���A
�a�@�֍s���̂ƁA�ƒ�ɂ���̂Ƃǂ����������g�債�Ȃ����B
����͂�����Ƃ������l��m���ŃK���b�ƕς��
��T�Ɏ���ҋ@�������Ƃ�����Ȃ����A�a�@�ւ����̂��K�����������킯�ł��Ȃ��B
�����҂�Ō�t�̐��A�ҍ����̐l���A��Î҂̑����A�����L�b�g�̊m���A
���̐l�̕a��⓯���̐l���A���̐l�̉Ƃ̑傫���A�N���̗́A�����������ϐ���������ƕς�邾���ōœK�����ς��B
���ꂪ������Ȃ��Ɛ��Ƃł��Ԉ�������ƌ����Ă��܂����A���\���{�݂����Ȍ��������ڂ邱�ƂɂȂ�A���ׂ���̂Ƃ�ׂ��^�C�~���O���킷��B
�����͂�������Ƃ����B
�������Ăق����Ƃ������l�͗\������Đ撅���ɂ���B�i�L���j
��������t���d�ǂƂ݂Ȃ������҂��D��B�i�����j
����Ō����̕K�v���Ȃ��Ƃ����l�͗\������Ȃ����A
�������Ăق����l�͗L���ł��������肤���A
�\�Ȃ̂őҍ���������Ŋ������L���邱�Ƃ͂Ȃ����A
�d�NJ��҂��D�悳���̂ŁA�������K�v�Ȑl�ɂ܂��Ȃ��Ȃ邱�Ƃ��Ȃ��B
���܂��͎Љ�̒�ӂɂ��ē��������̂�����@�����̎d���𑁂��T���Ȃ����B�܂��͐l�ԊW�̂Ȃ��P����Ƃ��炾�ȁB���_�Ȃ̎厡��ɕK�����k������@������