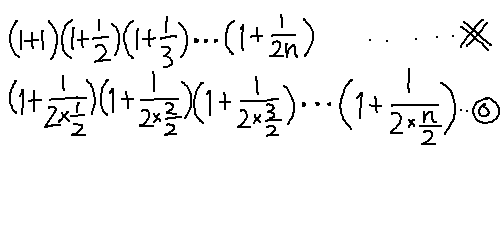�@�@�@�@�@�@�Q�Q�Q
�@�@�@�@�@ /:::::::::::::::::::�R
�@�@ �@�@�@l/�O_,�R,_:::::::::::�j�@�@�@�P��
�@�@�@�@�@���@�E�ցE�j�P�L �@�@ �`���[�n���Ȃ�Đ��w��炸�ɍ���Ă�������
�@�@�@�@�@/~�R �G i�@)
�@ �@�@�@(��'�i��Ɂ�)
�@�@�@�@�i�Q�j�@�@�i�Q�j
���͑����������邵���o���Ȃ�
�w���f�ϕ��ɂ�肠��͈͂�f�̒�ϕ��̒l�����߂���Ȃ�A����͉�������̍H�v�ɂ���Ď����̃��[�}���ϕ��ł����߂���x
�͐^�ł����H
�u�O�p�`ABC�ɂ����āACA��BC��a�A��CA��ɓ_P�A��BC��ɓ_Q������B�O�p�`CPQ���O�p�`ABC��1/4�ƂȂ�悤�Ȑ���PQ��̓_�̗̈�����߂�v
�O�p�`ABC���݊p�O�p�`�̏ꍇ���܂߂Ăǂ��Ȃ邩�����Ă�������
ek + 9kk ���������ɂȂ�Ȃ����Ƃ��ؖ��ł��܂���B
k�͐������ŁAe�͐����ie��0�j�ł��B
�m�O�X��.939�C941�n
e = -8k �̂Ƃ� k^2
e = -5k �̂Ƃ� (2k)^2
e = 7k �̂Ƃ� (4k)^2
e = 16k �̂Ƃ� (5k)^2
e = bb-9k �̂Ƃ� kb^2�@(b��0�Ck�͕������Ɍ���)
e = b(b�}6��k) �̂Ƃ� k(b�}3��k)^2�@�ik�͕������Ɍ���)
�m�O�X��.956�n
�k���983�l
���� 0 < x < ��/6 < y < ��/2 �ɑ��āA �s����
�@sin(x)/sin(y) < 2x/(x+y�j
�������B
�m�O�X��.983�n
>>9
e = (nn-9)k�@�in�͎��R���j
e = bb-9k�Cb(b�}6��k)�@�ib��0�Ck�͕������Ɍ���j >>6
���x�[�O�ϕ��\�ł����[�}���ϕ��\�Ƃ͌���� �uf�̒�ϕ��v�̓��[�}���ϕ��Ȃ낤��B
��������u���߂���v�̈Ӗ�����肩�ȁB
���ʂɍl�����
�u��������̍H�v�v�Ȃ�ėv��Ȃ����̂ȁB
����ꗝ�_���āA���w�̗��_�ł����
�A�C���V���^�C�������܂������Ȃ������A���̍l�����āA���ł��傤��
ℤ ��L�������Ƃ���.
Spec ℤ �� proper ���� smooth �� scheme �Ŕ��ȗ�͂���܂����H
ℤ ��̎ˉe���(P_Z)^n��,
ℤ �シ�ׂĂ̑f�_�ŕs����Ȑ�����O_K��̎ˉe���
�ȊO�̗��T���Ă��܂�.
�����ˁ[ �͏��W�Ƃ����܂��������
�l�b�N���X���Đ��쐔��Ȃ�ł����H���\����Ǝv����ł�����
>>10
y�Œ肵�ē������āA����x�Œ肵�ē������A�ʼn���
����ł���Ă� >>19
���W�͋敪�����܂��Ă���̂�����
���W�o�^���ꂽ��S���g���Ă����Ȃ��킯�ł͂Ȃ���
�����ˁ[�Ƃ������O�̕��[����o���Ă�������
�����ˁ[�Ƃ������O�̎����Ԃ��Ă����� ���Ƃ������p��ł܂��Ă���̂ł����A��낵�����肢���܂�
Z���ʑ���ԂƂ��ā@
Z is not reduced to a point
�Ƃ͂ǂ��������Ӗ��ł��傤���H
���肪�Ƃ��������܂�
��̓I�ɂ͂ǂ��������Ӗ��ł��傤���@���w�I�Ȓ�`�Ƃ�����
�����ŕς��܂����H
>>10
0<x<y �Ȃ̂ŁA�^����ό`�����
2{sin(y) -sin(x)}/(y-x) > sin(x)/x,
���ӂ�y�ɂ��ĒP������������
2{1 -sin(x)}/(��/2 -x) > sin(x)/x,
�Ȃ�Ώ\���B������
f(x) = 2x{1 -sin(x)} - (��/2 -x)sin(x),
�Ƃ�����
f(0) = 0�Cf(��/6) = 0,
f "(x) = (x +��/2)sin(x) -2cos(x) �� ��/3 -��3 < 0,�@�i��ɓ�)
���@f(x) > 0�@�@�i0<x<��/6) �킩��₷�������ĉ�����
9km���ꂽ�Ƃ���ɍs���̂ɁA�͂��߂� A km������6�L���ŁA�c�������4�L���ŕ����āA2���Ԃ��������BA�͂����炩�H
>>29
A/6 + (9-A)/4 = 2,
12�{����
2A + 3(9-A) = 24,
27 - A = 24,
A = 3, >>30
���肪�Ƃ��������܂����B �A�z�N��
115 ���O�F����P�~�X�g����[] ���e���F2018/04/01(��) 03:44:27.94
�]�k�����ǖ^�ł�
���o�o�A������N���q�}����
�����o�Ă����Ƃ��낾
����Ȃ���N���ĒN���������c
�����ł�����n�̏������݂�������
�܂��A�ł��A���̍ő�̖ړI�́A���嗝�w�����w�Ȃɓ��邱�ƂȂł͂Ȃ��āA
�u���v�ɂȂ��Ă�����x�Ɓu�L�v�ɂȂ�Ȃ����ƂȂB
�ǂ��������������ł���̂��H
�N���������������B
LN�̈ʒu�x�N�g�������߂�Ƃ������ŁA�ʒu�x�N�g���̌����H���g�킸����������̂ł����A(�摜2�A3���ڂł�)�������Ă���ł����Ă܂��ł��傤���H
�܂��A�ʒu�x�N�g���̌����͂͂�߂Ɋo�������������̂ł��傤���H



�����Ƃ����̂́A���Ԃ�ߖ邽�߂ɂ����ł�
������Ȃ��v�Z�ɗ]�v�Ȏ��Ԃ��₷�������ł������ƏI��点�����������ł����
>>37
�������̂͊ԈႢ�ł͂Ȃ�
�����_�H�̈ʒu�x�N�g���̌����������悤�ȕ��@�ŋ��܂�̂�����
�撣���Ċo����悤�Ȃ��̂ł͂Ȃ��̂ł�
ON��=OA��+t AB��
= OA�� +t (OB�� - OA��)
= (1-t)OA�� +t OB��
�̂悤�� �����̏ؖ��́A�����̖{����m��K�v������l�ȊO����Ȃ����
����Ȃ��͂Ȃ��ł���
�����ŏؖ��ł���A���Ȃ��Ƃ����̎菇��m���Ă���A�Ƃ������Ƃ͑厖�ł����A���������ԗւ̍Ĕ������J��Ԃ��K�v�͂Ȃ����낤�Ƃ������Ƃł�
>>39
�����܂���A���_���Ɛ}�I�ɂ����킩��̂ł����A�����_�Ȃǂ̈ʒu�x�N�g���͕��s�l�ӌ`���ǂ�����Ďg���ċ��߂�悢�̂ł��傤���H
���_�ȊO�̈ʒu�x�N�g���ɂ����s�l�ӌ`�g����ꍇ������܂�����A�����Ăق����ł�



>>42
�l�ɓǂ܂������Ȃ�A�������Ȃ�ɂ����J�ɏ�����A�S�~���I a(n,k)=nCk�Ƃ����B
���̂Ƃ��A�ȉ��̖���̐^�U�肹��B
�ua(n^2,k^2)=f(a(n,k))�ƂȂ鐮��f(x)�����݂���v
>>10
y=��/2 �Ő��藧�ĂA
�@2{1-sin(x)}/(��/2 -x) > sin(x)/x,�@�@�@�@>>28
�@x/sin(x) > (��/2 +x)/2,
�Ȃ�Ώ\���B������
�@g(x) = x/sin(x),
�Ƃ����B
�bx�b<��/2�@�� g(x) �͉��ɓʁB�@�@�@�@�c (*)
g(��/6)=��/3 �� g(��/2)=��/2 ��ʂ銄�����g���B
�@z = (��/2 +x)/2,
-��/2 < x < ��/6�@�̂Ƃ��@g(x) > (��/2 +x)/2,
(*)
1-cos(x) �� 0,
x-sin(x) = ��[0�Cx] {1-cos(t)} dt > 0�@�ix>0)
sin(x)-x�cos(x) = ��[0�Cx] t�sin(t) dt > 0�@(0<x<4.4934094579�j
���
g '(x) = {sin(x)-x�cos(x)}/sin(x)^2,
g "(x) = {1-cos(x)}/sin(x)�Eg '(x) + {1+cos(x)}{x-sin(x)}/sin(x)^3 > 0, p�������̒萔�Ƃ��A����an��a1=p,a(n+1)=an-r�Œ�߂�B
y=e^(-x)sinx
p�𐳂̎����̒萔�Ƃ��A0<r≤1/k�Ȃ鐳�̎���r�Ɛ�����n�ɑ�����a(n,r)��
a(1,r)=p,a(n+1,r)=an-r
�Œ�߂�B
������k�͐������̒萔�ł���B
xy���ʏ�̋Ȑ�C:y=e^(-x)sinx�ƁA����Dn:y=an�̌�_�̌���bn�Ƃ����Ƃ��Abn���ő�Ƃ���r�͈̔͂�p�̎��ŕ\���B
>>49
y = e^(-x) sin(x) ���
y ' = e^(-x) {cos(x)-sin(x)} = e^(-x) (��2) sin(��/4 -x),
x_m = ��/4 + m��@�ŋɒl y_m = e^(-x_m) (-1)^m�Esin(��/4) = C�{- e^(-��)}^m ���Ƃ�B
�im�������̂Ƃ��ɑ�Am����̂Ƃ��ɏ��j
������ C = e^(-��/4)/��2 = 0.322396942�c
�@����@-e^(-��) = -0.04321391826377�c
���āA�ǂ����邩�c {a1}=1/2, (n+1){an}=(n-1){a(n-1)}�Œ�܂鐔����B{an}��n�̎��ŕ\���B
�Ƃ������ŁA�ʉ��ɂ�����������킩��܂���
�2���Ƃ���ΐ����Ƃ�A
log(2,n+1)+log(2,{an})=log(2,n-1)+log(2,{a(n-1)})
{bn}=log(2,{an})�Ƃ����ƁA
{bn}-{b(n-1)}=log(2,[(n-1)/(n+1)])
����āA{b(n+1)}-{bn}=log(2,n/(n+2))
���̊K������^�̑Q��������A�܂�����{bn}�� ��ʍ������߁A{an}�̈�ʍ��������߂�
�ƁA�Ōオ�ȗ�����Ă���̂ł����A�ǂȂ��������Ă��������܂��ł��傤��
>>51
���ӂ����v�Z���銴����
(b2-b1)+(b3-b2)+(b4-b3)+...=
���Ă���Ă݂�Ǝ��X�ɍ��������� ��Ԃ�2�̉~
yz���ʂ̉~C:y^2+z^2=4
xy���ʂ̉~D:(x+1)^2+y^2=1
������B
���ʃ�t:y=2t(0≤t≤1)��y���Ƃ̌�_��T�A��t��C�̋��L�_�����ꂼ��P,Q�APQ�����a��T�𒆐S�Ƃ���~��Et�Ƃ���B������t=1�̏ꍇ�AEt�͓_N(0,2,0)�ł���Ƃ���B
A(0,0,2)����AD�̎���̓_L�AEt�̎���̓_M�A���o�R���ē_N�Ɏ���܂��ALMN�̒����̎�肤��l�͈̔͂����߂�B
ABC�\�z�̈Ӗ���������܂���
a�{b��c�����݂��ɑf�Ȏ��R��a.b.c�j�c�C�e�A�C�ӂ̃Á�0�ɑ���c��rad(abc)^(1�{��)�������̂͗L���������݂��Ȃ�
rab(abc)��1���傫���Ȃ�Ǝv���܂��������1�{�Ï悷��ƃÂ�����l�ȏ�ł���ΐ��c�ȏ�ɂȂ�܂���?
�����ł�
�Â͂߂����Ꮼ���������Ƃ����Ӗ��̋L���Ȃ̂ł����ˁH
�~�@�u�C�ӂ̃Á�0�ɑ���c��rad(abc)^(1�{��)�v�������̂͗L���������݂��Ȃ�
���@�C�ӂ̃Á�0�ɑ��āuc��rad(abc)^(1�{��)�������̂͗L���������݂��Ȃ��v
>>51
�@(n+1)n�a_n = n(n-1)�a_{n-1} = �c = 2�1�a_1 (=1)
2���Ƃ���ΐ����Ƃ�A
�@log{2�C(n+1)n} + b_n = log{2�Cn(n-1)} + b_{n-1} = �c = 1 + b_1 (=0) >>53
���ꌆ��Ȃ�ʼn����Ă������� �l�Ԃ��{��Ɏx�z����Ă��鎞�Ɏv�������Ԑ��͂V�ł���Ƃ����B
����𐔊w�I�ɏؖ�����ق��@�����ށB
�l�Ԃ̃e���|�����[�L��������b�ɂ��Ă��ǂ��B
>>53
���߂�
���̎�̖��͌��\�K��������Ƃ����Ӗ��ŊȒP�Ȗ��Ǝv���B ��`��ƒl�����萸���ɐ����ǂ������邾���ʼn����Ă��܂����B
>>60
�����@�����ł͏�肭�s�����A���ʐ}�`�̍l�@��������K�v������A���_�͈̔͂��ӊO��������܂� >>62
�킩���Ă�����������ɏ����̂̓X���`���낤
�悻�ł�� >>62
�N�������@�g�p����Ȃ�Ĉꌾ�������ĂȂ�
������x��������`��ƒl����Ɉ����ΕK�������Ă��܂���� >>64
�K�������Ă��܂����ǁA�܂������ĂȂ�����A�����������������Ă� Sn(m)��m��n��p���ĕ\��
S0(m)=1�ASn(m)=��S(n-1)(k) �yk=1�Am�z
>>67
�m��ˁ[��
�A�[�@�ł�����Ă� >>47 (*)
f(x) = sin(x)/x �Ƃ����ƁA
0 < x <�� �� f(x) > 0�Cf '(x) = {x�cos(x�j- sin(x)}/xx < 0,
�bx�b< 2.081575977818 �Ł@f "(x) = {(2-xx)sin(x) - 2x�cos(x)}/x^3 < 0,
�� ���ɂ��A
�@g(x) = x/sin(x)�Cg '(x) > 0�Cg "(x) > 0,
�k���l
f(x�jg(x) = 1�Ȃ��
�@f '(x�jg '(x) < 0,
����� f(x�jf "(x) < 0 �̂Ƃ�
�@f "(x�jg "(x) < 0,
(����)
�@g '(x) = -f '(x)/f(x)^2,
�@g "(x) = {-f(x�jf "(x) + 2f '(x�jf '(x)}/f(x)^3, >>67
S_n�im) = C�in+m-1�Cn) = (n+m-1)!/{n! (m-1)!}
S_{n-1}(k) = �b�in+k-2�Cn-1) = C�in+k-1�Cn) - �b�in+k-2�Cn)�@�@�@(k��2)
S_{n-1}(1) = �b�in-1�Cn-1) = 1,
k=1�`m �ł����B 3�����̓_P�̐ڐ��ɓ_P�Ō����@����3�����Əd���ɂȂ�悤�ȓ����3�����͂���܂����ˁH
���A�_P�ŏd���ɂȂ�3�����ł�
�@�����d���ɂȂ�Ƃ��������Ƃ�̂��A���݂�
�`�����V���K�X�X�ł��B
a1=2, n>=2�ŁAan���ȉ��̑Q�����̂Ƃ��A����{an}�̋Ɍ������߂�B

��@�͂͂��݂����Ȃ�ł����A�͂��݂������Q�����̕ό`�ɂ��ċ����ĉ������B
�Q�����Ȃ̂ŁAan+1 = an = x �Ƃ����Ă����āAx=1, 1/4 �ƂȂ�܂����A
�ł͕ό`���ꂽ����
an - 1 = 3/2 (��(an-1) - 1)
�ƂȂ��Ă��܂����A���̕ό`�̎d���̍������킩��܂���B
��ʓI�ȉ������ł́A�����������ŏo���Q�̉����A�����g���āA
an - �� = ��(an-1 - ��)
�Ƃ����悤�Ȍ`�ɂȂ�̂ł͂Ȃ���ł��傤���H
1/4�͂ǂ��ɍs�����́H�Ȃ��W��3/2�����̂܂g���́H
���Ȃ݂ɁA���[�g�����邩��Ƃ����ė��ӂ̒ꂪ�Q�̑ΐ����Ƃ��Ă����܂��ł��܂���ˁB�B
>>74
a_1=1/8 ��������ǂ��Ȃ邩���l���Ă݂�Ƃ悢��������Ȃ��B�B ���̌`�̑Q�����̈�ʍ��������I�Ȏ��ŕ\�����Ƃ͂ł��܂����H
>>78
1/8���Ƃ���ƁH�킩��܂���(�L�G�ցG`)
�U���̑O��ŁAa_n > 1 ���킩���Ă����Ԃł��B
��ʍ����o���K�v�͂Ȃ��i�Ƃ������A���Z�͈̔͂ł͏o���Ȃ��j
���ǁA�ŏ��̑Q�����̕ό`�ɂǂ�����Ă����Ă����̂����킩��Ȃ��̂ł��B
�Q���������ǁA
a_n - �� = ��(a_n-1 - ���j
�Ƃ͕ʂ̃p�^�[���ł���ˁB����͂ǂ������p�^�[���Ȃ�ł����H >>80
�Q�����̕ό`�̍l�����������Ƃ�
�w�ǎv�l�̗���ŁA��������Ȃ�����C���X�^���g�Ɏg�������ł͂Ȃ��Ǝv���Ƃ���
�E���̑Q������an����������Ƃ�����Aan��an-1�������l�ɂȂ�Ƃ݂Ȃ���
�E�Ă��ƂŁAan=an-1=t�Ƃ����đ������ƁA
t=(3/2)��t-1
2t^2-3t+1=0
t=1,1/2
�E��蕶���an��1���傫���̂ŁA��������Ƃ�����1�����Ȃ��B�Ȃ��Ȃ�1/2�Ɏ�������Ɖ��肷��ƁA���傫��n�̎���an��1/2�ɋɂ߂ċ߂��Ȃ�������Ȃ�����B
�E����ċɌ��l�Ƃ���1�����\�����Ȃ����Ƃ͕��������B
�����ŗ��ӂ���1�������Ă�邱�ƂŁA�Ɍ��l��0�ɂł���`������B����ɂ���ĕs�����̕]���⎮�̑��삪���₷���Ȃ�B�ȏ�B
���Ȃ݂ɂ���͂ǂ̃p�^�[���ɂ��g����l�����ł͂Ȃ��B
�Ⴆ�ΐ���a1=1,a(n+1)=an+(1/n!)��e-1�Ɏ������邪�A�Q��������ė��ӂ���e-1�������Ă���������͉̂����Ȃ�
�����܂Łu���[�g�̓������^�C�v�̑Q�����̋Ɍ��̍U���@�v�� >>80
���̃^�C�v�́u�����Ȃ��Q�����v�Ƃ��Q�l���ɏ����Ă��邯�ǁA��w�s���Ε����邪�Q�����Ȃ�Ċ�{�I�ɉ����Ȃ����̂���B
���Z���w�͂��̒��́u�����Ȃ�������Q�����v�ɂ��ĕ����Ă�킯�B������Q�����ɑ��Ă��܂����ό`���ł���ꍇ�͋ɂ߂Č����Ă�Ǝv���Ă����B
����������Ȃ����ǁA�u�Ɍ������߂₷���悤�ɕό`�ł��邾���A�\���Ƀ}�V�v�ȑQ�������Ǝv���Ă����Ƃ���
�Ⴆ���̑Q�����Ȃ�ĉ�����C���Ȃ��ł���B
an+1=sin(an)+an+3 >>80
�p�^�[���Ƃ��n���Ȃ��ƌ����Ă邪����Ȃ��̂Ȃ���B ������4/3�Ƃ������Ƃ͋��̑̐�(4/3)��r^3�̓��ł���(��)
�Ƃ������Ƃ�1��B
���ar�̋�B1������B
���̋�B1�ɑ̐ς��ő�ɂȂ�悤�ɉ~��A����ڂ�����B
����ɁA�~��A���ɑ̐ς��ő�ɂȂ�悤�ɋ�B2����ڂ�����B
�~��A����B1���œ������Ƃ��A
��B2�̒ʉ߂�����̈�̑̐ς͋�B1�S�̂̑̐ς�20%���傫�����H
>>80
> ���ǁA�ŏ��̑Q�����̕ό`�ɂǂ�����Ă����Ă����̂����킩��Ȃ��̂ł��B
�܊p�����l�̌��1���݂������̂�����A���ӂ���1�������ā@a_n - 1 ������Ă݂�A�Ȃ�Ĕ��z�͏o�Ă��Ȃ��̂��ȁH
��������@a_n - 1 = 3/2 (��(a_(n-1)) - 1) �͎��R�ɓ������B >>84
������B��26%�ɂȂ�B
�~��A�́A��~���a(2��2/3)r�A����(4/3)r�ɂȂ�B
��B2�́A���S����B1�̒��S����{(2��3-3)/3}r�A
���a��{(2��3-2)/3}r�ƂȂ�BB2���|���}�`�́A
B1�Ɠ������S�������A���a{(4��3-5)/3}r�̋��B
���̑̐ς�B1�̑̐ς�(164��3-845)/27��0.26�ɂȂ�B ����_�Ɋւ���
���̓_�ɂ�����@��=���̓_�ɂ�����ڐ�
�����藧�Ƃ������Ƃ͍l�����邾�낤���H
���ꂪ���̎咣�Ȃ̂ł����������������Ȃ�3����������ƕ������̂ł��̂悤��3���������݂���̂ł͂Ȃ����Ǝv�����₵�܂���
�L�q�̎��ɖ@���͂��̓_�ŏd���������Ƃ͖����Ƃ��ėǂ��̂��ǂ����̊m�F����������
�������g�ƒ��p�Ɍ����Ȑ��łȂ�A
���̌�_�ɂ����Đڐ��ł���A�����̓_�ɂ����Ė@���ƂȂ钼�����l���邱�Ƃ͂ł���ȁB
�Ȑ��̕���Ƃ������̂�B���ɏ�������̘b�����B
>>87
�ڃx�N�g���ۖ@�x�N�g��//�@�����ڐ�//�ڃx�N�g��
���Ȃ킿 �ڃx�N�g���ېڃx�N�g�� �ƂȂ�悤��
�ڃx�N�g���͑��݂����Ȃ�����ǁA
�Ȑ����A�����_�Ő����Ɏ��Ȍ�������悢�̂ł́H
�����j�X�P�[�g�̌��_�Ƃ��ˁB ���₷���̓s���ł����ł͕��f��w�̋��f����w'�Ə���
�i���j
���f���̒萔�Ƃ���B
���f��z�ɂ��Ă̕�����
��(|z|+i)z+|��|(|z'+i|-��)z'=0
�������B
�������Ƌ������ŕ\�킵�ĘA���������ɂ���
>>91
���̕��j�ł͍���ł���
���f���̂܂܂ŕ��f�����ʂ̐��������ĉ����Ȃ��ł��傤�� >>92
��Βl�L�����͂ޔ͈͂�A�J�b�R�̈ʒu�A�v���X�}�C�i�X�̕����A�����L���̕t���Y�ꓙ��
�ʂ��ԈႢ�͂Ȃ��ˁH >>92
�� =�b���be^(ib)�C
z =�bz�be^(i��),
�Ƃ����ƁA
�bz '+ ��| =�bz - ��| = ��(�bz|^2 -2|z�bsin�� +1),
�Ȃ̂�
�i�bz�b+ ��)e^(2��i) + |z - ���be^(-bi) - |��| = 0,
���`��
>>93
�@>>90 �̂P�s�ڂ��� ||z|e^(-i��)+i|=-(|z|+i)e^(2i��+ib)+|��|e^(ib) �ƂȂ邩�痼�ӂ��������
|z|=(|��|sin(b)-cos(2��+b))/sin(2��+b) ��������
�����O�̎��ɑ������Ƃ����߂鎮�ɂȂ邯�lj�͓I�ɉ����͖̂������ۂ�
���l�v�Z�Ȃ�ǂ��ɂł��Ȃ邪
>>90
���̖��̎ʐ^���A�b�v�ł��܂����H �X���`�C���Ȃ̎���
���l�v�Z��@�̈�ł���A��@���ėz��@�Ƃǂ��Ⴄ�낤�H�܂������������i�܂�
�A��@�ł̎��X�e�b�v�̏�Ԃ��v�Z����ɂ͗z��@�ƈ���Ď��X�e�b�v�ł̒l���܂܂�Ă�W�ōs��̕������H�������Ȃ���Ȃ�Ȃ��炵�����ǁA���̕������œ����l���ǂ������Ɍ��т��Ă����̂����킩��Ȃ�
(�ŏI�I�ɂ�C����̃v���O�����ɗ��Ƃ����݂����B�z��@�̃v���O�����͂�������Ă����ő����Ȃ�Ƃ����p�ł���Ɗy�Ȃ��ǂ����ȒP�ɂ͂������ˁH)
���̉������ł����v�ł��傤���H





�������͂������ǁA�ꍇ�����R�ꂪ�����p��g���������������
�������ꂢ�Ȃ̂́�
>>102
�������̌�0�̎�(0<a<1)�̂Ƃ������������������ł���
�����
2t-1�Ŋ���悤�Ȏ��ό`����Ȃ�At=1/2�Ƃ���ȊO�Ƃŏꍇ�킯����悤�ɏ��������������ł���
���̓I�b�P�[�łӂ��H �����������ǂ��ł͂Ȃ��āA�����Ȃ��Ƒ啝���_�̉\������
�ut=1/2�̂Ƃ��͂킩��܂���ł��������v �ƁA�ut=1/2���ؗ�ɃX���[�v�̍��͂ł���
���ʕϐ��������Č�������101�̕����̎d��f(t)=a���w���Ǝv�����ǂȂ�
�m���ɉ����邵
����A�����o�ŁH
�����o�ł́A�ϐ���������Ƃ��Ɂu�O���t�Ō��₷���`�ɂ�������v���ĕ��j������
�Œ肳�ꂽ�Q�����ƁA��_��ʂ钼���̑g�ݍ��킹�ɂ킯�邱�Ƃ͑��������͂��B
���������ȒP�Ȏ��𐄏����Ă��悤�ȁE�E�E
���̕ӂ͗Ջ@���ςɉ����₷�����@��I�ׂ����Ǝv����
�Q�l���͐�III���w�K���Ă��Ȃ��l�ɂ��z�����ď����Ă���낤
������III�m���ĂĂ�����̕��@�̕����y�������莎����ł��ꂵ���v���t���Ȃ��Ȃ�g��Ȃ����R�͂Ȃ����A������������
>>103�Ŏ����Ō����Ă�ʂ�t=1/2�����C��t����Ζ��Ȃ��Ǝv�� ������̋�Ԃ������̖�����̖�����̖�����̖�����́E�E�E�E�i���ꂪ�����̖������
������̖�����́E�E�E�E�i���ꂪ�����̖�����̖�����̖�����̖������
��������ǂ�Ȋ����ɂȂ�̂ł��傤���H
�܂��A����炪�����̖�����̖�����̖�����̖�����́E�E�E�E�E�i���ꂪ�����̖������
������̖�������j�����œ�������ǂ�Ȋ����ɂȂ�̂ł��傤���H
�_����ɂ͂ǂ�����Ηǂ��ł����H
���̂悤�Ȏl�ʑ�ABCD�͑��݂��邩�B
�E��BC�̒��_��L�ACD�̒��_��M�ADA�̒��_��N�Ƃ���Ƃ��AAL��BC�ABM��CD�ABN��DA
�E��ABM�͐��O�p�`
��ӂ̒�����k�ŁA���̕ӂ̒��������ׂ�1�ł���l�ʑ�V������B�ȉ��̖₢�ɓ�����A�Ȃ��ݖ�i1�j�Ɓi2�j�Ƃ̊Ԃɒ��ړI�Ȋ֘A�͂Ȃ��B
�i1�j����k�̎�肤��l�͈̔͂����߂�B
�i2�j�ȉ��̏������݂������ʃ������Ȃ��Ƃ�1���݂��邱�Ƃ��������B���Ȃ킿�A���ɂ��蕪����ꂽ2�̗��̂������ł��邱�Ƃ��ڂ�����������B
�uV�����Ő�ƁA�蕪�����Ăł���2�̗��̂������ɂȂ�v
>>113
BM��CD�@���@BC = BD > BM
�@2���ӎO�p�`BCD�̓��ӂ́A����BM��蒷���B
BN��DA�@���@BD=AB
��ABM�͐��O�p�`���@AB=BM
����@BD = BM
�����͖�������B
���S�ʑ�ABCD�͑��݂��Ȃ��B �R�C���������P�O�O�����ĂR�A���ŕ\���o�������߂�ɂ́A�ǂ��J�E���g����悢�̂ł��傤��
123�A456����ƃJ�E���g����99��܂ŁH98�A99�A100�ƂR�A���\�̏ꍇ�́H
>>118
�x�N�g���Ōv�Z���悤�Ƃ��Ă킯���킩��Ȃ��Ȃ����̂ł����A���ʐ}�`�ł���ȂɊȌ��ɉ�����̂ł��ˁB
���肪�Ƃ��������܂��B ��s����m,n��p���� 3m+5n=x �ŕ\���Ȃ�1�ȏ�̎��R��x��S�ċ��߂�
����������
8,9,10 ��\�����Ƃ��ł���̂�11�ȏ��x��8,9,10�����ꂩ�̂Ƃ���m�̒l��ς��邱�Ƃō���̂�7�ȉ���x�ɂ��čl����
7�ȉ���x�� 3�̔{���A5�̔{����S�ď����� x=1,2,4,7���c�肱���͑S��3m+5n=x �ł͕\���Ȃ��̂ŋ��߂�x��
x=1,2,4,7
�Ƃ���������(�����ԏȂ��Ă܂���)��������ł����͎���̂Ƃ����������ł����v�Ȃ�ł����ˁH
�͔͉Ƃ܂������Ⴄ�����Ȃ̂ŕs���ɂȂ�܂���
�ꉞ8,9,10��\��m,n�̑g����̓I�ɒ��āA���n�Œ��m�̂ݓ������A3�Ŋ��������̗]�肪0,1,2��8�ȏ�̐������ׂĂ�\����̂ŁA�����8�ȏシ�ׂĂ̐������s�������B
���ď����āA���Ƃ͎����̓��Ăő��v�ł����ˁH
>>122
�����Ǝv����
���邳�����ƌ����A1�A2�A4�A7��5m+3n�̌`�ŕ\����Ȃ����Ƃ��������K�v�����邩�����Ċ����B ��8,9,10 ��\�����Ƃ��ł���̂�11�ȏ��x��8,9,10�����ꂩ�̂Ƃ���m�̒l��ς��邱�Ƃō���̂�7�ȉ���x�ɂ��čl����
m��1�An��1�A�ł͂Ȃ�����A����Ȏ��͌����Ȃ��B
a��b���݂��ɑf�̎��Aab�{1�ȏ�̑S�Ă̎��R���́A
ax�{by(x�Ay�͎��R��)�̌`�ŕ\�������o����B
����̏ؖ��́A�m���Ă��鎖�ł͂��邪�A�ȉ��̂悤�ɂȂ�B
n��ab�{1�������R��n�ɑ��āAn�|a�An�|2a�A�d�d�d�An�|ba�A���A
b�Ŋ������]��͑S�ĈقȂ�B
�]���āA���b�̎��R���̒��ŁAb�Ŋ�������̂�����B
����� n�|xa�Ƃ���ƁA�����yb(y�͎��R��)�̌`�ŕ\�����B
�܂�An�|xa��yb �� xa�{yb ��n
������A�g�̐����h�Ɍ��肷��ƁAab�{1�ȏ�̑S�Ă̎��R�� ��
ab�{1�|a�|b��(a�|1)(b�|1)�ɕς��B
�܂�A(a�|1)(b�|1)�ȏ�̐����͑S�āAax�{by(x�Ay�͔̐���)�̌`�ŕ\�����B
�]���āA(3�|1)(5�|1)��8������A�������m���߂鎖�ɂȂ�B
�E����7�̎��A����3m+5n�A�ł͕\���Ȃ��B
�E����6�̎��A(���A��)��(2�A0)�ł���Ηǂ��B
�E����5�̎��A(���A��)��(0�A1)�ł���Ηǂ��B
�E����4�̎��A����3m+5n�A�ł͕\���Ȃ��B
�E����3�̎��A(���A��)��(1�A0)�ł���Ηǂ��B
�E����2�̎��A����3m+5n�A�ł͕\���Ȃ��B
�E����1�̎��A����3m+5n�A�ł͕\���Ȃ��B
�ȏォ��A����1�A2�A4�A7.
>>122
�ނ��낱����̕������R�ȉ��Ǝv��
���̖͎��̉͗]����g���ĕ��ނ��Ă�̂��� �����͔͉��m��A
n=0,1,2 �ł���Ă݂��ق���������Ȃ��́H
>>115
k = AD �Ƃ���B
��ABC �� ��BCD �͕Ӓ��P�̐��O�p�`�B
BC��AD �䂦 AD��y���ABC��z�� �Ƃ��Ă悢�B
A�i��(3-kk�j/2�C-k/2�C0)
B�i0�C0�C-1/2)
C�i0�C0�C1/2)
D�i��(3-kk�j/2�Ck/2�C0)
�ƕ\�킹��B
(1)�@0 < k < ��3
(2)�@x���i��AOD�̂Q�������j�̎����180߉Ώd�Ȃ荇���B�i2�j
�@�@�� =�ix�����܂ޔC�ӂ̕��ʁj ���aa�̉~A�Ɣ��ar�̉~B���_P�ɂ����ĊO�ڂ��Ă���B
2�~�̋��ʐڐ��̂����AP��ʂ���̂�l�AP��ʂ�Ȃ����̂�1��m�Ƃ����B
�ȉ��̖₢�ɓ�����B
�i1�jm��A,B�Ƃ̋��L�_�����ꂼ��S,T�A�܂�l��m�̌�_��U�Ƃ���BU��ST�̒��_�ł��邱�Ƃ������B
�i2�jm�A�~A�A�~B�ň͂܂��̈�̖ʐς�Sr�Ƃ����B�Ɍ�
lim[r��0] Sr/(US�EUT)
�����߂�B
���肢���܂��B
(0,0)�A(89,492)��ʂ�Ay=tan70��x+247�ƌ����A���S��y���W��0�̉~�͑��݂��邩�H���݂���ꍇ�A���̉~�̔��a�͂����炩�H
>>130
(0,0)�A(89,492)��ʂ�A���S��y���W��0�̉~�Ƃ����̂͂P�ʂ肵���Ȃ�
��������߂ď����ɍ��������ׂ�Ƃ����̂ł́H �u���v�ɂȂ��Ă�����x�Ɓu�L�v�ɂȂ肽���Ȃ��̂ł����A�ǂ��������������ł��܂����H
>>130
�~�̕������͊ȒP�ɏo��
���ɌX����tan70����s�����ŕ]�����āA�s�����̉����Ə���̏ꍇ�̒������m���ɉ~��ʂ邱�Ƃ��m�F���A���Ԓl�̒藝 >>132
�z�ɖ����}�W�b�N�Łu���v���ď����Ƃ� >>135
�^�ʖڂɋ����Ă��������B���肢���܂��B >>129
������Ȃ��̂ł��肢���܂�
m�Ɠ�~�ň͂܂ꂽ�����̖ʐς����߂�ꂸ�A�s�����ŕ]�����ł��܂���
�Ɍ����v�Z������@�������Ă������� ��x^2+y^2+z^2=4�ʃ�:y=-��3�Ő������̂́A���W�̌��_O���܂ޑ���C�Ƃ���B
���ɂ�鋅�̐ؒf�ʂł���~�̒��S��P�A�_(0,0,2)��Q�Ƃ���B
C��PQ�̎���Ɉ��]�����Ăł��闧�̂̑̐ς����߂�B
k�𐳂̐����Ap��0��p<2k+1�Ȃ鐮���Ƃ���B
����{an}���A
a1=k^2+p�Aa(n+1)=[��an]-1
�ƒ�߂�B
������[x]��x���Ȃ��ő�̐�����\���B
�i1�jan�͌�������ł��邱�Ƃ������B�@�i2�jan���͂��߂�0�ɂȂ�n��k��p�ŕ\���B
>>129
�K���ɑ����g��k������ a = 1 �Ƃ��Ă悢
�~A �̒��S�� A �Ƃ��ā@��ASU = �Ɓ@�Ƃ���
SU �� r �� �ʐς� �� �̎��ŕ\���� �����E�������g���ĉ�����2-3���Ŋ��o�I�ɂ�50�x���ȂƂ͎v�����ǐ����o���Ȃ��́c

>>141
�Ⴄ��B
BD�̒��_��M�Ƃ���ƁAM�́�ABD�̊O�S��
AM=
��AMD= >>142
���`�cAM=AC=6�̓ӎO�p�`��X=40�x�ł����B
�ł�����͍����E�����̖��Ȃ�ł������̉������ł����̂��Ȃ��c? arctan1/3+arctan1/9
tan��1=1/3, tan��2=1/9
��=��1+��2
tan��=(tan��1+tan��2)/(1-tan��1tan��2)=(1/3+1/9)/(1-1/27)=6/13
��=arctan(6/13)
����ŊԈ���Ă܂���
>>130
>>131 �ɏ]���A�i0�C0�j��ʂ�~�̎���
(x-r)^2 + y^2 = r^2,
�Ƃ���B
��ӂ��_�i89�C492�j��ʂ邩��
r = (89�89+492�492)/(2�89) = 249985/178 = 1404.410112359550
�����@-y�cos(70�) + x�sin(70�) + 247�cos(70�) = 0
�Ɖ~�̒��S (r�C0) �̋�����
�@0 + r�sin(70�) + 247cos(70�) = 1404.192794542818 < r
�䂦�����͌����B
��_��
(x�Cy) = (76.450742287334�C457.046688134994)
�@�@�@ = (93.350268046508�C503.477753557818) >>143 �i�ʉ��j
�����藝��
�@AD/sin(��B) = BD,
�@AD/sin(x) = AC/sin(��ADC),
���
�@sin(x) = (AD/AC)sin(��ADC)
�@= (BD/AC)sin(��B)sin(��DAB+��B)
�@= 2sin(��B)sin(90�+��B)�@�i�� BD/AC =2�C��DAB=90�)
�@= 2sin(��B)cos(��B)
�@= sin(2��B),
�� x = 2��B, >>146
���肪�Ƃ��������܂�
������2�̍����E�����̒P���Ȃ̂ł��̉ł͂Ȃ��Ǝv���܂� cos��+isin��=e^i�Ƃ��ē�������肭���ݍ��߂Ȃ�
�}�N���[�����W�J���Ĕ�r���Ă����ؖ��̗���͕��������
���ɕ��f�����ʏ�̓_��re^i�Ƃŕ\���鎖���[�������Ȃ��Ƃ������Ȃ�Ƃ�����
�ǂ�����ė�����������H
�}�N���[�����W�J�]�X�̃��x���ɓ��B���Ă��Ȃ��Ƃ������Ƃł�
�����������A�ƒ��߂܂��傤
>>148
cos�Ƃ�sin�Ƃ̓ƂłQ�K��������ƌW��-1���o��-cos�Ƃ�-sin�ƂɂȂ�
e^i�Ƃ��Q�K���������-e^i�ƂɂȂ�
�����������������y"+y=0�̉��Ȃ̂ŁA�������݂��̐��`�����ŕ\�����Ƃ��ł���A�ƍl����ƒ����I�ɂ͗������₷���̂ł͂� ���_���������Ă��Ȃ��Ƃ��������̘b
>>141
>>142�̕��j��AM=BM�������������������ŏؖ������炢���̂ł� �p�����[�^�Ƃ����ƕ��f���ʁixy���ʂ��Ƃ݂Ȃ��j��̋Ȑ����łĂ���Ƃ��������ǁA���ꂪ�ǂ������ӂ��ɂȂ邩�l�����
�������Ă݂�Ǝw�����Ȃ̂ŌW����i ����������i e^i�ƂɂȂ�
����́Axy���ʂł͐i�s������90�x�����������̂ł���A���ꂪ�A�i�s������
�����͂ƂȂ�
�܂�A��ɐi�s�����Ɛ����ȓ��ʂ̗͂�����葱����^���ɂȂ�̂Ŋ�Ղ͉~
��`��
�����I�ɂ͂���ȂƂ���
���f���ʂ��ėv��Ȃ��ˁ[�H
���݂��Ȃ���
���݂�����W���ʂƍ��W��Ԃ����ʼn����ł��邾��
>>153
�������킩��Ȃ��Ȃ疳������K�v�͂Ȃ��ł��� >>154
���W���ʂ����Ď��݂��܂���
���Ȃ��̐g�̉���x���͗����Ă܂����� >>148
���ݍ��ޕK�v���[������K�v���Ȃ�
�ؖ���������Ώ[�� >>156
���܁A���̏������Ă݂���x���������Ă���ł����c >>162
�悭����B����͍��H�����ٓ��̊��蔢���B ���̑̂ɂ�sex axis���t���Ă邯�ǂȁI
HAHAHA
>>148
�@���z(��)�����̒�`��f���Ɋg������ہA���ڒ��ɂ���Ă��܂��ƁA�uz�Ŕ�������v�����ł����s�ցB
�����ŁA�܂Ñ������A�L�����Łi�C�ӂ̐��x�܂Łj�ߎ����i�}�N���[�����W�J�A���[�����W�J�j�A����f�����ă�����Ƃ������@�����B
��������L�����͎l�����Z�����Ȃ̂ŁA���f���͗e�Ղł���B >>162
�ɂ����I�@�u��v���ז��� >>148
������Ae^x �f���������̂�����2��i�����A�Ȃ�Ă��Ƃ͑z�����ł��Ȃ��B�i������g���������Ă��邯��ǁj >>165
�@������z�̑������A�L�����Łi�C�ӂɁj�ߎ��ł���A�Ƃ����Ӗ��Łu�������ɏ����鈵�����\�v�Ɗ��҂����B
�@������u�����v�Ə̂��āA����ȊO�̏ꍇ�ɂ͖ڂ��҂�̂��ӂ��B �����̉҂��āA�����̒m���Ђ��炩�����߂Ɏ���ɊW�Ȃ����Ƃ܂Ő��ꗬ����ł���
���̎���҂��āA�����̒m�����Ђ��炩�����߂ɏ��X�̖�������������Ə̂��ď����Ȃ����Ă��ł���
������Ȃ����������X���Ɏ���̖�����\��A�������Ȃ��Ȃ�܂ł͌���Ȃ���ˁH
��1���x���̖��Ő\����Ȃ��̂ł���
�Q����3x-�Q����3x����0�ł���ˁH
���W�̉���3x�Ȃ̂ł������������킩��܂���
>>172
���̎ʐ^���A�b�v���[�h�ł��܂����H >>156
�ԓ��ɂ͐Ԃ����������Ă�炵�� �q�킶��Ȃ����炢���������l���A������w���w�����w�Ȃ�ڎw���͖̂��d�ɂ��قǂ�����܂����H
���Ȃ��Ƃ��q�}��������͖������Ǝv���܂�
�q�킶��Ȃ����炢���������Ȃ�a�C���낤�����҂Ɍ��Ă��炢�Ȃ���
�f�@������؋��Ƌ��ɂ�����ɕ��Ȃ���
����������₢�ɓ����悤
0����a����180���Ƃ���B
tana���Etan(a��+10��)�Etan(a��+20��)=tan(a��+30��)
�ƂȂ�a�����ׂċ��߂�B
p��f���Ƃ��Axy���ʏ�̑o�Ȑ��̈ꕔC:x^2-py^2=1�ix>0�j���l����B
�i1�jC��̊i�q�_�ŁA(1,0)�ȊO�̂��̂͑��݂��邩�B
�i2�jC��̓_�ŁA����i�q�_�Ƃ̋���h��0<h<0.001�ƂȂ���̂����݂��邱�Ƃ������B
�i3�j�i2�j�̊i�q�_�̋�̗��1������B
�S�Ă̖ʂ������Ȏl�ʑ�V������B
V�̊e���_���炻�̑ΖʂɌ��������������낵���Ƃ��A�����̂����Ō������̂��������Ƃ����B
���̂Ƃ��AV�͐��l�ʑ̂ł��邱�Ƃ������B
178�`180�͂ǂ�����ł�
������������
�����܂���A7.14��3.4���������܂���B
���������Ăǂ�������ł��������H(�L�E�ցE�M)
1)�o�C�g������
2)��������������A����ւ���
3)�d���
>>180
�܂��l�ʑ̂̊e�ʂ��O�p�`�ł��鎖������
�l�ʑ̂����l�ʑ̂̐��^�ϊ��ŕ\���鎖������
���Ƃ͌v�Z >>181
�܂����ł��邱�Ƃ��ؖ����Ă��� �q�}�������ĂȂ�Łu�q�}�����v���Ė��O�Ȃ́H
��ԍ����Ƃ���ɓo�肽���Ƃ��������畨���̏Z�l�����Â���
>>180
���̖��͌��삾�Ǝv���̂ł����A�Ȃ��N�������Ȃ��̂ł����H �悭�l�����瓖����O���������܂�
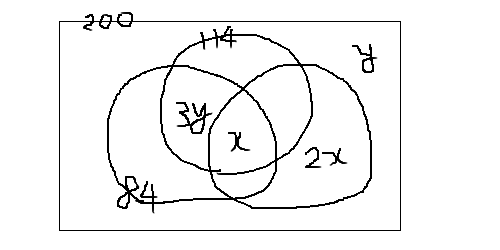
���W��Ԃɒu���ꂽ���ʏ�ɂ́A���W�̐�xyz���ő�ɂ���_�����Ȃ��Ƃ�1���݂���B���̂��Ƃ��ؖ�����B
2p(p+1)=q(q+1)����������p,q�ɂ���p�̉��ꌅ��S�ċ��߂�
���X���ɂ��������lj��������S�R�v������
>>175
�킴�킴������w���w���ɐi�w���Ƃ��Ċ����Đ��w�Ȃ�I�ڂ��Ȃ�Đl�́A
����Ӗ��q�킶��Ȃ��قǓ�����������A�s���������悤�Ȓ��Ԃ������B
�S�z�Ȃ����B >>187
�J�X�e������������A�r㻕������i�v���y���A�\�ʂ̍��������X��
�\���Ƃ����Ă���ȁB�l�����̂́A���{�َ̉q�����������B �V�x���A�A���܂ɐH�ׂ����Ȃ��
���a1�̉~C�ɓ��ڂ��鐳�O�p�`�ƁAC�ɓ��ڂ���s�p�O�p�`������A���̋��ʕ����̖ʐς�1/8�ł���Ƃ����B
���̉s�p�O�p�`�̖ʐςƂ��čl������l�͈̔͂����߂�B
>>197
����͂ǂ������Ӗ��ł����H �i1�jy�𐳂̎����Ƃ���Ƃ��A0��yx^2+yx��1�ƂȂ����x�͈̔͂����߂�B
�i2�jz�𐳂̎����Ƃ���Ƃ��A
0��xz^2+2z��1�ƂȂ����x�͈̔͂����߂�B
�i3�jxyz��Ԃɂ�����
0��yx^2+yx��1 ���� 0��xz^2+2z��1 ���� 0��y ���� 0��z
���������̑̐ς����߂�B
�S�Ă̖ʂ������ȎO�p�`����Ȃ�l�ʑ�ABCD������A���̊e�ʂ�3�ӂ̒�����4,5,6�̎O�p�`�ł���B
AB��1:2�ɓ�������_��P�AAC�̒��_��Q�ACD�̒��_��R�Ƃ���Ƃ��A���̎l�ʑ̂�3�_P,Q,R��ʂ镽�ʂŐ�������̐}�`�̖ʐς����߂�B
������AB=6�AAC=4�Ƃ���B
���l�ʑ̂̊e���_���_P������AP�͎���0�ł͓_A�ɂ���B
P�͎���n(n=0,1,2,...)�ɂ����Ċm��p�ŗאڂ���_�Ɉړ����邩�A�m��1-p�Ŏ���n-1�ɂ����_�ɗ��܂�B
����k(k=0,1,2...)�ɂ����āA�_P���͂��߂đS�Ă̓_�ɓ��B����m�������߂�B
�������������3��u���Ă����܂����B
�s��ϕ����ł��܂���B�����Ă��������B
��1/��{(1-2ux+u^2)(1-2vx+v^2)}dx
�_�l�Ȃ烊�[�}���\�z�Ȃǂ̒�������u�ʼn�����Ƃ������A
���ɑS�Ă̂����邱�Ƃ̓�����m���Ă���̂ł��傤���H
�z�_�I�ؖ��s�\����͐_�l�ł�����m��Ȃ�
�S�m�S�\�̐_�l�Ȃ�A���R�A�z�_�I�ؖ��s�\����̓������m���Ă���̂ł͂Ȃ��ł��傤���H
���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��̂ł����A���E�����Ă����ʂł����H
���ʂȂ낤��
���̒��q�ō����������̓���������
>>215
�A���v�X�̕����悩�������A�q�}����
335 ���O�F����k�ł��傤�H���������� [sage]�F 2012/01/12(��) 12:04:04.36 ID:???
���{�̎R�ł��肢���܂��B
���̐�����[���R�ł��肢���܂��B >>217
���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��ł��B
����ł������I�ɂ͖��ɂ͂Ȃ�Ȃ��炵���ł����A���_�I�ɂ͖��ɂȂ��̂ł��傤���H ���߂̌����͉��ߎҎ��g�̌Œ�ϔO�B���߂̎��R�ɂ͐ӔC������
���t���I�����̗���͂���������l�̐S�̗���̎��ȓ��e�B�l�͋�
���{�͈ꎞ�̋��C�A���m���\�̎��ȏؖ��B���r���[�Ȓm����قnj��V
�u�^���͈�v�͍���B��������҂قǖ�����̌��i�����ϔY�j
���l�ɕs���R�i����j��^����ΌȂ��s���R�i�s���j��
�������̖͂R�����҂قǎ��Ȗh�q�ׂ̈ɗ�V��@�}�i�[��v��
��͗͂̒Ⴂ�҂قǃf�}�@���t�F�C�N�^���Ȋw�Ɋ������]
���ȍm�芴�̌������҂قǁu�Ȃ̒m�������S�Ő^�v�Ɏ��ȓ���
�l���o���̏��Ȃ��҂قnj����L���C�|���E�U�C�����z��O��̌�
�L���X�g���͐��E�ő�̃J���g�B�����͎j��ł�����Ă���g�{
�S�Ă͕K�R�B���R ��� ���s�s �s�𗝂͎v�l��~ ���싷��̎Y��
�l�������ۂɌ��X�Ӗ����l���R�ړI�`���g���͂Ȃ�
�@�������̓y�n���͑����́u�����v�ł͂Ȃ��u�������@����v
�s�ߍ��ʔƍ߃e�������͍���\�B�K�v�Ȃ͓̂K�؏\���ȍ��x����
�̔��͎w���͖������̖͂R��������f�l�̓ƑP�Â��Ӗ��ӔC�]��
���Y�͖��x�̒Ⴂ�r���I�W�c�����`�E�l�B�u���˂Ώ�����v�͋U�P
�j�����_�͐l�ԕs�M�Ɨ��ɉՂ܂ꂽ���a�ȊO��f�l�̐��_�����
���[���ቺ�͎Љ�n�̒���B��l�ϐl�̓��I�͋c�����ߑ��̏؍�
����ȐӔC�_ �`�w�Z�ł͋����Ȃ�������`�N�w�`�@m9�M��֥)
>>218
�����̊p�ɓ����Ԃ��Č��� ���̃X�����čr�炵�̑��A�Ȃ̂��H
���̈������ɓV�˕����w�����肢���܂��B
���̖�肪������܂���B
�r���܂łł���̂ł����ǂ����Ă��Ō�̋l�߂��ł��܂���B
��낵�����肢���܂��B
���
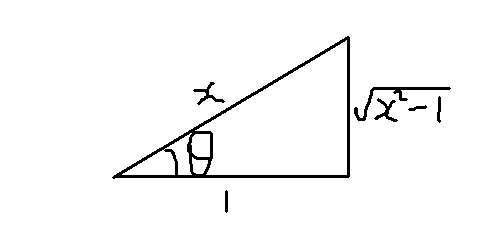
tan(Sec^-1 x) ���������
�ڂ����r���v�Z�����肢���܂��B
x��sec�Ɓ�1/cos��
tan�Ɓ�sin��/cos�Ɓ���(1�|cos^2��)/cos�Ɓ�x��(1�|1/x^2)����(x^2�|1)
>>233
������
X/��(X^2-1) �炵��
����
d/dx*sec^-1�}1/(x*��(x^2-1))
������
d/dx*Sec^-1 x=1/(x*��(x^2-1))
�r���܂łł������ǁE�E�E
y=tan(Sec^-1 x) �Ƃ���
u=Sec^-1 x �Ƃ���
du/dx=1/(x*��(x^2-1))
dy/du=(tan u)'=1/cos^2 u=sec^2 u
dy/dx=dy/du*du/dx=sec^2(Sec^-1 x)/(x*��(x^2-1))
��������ł��܂���B >>235
����csec^2(sec^-1 x)=(sec(sec^-1 x))^2=x^2����Ȃ��́H �� = Sec^{-1} (x) ��� x = sec�� = 1/cos��
>>235
�ԈႢ
��d/dx*sec^-1�}1/(x*��(x^2-1))
d/dx*sec^-1=�}1/(x*��(x^2-1)) �� = Sec^{-1} (x) �Ƃ����� y = tan(Sec^{-1} (x)) = tan��
y�f= 1/(cos��)^2 �E����/dx = x^2 �E 1/(x ��(x^2 + 1)) = x/��(x^2 + 1)
>>239
�Ȃ�قǁE�E�E
���肪�Ƃ��������܂��B�i�O�O�j �W���ɂ��Ă̘a�Ƃ���
�@C(n,r) �~ C(n+1,r) �� r=0 ���� n �܂ł̘a
�͌v�Z����ɂ͂ǂ���������ł����B
�����ꂪ���w�̎��͂ł�
���Ȃ̂Ɉُ�Ƀ��x�����Ⴂ
�����������w�̏����ł��鍂�Z�����x��
C(2n+1, n) ���ȁB
(1 + x)^n = �[k=0, n] C(n, k) x^(n-k)
(1 + x)^(n+1) = �[l=0, n+1] C(n+1, l) x^l
������A�ӁX������
(1 + x)^(2n+1)
= �[k=0, n] �[l=0, n+1] C(n, k) C(n+1, l) x^(n-k+l)
���̉E�ӂ��� x^n �̍��A
���� k = l ���݂��������o���ƁA
���̌W���� �[k=0, n] C(n, k) C(n+1, k) ������A
���ӂ� x^n �̌W������ C(n+1, k)
>>243
�I�}�G���i�[�i���������j >>244
�Ȃ�ł���ȃX�S�C�������łł����ł����I
���������ēV�˗l�ł����B f(x)=1�ix���L�����̂Ƃ��j�A1�ix���������̂Ƃ��j
�Ƃ������͘A���ƌ����܂����H
>>249
��`��͐ڑ��ł���̂ł����H �F����s�m��腖��剤�͂ǂ����̕��������̂ł��傤���H
>>251
��`��͎����S���ł���
f(x)=1�Ɠ����ł� 1���̓X���̃��W�A1���Ԃ�����40�l�̋q���K���̂ɑ������ł���l����1���ԂɃʐl�ł���
1.1���Ԃ�����ɐl�̋q�������ɖK��A�X����1���Ԃ�����ʐl�̏������\�ł���Ƃ����ł́A���������܂ߏ��i�����̂��߂�n�l�̋q���҂��Ă���m���͈ȉ��ł���
Pn=(1-��/��)(��/��)^n (n>=0)
���̂Ƃ���L�̎����m���ɂȂ邽�߂̃ʂ̏���������
2.����1�œ��������̉��A�ȉ��̊W�������Ƃ�����
��0���� Pn=1
3.��L�̕s���������ŏ��̃ʂ̒���5�̔{���ƂȂ�l�����߂�
4.�X��K�ꂽ�q���������J�n����܂ł̕��ώ���Wq��
Wq=(��/��)/{��(1-��/��)}
�ŗ^�����邱�Ƃ��m���Ă���A����2�ŋ��߂��ʂ̉��A���ώ��Ԃ͂ǂꂭ�炢�ɂȂ邩�A�P�ʂɂ��ĉ���
���a1�̉~C�ɓ��ڂ��鐳�O�p�`��ABC������B
�ȉ��̏��������ׂĖ������s�p�O�p�`�S�̂���Ȃ�W����S�Ƃ���B
�i1�j���a1�̉~C�ɓ��ڂ��Ă���B
�i2�j�~C���3�_A,B,C���A��ABC�����O�p�`���Ȃ��悤�ɓ������Ƃ��A��ABC�Ƃ̋��ʕ����̖ʐς�1/8�ƂȂ邱�Ƃ�����B
S�̗v�f�ł���s�p�O�p�`�̂����A2�Ԗڂɑ傫���Ȃ��ӂ̒�����L�Ƃ���Ƃ��AL�̂Ƃ肤��l�͈̔͂����߂�B
>241
��[r=0�Cn] C(n�Cr)�~C(n+1�Cn+1-r)
��
2n+1�̕��� n��(n+1)�ɕ����Ă��獇�v(n+1)�I�Ԃ���
2n+1�̕����� ���̂܂�(n+1)��I�ׂ�
C(2n+1�Cn+1) = C(2n+1�Cn)
>>257
nCk�EpCq=(n,k,p,q)�ƕ\���Ƃ��A
(a,b,c,d)=(a,e,c,f)
�ƂȂ�e,f�͉��ʂ肠�邩�B 9-4=5 ��5�̔{���ł���ˁH
���������
9��4 (mod 5)
���Ǝv����ł����A
9��5�Ŋ������]���4�ł�����
4��5�Ŋ���Ə���0.8�A�]��0
�ɂȂ��ŁA�������̒�`�ɔ�����Ǝv���̂ł����A
��������������ł��傤�H
>>178
a = 50 + 90n,
a = 55 + 90n,�@
(n�F�����j
>>210
�o1/��(uv)}log�b��{(1-2ux+uu)/u} + ��{(1-2vx+vv)/v}�b�@�c�@uv>0
-(1/u)��(1-2ux+uu)�@�@�@�@�c�@u��0�Cv=0
-(1/v)��(1-2vx+vv)�@�@�@�@�c�@u=0�Cv��0
x�@�@�@�c�@u=v=0 ���� ��x^2+3��x+��-1=0...(A) ���l����B
(A)���A���f���̒萔�Ƃ��āAx�̕������ƌ����ꍇ�̉����d�������߂ă��A���Ƃ���B
�܂�(A)���Ax�f���̒萔�Ƃ��āA���̕������ƌ����ꍇ�̉����Ƃ���B
���܂��̓��ƁA����v����Ƃ��́A�����������ׂ��������q�ׂ�B
���̍ۃ��f���̒萔�Ƃ��Ĉ�������B
>>261
��+�� = -3,
���� = (��-1)/��,
�� = 1/(xx+3x+1), �x�����n���g�E���[�}���Ɩ���T����͂ǂ����̕��������ǂ��ł����H
���w������̗͂�����܂���B�̗͂�����ɂ͂ǂ������炢���̂ł��傤���H
�ǂ����̘_����
���������݂����ނƂ������ď����Ă�������
�~����ɓ��Ԋu��7�_��ł��@�L��܂��H
�p�x�𐳊m�ɏo���Ƃ��ł͑ʖڂł��B
�~�̑傫���͓��Ԋu�ɑłĂ�̂ŗL��ǂ�ȑ傫���ɂ��Ă��ǂ����ɂ��܂��B
��낵�����肢���܂��B
>>268
������Ċp����12.54mm�܂�݂����Ȃ̂ł����H �`�Ƃa���A���l���Z�q�ł��s���i�`�j���s���i�a�j���P�@�@�i�ʎq�͊w�ł����Ƃ���̖��x���Z�q�j
���݂����s��ŁA����s��w�������āAY���w�G���~�[�g�����Ƃ���Ƃ��A
�`�@���@�w�a�x
�Ƃ����W�ɂ���Ƃ��Arank�i�`�j��rank(B)�@�����藧��
�Ƃ������悤�Ȏ咣���ؖ������ɖ{�ɏ����Ă������̂ł����A����͂ǂ�����Ď����̂ł��傤���H
�i�������������܂��������̂ŏ�����������Ƒ���Ȃ���������܂���B���݂܂���B�j
�O����M���[�M���[���邳���������������Ƃ����������͂����茾��
���X����B�������N��������Ȃ��悤�ɂ��Ȃ��ƒ��q�ɏ��Ȃ��̂��J�M�́B
�ڋ��ȃK�L�͖ق�B
>>274
������R���p�X�ƒ�K�����ł͍�}�ł��Ȃ��A�ƌ���Ă��� >>275
��}�o���Ȃ����̂̏ؖ����@���ĂȂ���H ���E�������ł�
�I�X�X���̎��E���@�������Ă�������
���������݂����ނƂ����炵����
�l�͍�}�ł�����@��T���Ă���ǁA
�Ⴆ�Ί������P�ʉ~���c�Ɖ��ɕ��ׂāi0.0�j(A.7A)�̌��_���Ȃ��ł����ƕ��s����������Ƃ��������ȁH
��}����~�����S�ɗ��邩�͋^�₾����...
>>281
���ꐳ���`����Ȃ��H
�s�^�S���X�ŃA�v���[�`�����ق����ǂ��Ǝv����B25:24:7�����܂��g����Ώo���Ȃ��͂Ȃ��Ǝv���� >>282
�Ⴆ����Ⴆ�B
�s�^�S���X���Ď���25�̉~��`���Ă����̂����H >>278
��������Ƃ��������ɂȂ邯�ǁA(�R���p�X�ƒ�K��)��}�\���͒P�ʒ�(������P�Ƃ���)�ɉ����揜�ƊJ��(������)�̑����L����{���Ăł��鐔�Ɍ�������̂ŁA
�����p�`�̏ꍇ�Az^7=1�ƂȂ�p��z�����߂���ŁA���̕�������㐔�I�ɉ������Ƃ���ƁA�ǂ����Ă��r���łR���������������K�v�������āA�R�捪�̑��삪�K�v�ɂȂ�̂ō�}�\���̏����������Ƃ��ł��Ȃ�
���Ċ���
�ŁA�R���p�X�ƒ�K�ł͕s�\�ƌ����Ă��鐳���p�`�̍�}���A�܂莆���g���Ɖ\�Ƃ���Ă���
��̓I�ȕ��@�͊o���Ă��Ȃ��̂Ńl�b�g�Œ��ׂ铙���Ăق����Ǝv�����ǁA�܂莆���g�����ł͂R���������̉�����}�\�ɂȂ邽�߁A���̂悤�Ȃ��Ƃ��ł���̂��Ƃ��B >>284
�Ȃ����肻���ȕ�����Ȃ��悤�Ȃ���
���s�^�S���X�̃A�v���[�`������݂��������ǂ���g���Ă����߂��� >>285
���߂�B25:24:7���g���ĉ������悤�Ƃ��Ă�̂��͐����킩��Ȃ��B
�ߎ��ł悯���tan(2��/7)��1.25�Ȃ̂ŁA�X��5/4�̒����������Ƃ�����ۂ��p�x�������Ȃ����ȁB
���������ۂ��ȊO�̉����ł��Ȃ����ǁc >>282
�ǂ������H
������2�l����グ���B�ڍ�] ���f���ʏ�̒P�ʉ~C����_P�̕\�����f��z�ɑ��A����z�̗L����w=f(z)���l����ƁAw=x+yi��y=x^2�����Ƃ����B���̂悤��f�ɑ��A�ȉ��̖�ɓ�����B
(1)f(z)�̗��1������B
(2)����f��I�ԁB���̋t����g�Az=g(w)�Ƃ����B�܂��Aw=x+yi��y=x^2���݂����Ƃ���i-��<x<+���j�B
���̂Ƃ��Af�̂Ƃ���ɂ�炸�A�_P(z)��C��̑S������B
>>289
�����A�T���N�X
A��B�������悤�ɒJ�܂�ɂ���̂��~�\�Ȃ낤�Ȃ��Ă��Ƃ͂킩�� ���w�������Ȃ��ǁA���w�ɋ���������Ƃ����l��������w���w�����w�Ȃ�ڎw���Ƃ����̂͂���ς��߂Ă����������ǂ��̂ł��傤���H
50��ŗ�������Đ��w��U�Ńh�N�^�[�܂ōs���ĉ��ɂȂ�H
����A��50�ザ��Ȃ����E�E�E�E�E�E�B
����A��50�ザ��Ȃ����E�E�E�E�E�E�B
Rotman��An Introduction to Homological Algebra�Ƃ����{�̑�1��1�߂ŁA�z�����W�[�̋N���́A�����`���̐ϕ���path�̓Ɨ������l����Ƃ���ɂ���ƌ����悤�Ȃ��Ƃ�������Ă���̂ł����A����̓|�A���J���ȑO�̘b�ł��傤���H
���w���S�ɖY��Ă܂��B
�u�������v�u�W�J�v�u�����v�ł����Ƃ������Ă݂����Ǖ�����Ȃ��̂ł��ɂȐl�v�Z�ߒ��i�������j�������������I�I
�������@����0.1�@�̑O��ŁA�����u111.9 = 1000x + 1100x^2 + 900x^3�v�̂Ƃ��@�� ^ �ׂ͂���̂���
��������ǂ��W�J�H�����H������ x��0.1 ���o���Ă����̂���������Ȃ��̂ł��B
����͕������ł���
x=0.1������Ɗm���ɃC�R�[�������藧���Ƃ��킩��܂�����A���ꂪ�����ł�
���ߕ��͊��ł�
�u�Y��Ă�v���ǂ��܂Ŏv���o���郌�x�����ɂ���邪�c
�ڍ�����10�{�����
9000x^3+11000x^2+10000x-1119=0
�ƂȂ�A�������������
(10x-1)(900x^2+1190x+1119)=0
������900x^2+1190x+1119=0�͎������������Ȃ��̂�
���������Ƃ�������������Ȃ��
10x-1=0 �� x=0.1
�܂��A����ł͏��X���\�Ȃ̂ŁA�������ʂ����悭���邽�߂�t=10x�Ƃł�������
9t^3+110t^2+1000t-1119=0
�ƂȂ�A���ӂ�t=1����������0�ɂȂ�̂͂����C�����̂�
(t-1)(9t^2+119t+1119)=0
�ƈ�����������̂͂��قǓ���Ȃ��B
���w��Y��Ă�l���A�Ȃ����́u�����̕������Ă���R���������v��
������x���w�I�ɉ��������K�v���������̂��ɋ���������B
>>300�@������Ȃ����@������Βm�肽���ł��B�ł����w�̐��w�̕��� x^2 �����������H����Ƃ��Ɋ��݂����Ȍ`�ŁA
�@�@�@�@�����ł��낤����������œ��č���Ő������o�����ꂢ�v���o���v���o���܂����E�E�E�B
>>301�@���������肪�����ł��I�I�������@(10x-1)(900x^2+1190x+1119)=0�@�œ��H�ȏ�Ԃł����A�Ƃ肠�������������ł������Ă݂܂��B
�@�@�@�@�ۑ�ŎЍ@�����@�@���q���̌v�Z�e�L�X�g�������Ă���̂ł����A299�ŏ����������炢���Ȃ萳���� 0.1 �Əo�Ă��āA
�@�@�@�@�Ȃ�Łi�ǂ�����āj 0.1 �o�Ă�낤�Ǝv���܂��āB���Z���w�Ŋ��ɗ�������������Ԃł����B �l�ʑ�V�̊e�ӂ̒��_��P,Q,R,S,T,U�Ƃ���B
����6�_�̂���1�_X���Œ肷��B�c��5�_�̂�������1�_Y���A������XY���ŏ��ƂȂ�悤�ɑI�ԁB�������_Y�̌�₪��������ꍇ�́A���̂����̂ǂ��I��ł��悢���̂Ƃ���B
���̂悤��X�Ƃ���P,Q,R,S,T,U��I�сA��L�̂悤�ȑ�����s�����Ƃ���A������̏ꍇ��XY�̒l���������Ȃ����B
���̂Ƃ��AV�͐��l�ʑ̂ł��邱�Ƃ��ؖ�����B
���Z���w�͑�w���w������鎞�ɂ͉��̖��ɂ������Ȃ��̂ł��傤���H
�W��2nCk=(2n,k)=ak�ɂ��Ĉȉ��̖₢�ɓ�����B
�i1�jak�̌�����bk�Ƃ���Bk=0,1,...,n-1�ɑ��A�s�����@bk<b(k+1)�@�����藧�悤��n�͈̔͂����߂�B
�i2�jn�́i1�j�̏��������Ƃ���Bk=1,2,...,n�ɑ��Aak���\�i�@�ŕ\�����Ƃ��A���̍ŏ�ʂ̌��̐���ck�Ƃ���Bck��c(k-1),c(k-2),...,c0�̂����K�v�Ȃ��̂�p���ĕ\�킹�B
���R��n�ɑ��A�ϕ�In��
��[0����] x(sinx)^n dx = In
�Ƃ����B
���̂Ƃ��A�Ɍ�
lim[n����] n^a�Eln
��0�łȂ��萔�Ɏ�������悤�ȗL����a�̒l�����߂�B
>>307
��[0�C2N��] x�osin(x)}^n dx
= ��[k=0�CN-1] ��[2k�C2(k+1)��] x�osin(x)}^n dx
= ��[k=0�CN-1] ��[0�C2��] (2k��+��) (sin��)^n d��
= ��[k=0�CN-1] (k a_n + b_n)
= N(N-1)/2 a_n + N b_n,
�����ɁA
a_n = 2��[0�C2��] (sin��)^n d��,
b_n = ��[0�C2��] �� (sin��)^n d��,
n�F�����̂Ƃ� a_n >0�Cb_n >0,
n�F��̂Ƃ� a_n =0�Cb_n <0,
������AN���� �Ƃ���Ɣ��U����B
��I_n �͑��݂��Ȃ��B >>308
a_n = 0�@(n:�)
�@�@= (2��)^2 (n-1)!! / n!!�@(n:����)
�X����F�c�쥈ꏼ�u���w����I�v��g�S��221 (1956) p.245 >>165
�uz�Ŕ����ł���v
�܂蕡�f�������ł���Ƃ́A
�ǂ̌������� z��a �ɋ߂Â��Ă�
�of(z)-f(a)}/(z-a) �������l�ɋ߂Â��A
�Ƃ������ƁB
�Ίp�ɒ��ڂ���Aarg{f(z)-f(a)} - arg(z-a) �� c,
�܂�_a�ɂ�����f���p�x��ۂ��ƁB�i���p�ʑ��j
�s��ϕ������k∲ f(z)dz = 0�l�Ȃ�ΐ����B�iMorera�̒藝�j
�܂��A�����Ƌ��������ꂼ�� Cauchy-Riemann�̎��������Ƃł�����B
����}�Ȋg���̗�iCauchy-Riemann�����Ȃ��j
�@z = x + i y �Ƃ���,
�@f~(x�Cy) = f(x) + y�og(x�Cy) + i�h(x�Cy)} >>310
�y�A�m�Z�p���܂ޔC�ӂ̖������Ȍ����n�ɑ��A���郂�f��M,N����ј_�����ӂ����݂��āAM|=�ӂ���N|���ӂƂł��邱�Ƃ������A�Ƃ�����肪�킩��܂��� >>311
���������p�C�i�b�v����H�ׂ��
�y�A�m�Z�p���܂ޔC�ӂ̖������Ȍ����n�ɑ��A���郂�f��M,N����ј_�����ӂ����݂��邱�ƂɂȂ�Ƃ����_��������炵����B
����ɉ����Ċ��������݂����ނ�M|=�ӂ���N|���ӂ������Ɏ������Ƃ��ł��� >>311�܂��ł����H
�m�������͂ł���̂�>>311�͂킩��Ȃ���ł��傤�� �傫�����������m�ȃx�N�g��A�Ƒ傫���ƕΊp�����m�ȃx�N�g��B�̍��ł���x�N�g��X�̑傫���͌v�Z�ł��܂����H
���V�ː��w�҂ƉF����s�m�͂ǂ����̕��������́H
�_���u�S�Ă͖����l�B�ŋ��⋆�ɂ⎊���Ȃ�ĂȂ��B�v�Ƃ����v�z�̕��������ł���ˁH
�_���u�S�Ă͖����l�B�ŋ��⋆�ɂ⎊���Ȃ�ĂȂ��B�v�Ƃ����v�z�̕��������ł���ˁH
�J���Ȃ��Ă�������
���u�`������H
����������
>>304
���ꌆ��Ȃ�ł����ǒN�������Ȃ���ł��� f(0)=777�ł��鐮��f(x)�ŁA�ȉ��̏����������̂͑��݂��邩
�wf(7^n)���\�i�@�\�L�����Ƃ��̑S�Ă̌��̐�����7�ɂȂ�悤������n�������ɑ��݂���x
>>324
���O�������������낤 n^3-1���������ɂȂ�Ȃ����Ƃ��ؖ�����
>>327
���ɂ͓���ĕ�����܂���B
���w�����ڝ��̂قǂ�낵�����肢�������܂� >>324 >>304
�U�̖���͏ؖ��ł��Ȃ�����B
����F��ʂ��P�ӂP�̐��O�p�`�C�R�̑��ʂ����������ӂP�ΕӂQ�̓ӎO�p�`�ł���O�p��
�ŁA�Ȃɂ���肽���́H >>332
���肪�Ƃ��������܂��B
���Ȃ��̂������Ŏ��͂���Ɉ�i���݂ւƓo�邱�Ƃ��ł��܂��� 335�P�R�Q�l�ڂ̑f������2018/04/12(��) 23:43:41.37
�@�@�@�@�@�@�@�@�@�@__�)-'�L�P�P`�- �_
�@�@�@�@�@�@�@ ,�@'�L�@�@_. -�]'''"��j�=-`�R�A
�@�@�@�@�@�@�^�@�@ �^:::::; -�]''"�@�@�@�@�@ �@ `��m
�@�@�@�@�@/�@�@�@�^:::::�^�@�@�@�@�@�@�@�@�@�@�@�_
�@�@�@�@ /�@ �@ /::::::/�@�@�@�@�@�@�@�@�@ |�@|�@|�@ |
�@�@�@�@ |�@�@�@|:::::/�@/�@�@�@�@�@|�@�@|�@|�@|�@|�@ |
�@ �@ �@ |�@�@�@|::/�@/�@/�@|�@�@| ||�@ |�@| ,� .| ,�|
�@ �@ �@ |�@�@�@|/�@/�@/�@/|�@,��|�@/|��,�|�'�@
�@�@�@�@ |�@�@�@|�@ |�@/�@/ �',��ځ� ,��|�/�@�@�@���͑��̐����^�ȂƂ͕t������Ȃ���B
.�@�@�@ �@|�@�@�@�_ �ڃC�@ ,��C|�@�@�@ ,`-' |�@�@�@�@�@�@�����ǂ��Đ��w���o���Ă����������l�B���ꂪ�K�v������B
�@�@�@�@ | �@�@�@�@l�O,�l| �@` `-' �@ �@ �T�@ |�@�@�@�@�@�@�@�@����� Ann.of Math �ɘ_�������Ώ\�������ɂ��Ȃ���B
�@ �@ �@ | �@�@�@�@ ` -'�_�@�@�@ �@ �@�' �@�l�@�@�@�@�@�@�@�@�@�@��Ԍ����Ȃ̂͘_�����𑝂₷���߂ɂ�����Ȃ��_����������
�@�@�@�@|�@�@�@�@�@�@�@ /(l �@�@ �@�Q�Q�^�@ �R�A�@�@�@�@�@�@�@�@�@�@�@�ǂ��_���̏o�ł�x�点�邨�n���Ȑl�B
�@�@ �@ |�@�@�@�@�@�@�@�i:::::`�]-�__ �@|::::`� �@ �@ ��ƁR�A�@�@�@�@�@�@�@�@�@���Ȃ��̘_���� Ann of Math �� accept �����m����?
�@ �@�@|�@�@�@�@�@�@�^ `�]-�::::::::::`�]-�::::�_�@�@ /,�Ƥ�_�@�@�@�@�@�@�@�@�@�@�@�@����Ƃ��ŋ߂� Inv. Math. �̕����ォ����H
�@�@�@|�@�@�@�@�@�@|::::::::::::::::::|` -�:::::::,́P|'��@ �Ɠ�A�@�_
.�@�@ |�@�@�@�@�@�@/::::::::::::::::::|::::::::�_/:::�n`�::�_ �@ |�@'��@�@ �_
�@�@ |�@�@�@�@�@ /:::::::::::::::::::/:::::::::::::::::::::::::::::'�::::�_Ɂ@�@�R�A�@ |
�@�@|�@�@�@�@�@ |:::::�^:::::::::/:::::::::::::::::::::::::::::::::::'�',::::'� �@/:�___/�]�
�@�@|�@�@�@�@�@ |�^:::::::::::/::::::::::::::::::::::::::::::::::�n::| '�::|�@��:::::::::::::�P|
�@�@ |�@�@�@�@ /_..-'�L�P`�-�:::::::::::::::::::::::::::::::::::|/:/`�]'::�_;;;;;;;�Q|
�@�@�@|�@�@�@�@|�^::::::::::::::::::::::�_:::::::::::::::::::::::::::::|::/::::|::::/:::::::::::/
�@�@�@ |�@�@�@/:::::::::::::::::::::::::::::::::|:::::::::::::::::::::�n::|::|::::::|:::::::::::::::/
�������u���������v�̈��������E�E�E�B
���������A���N���N����������肾����폟�Ȃ�ˁE�E�E�B
���܂ɂ́A�����Ȃ������Ȃ����ƔY��ŕ����Ă݂����A���ꂪ���̐؎��ȔY�݁B
����{an}�͂ǂ�k���̑������ς�����Ă�1�ł���Ƃ����B
�i1�j{an}���L������̂Ƃ��A�C�ӂ�i,j�ɑ���ai=aj�ƌ����邩�B
�i2�j��������̏ꍇ�͂ǂ����B
2�̑�A��B������A�܂��ʂƐԋʂ��\���Ȍ��p�ӂ���Ă���B�����ɑ��A�ȉ��̂悤�ȑ�����s���B�����ꂪ�s����m����������1/4�ł���B
�E��A�ɐʂ�����
�E��B�ɐʂ�����
�E��A�ɐԋʂ�����
�E��B�ɐԋʂ�����
���̑�����J��Ԃ��A�܂̒��̐ʂ̌��Ɛԋʂ̌��������ɂȂ����Ƃ��A�܂̒��̋ʂ�S�ĊO�ɏo����ɂ���B�������܂���̏ꍇ�́A�ʂƐԋʂ̌����Ƃ݂͂Ȃ��Ȃ��B
���̑����n��s�����Ƃ��ɑ�A,B�Ƃ���ł���m��pn�����߂�B������n��1�Ƃ���B
�L����p�͏z�߂̒�����3�A�L����q�͏z�߂̒�����4�ł���B
p+q�̏z�߂̒����Ƃ��Ă��蓾�鐮���̒l��S�ċ��߂�Bp+q�������ƂȂ�ꍇ�͏z�߂̒�����0�Ƃ���B
�u�S�Ă͖����l�B�ŋ��⋆�ɂ⎊���Ȃ�ĂȂ��B�v�Ƃ����v�z�ɏ�����͖̂����ł����H
�Ƃ�����������悤�Ǝv�������A
��������ƁA���̎v�z�ɉ��l������Ƃ������ƂɂȂ��ɁA
�ŋ��⋆�ɂ⎊��������Ƃ������ƂɂȂ��Ă��܂��̂��E�E�E�E�B
����ȁE�E�E�E�B
�_�������ōŋ��ł�
�Y�ނ��Ƃ͂���܂����
>>330
���ɂ�����̂Ŏw���ł��܂���B����̂���������҂��Ă���܂��B �_���u���ɂȂ��Ă�����x�ƗL�ɂȂ�Ȃ��v�̕��������ł���ˁH
��Ζ����̑傫���̊ϑ��҂������Ƃ�����A���̊ϑ��҂Ɍ����鐢�E�́A
2�����炸�̑傫���̊ϑ��҂Ƃ͉����������Ⴂ�܂���ˁH
�_�̑傫���͂ǂ̂��炢�Ȃ̂ł��傤���H
�_���u���ɂȂ��Ă�����x�ƗL�ɂȂ�Ȃ��v�̕��������ł���ˁH
>>349
�����̎���X����A���Ő��������Ƃ�����Ă������� ���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��B
>>340
���O�����������Ƃ��Ă�
�����Ɛ}��������Ȃ����挩�Đ�����
�N�Y���남�O�H
���Ԃ̘Q����������
�ዅ�j�� ���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��B
�u�S�v���S�i�v���ōU����������ǂ��Ȃ�܂����H
���A������A�����A����A�ǂ�������NG�ɂ���q�}������NG�ɂł���
x�͂Q���̎��R���ŁAx��4�C6�C13�Ŋ������Ƃ��̗]�������a�Ab�Ac�Ƃ���Bb��a�̓�{��c��b�̓�{�ɂȂ�Ƃ����B���̂Ƃ��Ax��5�Ŋ������Ƃ��̗]��͂����炩�H
������1,2,3,4,0�̂����P��
�h�肷�B�����͂킩��܂ւ�B��������̂�
>>360
LCM(4�C6�C13) = 156
��ӂ��A(a�Cb�Cc) = (a�C2a�C4a)�@�@0��a<3
�Ea = 0 �̂Ƃ�
�@x �� 0�@(mod 156)
�Ea = 1 �̂Ƃ�
�@x����̂Ƃ��� b��2
�@x�������̂Ƃ��� a��1
�@�� ���Ȃ�
�Ea = 2 �̂Ƃ�
�@x �� 34�@(mod 156)
x��5�Ŋ���Ɓc >>362
>M�͕�AB�̐^�̓_�ł�
�E�E�E���̂����D�D�D a=b=c=0����2���̎��R���͂Ȃ�
0<b=2a<6���(a,b,c)=(1,2,4),(2,4,8)����
4k+1=6l+2�͗��ӂ̋��قȂ�(1,2,4)�͕s�K
10��4k+2=6l+4=13m+8��99
m�͋�����2n�Ƃ�����26n+8
34,60,86�̂���34�̂ݓK
>>337
����oa_n�p�̘A������k���̑������ς�1�ł���Ƃ����B
���̂Ƃ��A�C�ӂ�i�Cj�ɑ��� a_i = a_j �ƌ����邩�H
>>339
p = m/999�Cq = n/9999�@�Ƃ�����B(m�Cn�͐����j
1/999 = 1/(10^3 - 1) = (10^6 + 1)(10^3 + 1)/(10^12 - 1) = 1111*900991/(10^12 -1)
1/9999 = 1/(10^4 - 1) = (10^8 + 10^4 + 1)/(10^12 - 1) = 111*900991/(10^12 -1) >>337
����oa_n�p�̘A������k���̑������ς�1�ł���Ƃ����B
���̂Ƃ��A�C�ӂ�n�ɑ��� a_{n+k} = a_n �ƌ����邩�H 2^(��2)���������ł��邱�Ƃ͏ؖ�����Ă��܂����H
���l�ʑ̂���̕��ʂŐ�Ƃ��A���̒f�ʐς��ő�ɂ��������������B
p,q�݂͌��ɑf�Ȏ��R���Ƃ��A����{a[n]}��
a[1]=1,a[2]=1
a[n+2]=p(a[n+1])+q(a[n])
�Œ�߂�B
���̂Ƃ��ǂ̂悤�ɑf��p��I��ł��Aa[1],a[2],a[3]...�̒��ɁA�K��p�Ŋ����鍀�����݂��邱�Ƃ��ؖ�����B
>>370
����:
�f��p���f��P
p�Ŋ����遨P�Ŋ����� >>370
����͍����̎v���̌�������ł����A�ؖ�����������Ă���܂���B
��ɂ��m�b�����݂����������܂� >>372
���̎c�O�Ȋ����X���̎�̂������ȁH >>364
���_�A���藝���Ă̂���������Y��Ă܂����I�I
���肪�Ƃ��������܂��� p(a[n+1]),q(a[n])���ǂ��������Z���Ӗ����Ă���̂��܂������킩��Ȃ�
���߂ɒf����Ă����܂����A���͕ʂ̃X���Řb��ɂȂ��Ă���l���ł͂���܂���B
�ȉ��̌v�Z�E���_�̂ǂ�������Ă��邩�����Ă��������܂��B
�������j�̒��œ������Ƃ�������l�͂���͂��ŁA�ǂ������Ԉ���Ă���̂ł����c
�P�Ȃ�v�Z�~�X�ł���A�\����܂���B
http://fast-uploader.com/file/7079177251543/ �����܂���A���ȉ������܂����B
�n�����Ȃ��c
�l�ʑ�V�ɂ��āA���̊e�ӂ̒��_�S�Ă�ʂ鋅B�����݂���Ƃ����B
����ɂǂ̂悤�ȏ����������AV�͐��l�ʑ̂ƂȂ邩�B
�ȉ�����K�v���\���ȏ����̑g�ݍ��킹��I�ׁB
���̂悤�ȑg�ݍ��킹����������ꍇ�́A�����S�Ă���B
�i1�jV�̊O�ڋ��̒��S��B�̒��S�ƈ�v����B
�i2�jV�̓��ڋ��̒��S��B�̒��S�ƈ�v����B
�i3�jV�̏d�SG��B�̒��S�ƈ�v����B
�i4�j5�ӂ̒��������ꂼ�ꓙ�����B
�i5�j4�ӂ̒��������ꂼ�ꓙ�����B
�i6�j3�ӂ̒��������ꂼ�ꓙ�����B
>>369
���ʂɌ������鐳�l�ʑ̖̂ʂƌ��������Œ肵�A���̏����ł̍ő�ʐς��l����Ηǂ� f(x)=(x+1)exp(x)�Ag(x)=(x^2+1)exp(-x^2)�ɑ��A�ϕ�
��[0����] g(x)/f(x) dx
�����߂�B
>>370
a[1] = a[2] = 1�@��
a[n+2] �� q�a[n]�@�@(mod P)
���
a[2k+1] �� a[2k+2] �� q^k�@(mod P)
P�Cq ���݂��ɑf�Ȃ�@q^k �� 0�@(mod P)
�䂦�AP�Ŋ����鍀�͂Ȃ��B �ŋߑ��l�̂̕����n�߂����̂ł�
�����`���̑S�̂̓R�z�����W�[�_�Ȃǂł悭���܂����A�x�N�g����̑S�̂͊���̉��Q�ɂȂ�ɂ��ւ�炸�g���Ă���̂��������Ƃ�����܂���
�x�N�g����̑S�̂͂ǂ̂悤�ȂƂ���Ɏg����̂ł��傤��
>>151
���_��������Η����ł���́H >>382
�N�����̐ϕ��������Ă��������B
5�����ʎq��ɂ�����r���������̈�ʉ��ƂȂ蓾�܂� �_�ƑS�͂ǂ����̕��������ł����H
�_�͑S�Ɋ܂܂�邩��S�̕��������ˁH
�_�͐��E�̑n����ł�����_�̕����������ł�
�_�͐��E�̑n����ƌ����Ă��A���̐_���S�Ɋ܂܂��킯������A�S�̕��������ˁH
����@������͂���Ƃǂ��Ȃ�܂����H
�v�l�͂��d������V���ʈꎟ�����̖��ł�
����a,b,c�ɑ���x�̕�����ax^2+bx+c=0�̉��ɂ��āA���B�͊w�K�����B
�i1�j���̎��̍��ӂ�ό`���邱�ƂŁA���̕������̉����Ȃ����B���i�A�j�ɁA�ߒ��������ď����Ȃ����B
�i2�j�ȉ��̋߂Ȃ����B
(a,b,c)=(2,6,1)�̂Ƃ��A���̕������̉������i�C�j�Ɍ��ʂ̂ݏ����Ȃ����B
�ȉ��A(a,b,c)�����ꂼ��ꌅ�̐������Ƃ���B
�i3�j���̕��������������������Ȃ�(a,b,c)�����g���邩�����i�E�j�ɁA�ߒ��������ď����Ȃ����B
�i4�j���̕��������������������A��������cx^2+bx+a=0�������������悤��(a,b,c)�̑g��S�ċ��߁A���i�G�j�ɉߒ��������ď����Ȃ����B
���E��������n���ɗ�����̂��ȁH
1�`99�̐�����33����3�̑g�ɕ�����B
�ǂ̂悤�ȑg���������Ă��A���ꂼ��̑g����1���v3�̐������o����
���̂���2�̐��̘a���c��1�Ɠ������Ȃ�悤�ɂł��邱�Ƃ������B
����Ȃ��ƌ�����̂ł���
>>404
(1)
�@a��0 �̂Ƃ��A���ӂ� 4a ���|���� (2ax+b)^2 - (bb-4ac) = 0,
�@bb -4ac ��0 �̂Ƃ��A2ax+b = ��(bb-4ac)�Cx = {-b�}��(bb-4ac)}/(2a),
�@bb -4ac <0 �̂Ƃ��A�������Ȃ��B
�@a=0�Cb��0 �̂Ƃ��Ax = -c/b,
�@a=b=0�Cc��0 �̂Ƃ��A���Ȃ��B
�@a=b=c=0 �̂Ƃ��A���ׂĂ�x
(2)
�@(-3�}��7)/2,
(3)
�@bb-4ac <0
�@b=1,�@9�~9 = 81
�@b=2,�@81- 1 = 80�@ (1,2,1)
�@b=3,�@81- 3 = 78�@ (1,3,1) (1,3,2) (2,3,1)
�@b=4,�@81- 8 = 73
�@b=5,�@81-14 = 67
�@b=6,�@81-23 = 58
�@b=7,�@81-29 = 52
�@b=8,�@81-36 = 45
�@b=9,�@81-42 = 39
�@�v 573�B >>412
�_����͂��邱�Ƃ͂ł��܂��� >>403
����@���i���FMahāvairocana�j�́A�^�������̋���ł��镧�ł���A�����̖{���B
��̏�����F�̖{�n�B
���{�̐_���K���̉��߂ł́A�V�Ƒ�_�i���孁�M�j�Ɠ��ꎋ�������B �_�ɍ��G�l���M�[���q���Ԃ��܂�
1.�ǂ̖ʂ̖ʐς�������
2.�ǂ�2�̖ʂ������łȂ�
����2�̐��������l�ʑ�OABC�����݂��邱�Ƃ��ؖ��������Ǝv���Ă��܂��B
���j�Ƃ��čl���Ă���̂͒��Ԓl�̒藝���g�����@�ł��B���������ł���
�u��CAB=��OAB�ƂȂ�悤��4�_OABC���Œ肷��B
��CAB���ʂɌŒ肵�āA��OAB��AB�����Ƃ��Ē�ʂ����]������B���������Ďl�ʑ�OABC�̑̐ς�0����傫���Ȃ��Ă������A���̓r���Ł�OBC=��CAB�ƂȂ邱�Ƃ������B
����ɁA���̏����̂��ƂŁ�OBC=��OAB�ƂȂ�悤��OABC�����邱�Ƃ������v
�������Ō�́u���̏����̂��ƂŁ�OBC=��OAB�ƂȂ�悤��OABC������v�������܂���B
���Ԓl�̒藝���g�����@�ł͑ʖڂł��傤���B���������������B
������X�̕��Ք핢��Ԃ�X�̊�{�Q�Ŋ�������Ԃ�X�Ɠ����ɂȂ邱�Ƃ̏ؖ��������ĉ�����
�_�╧�͐��w�z���Ă���̂ł��傤���H
�w�Z�̏h��ŏo�܂������肢���܂��E�E�E�i�P�j�̓����i���|���j�^�i���|�P�j�ł��邱�ƈȊO
�S�R������Ȃ��ł��������B(TOT)
�قȂ邎�̒n�_�i�����Q�j���ړ����邠�鐶��������B���̐����͖��b���C�O�����n�_�Ƃ�
�قȂ�i���|�P�j�̒n�_�̂ǂꂩ�ɓ������m���ňړ�����B�i�P�j���̐��������i�P���������|�P�j
�̒n�_��K�₵�I�����Ƃ��C���̈�b�ł܂��K��Ă��Ȃ��n�_�Ɉړ�����m�������߂�B
�i�Q�j���̐��������̒n�_��K�₵�I�����Ƃ��C�܂��K��Ă��Ȃ��n�_�Ɉړ�����܂ł̕b
���̊��Ғl�����߂�B�i�R�j���̐��������ׂĂ̒n�_��K�₵�I����b���̊��Ғl�����߂�B
�������C�ŏ��ɂǂ����ɂ�����b�Ԃ��b���ɐ�����Ƃ���B
>>421
(1) p_k = (n-k)/(n-1)
(2)
j�b��ɏ��߂Ė��K�n�_�Ɉړ�����m���� q_j = (1-p_k)^(j-1)�Ep_k
�@���K�n�_����k�ł��鎞�Ԃ� t_k �Ƃ���ƁA
�@�d[t_k] = ��[j=1�C��] j q_j = 1/p_k = (n-1)/(n-k).
(3)
�@�d[t] = ��[k=1�Cn-1] �d[t_k] = ��[k=1�Cn-1] (n-1)/(n-k),
���ȁH >>421
1) �K��ς�k���K��n-k
���m���ł��邩��(n-k)/(n-1)
2) m�b��܂ł����ƖK��ς�((k-1)/(n-1))^m
m�b��ɏ��߂Ė��K��((k-1)/(n-1))^(m-1)(n-k)/(n-1)=(n-k)(k-1)^(m-1)/(n-1)^m
��m(n-k)(k-1)^(m-1)/(n-1)^m=(n-k)d/d(k-1)(��(k-1)^m/(n-1)^m)=(n-k)d/d(k-1)(1/(1-(k-1)/(n-1)))=(n-k)d/d(k-1)((n-1)/((n-1)-(k-1)))=(n-k)(n-1)/((n-1)-(k-1))^2=(n-k)(n-1)/(n-k)^2=(n-1)/(n-k)
3) ��(n-1)/(n-k)=(n-1)(1+1/2+�c+1/(n-1)) >>422
>��[j=1�C��] j q_j = 1/p_k
�ȁ[�� S=�o(x.y)€�q^2|x^2+y^2=1}
�̂Ƃ�s^2�͂ǂ̂悤�ȗ��́H�ɂȂ�܂����H
�q=�����ł�
��͂�u���v�ɏ�����̂͂Ȃ��̂ł��傤���H
>>425
�@2�̒P�ʉ~��S�̒��ϏW�� S�~S�i�ɓK���ȍ\�������āj�g�[���X�A�~�ʁA�֊ʁA�h�[�i�c�A�G�������O �ȂǂƉ]���炵���B ���̂�����€�Ƃ͕s�ւȎ�����Ă��
�u���������v�������ϊ����邱�ƂŐ��w�L�����ǂ�ǂ�o�Ă��邱�Ƃ������Ă�����ĂȂ��̂��ȁH
���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��B
������Ɏ����������B
�k�l�_���`���҂�P��NP�\�z���ؖ������l�͂ǂ����̕��������̂ł��傤���H
�����1�l�͓`���ł��A�`�����郌�x���ɒB����l���吨���邱�Ƃ�����k�l�_�����
�o����l�����Ȃ���Ή�������҂��Ȃ���Ȃ��Ȃ�P��NP�\�z�̏ؖ��̂ق������
�����������Ƃ���Ȃ��āA�k�l�_���Ƃ����Z���g���邱�Ǝ��̂ƁA
P��NP�\�z�Ƃ��������������铪�]�͂ǂ����̕����������Ƃ������Ƃł��B
�Ȍ��ɏ����܂�
�ȉ���2���������ɖ������l�ʑ̂����݂��邩�A�܂����̍\�����@�A�����������������Ȃ��ł��傤���B
1.�ǂ̖ʂ̖ʐς�������
2.�ǂ�2�̖ʂ������łȂ�
>>437
�E�K���ȎO�p�`��p�ӂ��܂�
�E�O�p�`�̊e�ӂɂ��āA�ӂ̗��[�Ƃ͈قȂ钸�_��ʂ�A�ӂƕ��s�Ȑ��������A�����ӂ𒆐S���Ƃ��ē���������]�̂ł���~�������܂�
�E�e�ӂō�����R�̉~�����P�_�Ō����A���̓_���S�̒��_�Ƃ��邱�ƂŁA���ׂĂ̖ʂ̖ʐς��������l�ʑ̂��\���ł��܂�
�E���̂S�ʑ̂̊e�ʂ����ł���Ƃ��������������߂ɁA���̎O�p�`���ǂ̂悤�ȏ��������Ȃ���Ȃ�Ȃ����i���邢�͂��̂悤�ȏ������Ȃ��Ƃ����邩�j�ׂ܂� f�����(a,b)�Œ�`���ꂽ���Ƃ��ĉ���2�̏��������l�ł��邱�Ƃ������ĉ�����
lim[x��b-0]f(x)=��
(a,b)���̔C�ӂ̓_��{x_n}��b�Ɏ�������Ȃ�A����{f(x_n)}�̓��Ɏ�������
�����p�`���R���p�X�ƒ�K���g���č�}�o���Ȃ���������Ɨ����o���܂����B
����ŁA�����p�`�𐮐��̖ڐ��肾���ō�}���邱�Ƃ͉\�ł��傤���H
�傫���͑傫���Ȃ��Ă��\���܂���B
�o�����炻�̍��W�̏o�����������Ē����܂����H
2�ȏ�̎��R��n�ɂ����āA
p^n=nq+1
�����f���̑g(p,q)�͑��݂��Ȃ����Ƃ������B
>>440
�����̖ڐ���ō�}�ł���Ȃ�R���p�X�ƒ�K�ō�}�ł����łȂ����H ���̖��ɂ��ĉ������������Ă��������܂��H
�����������Y��ł��܂�

>>443
���ȉ������܂��� �����f���������܂��� ���̖��̌v�Z�����܂�ɖʓ|�Ȃ̂ł����A�ꍇ�����ƌv�Z�ʂ������ł����炷���@�͂���܂��H
a,b�����R���Ƃ��A3����
f(x)=x^3+(a-b)x^2+bx
���l����B
(1)f(x)�̑����ׂ�B���������ʂ͒��ׂȂ��ėǂ��B
(2)���̎���c�ɑ��āA�ȉ��̒�ϕ������߂�B
��[0��c] f(x) dx
>>442
�����Ɛ����ŋ��ꂽ�ڐ���̍��W��m�肽���̂�
�o���Ȃ��Ȃ炻�̏ؖ����m�肽���B
�O��Ɣ�邩�ȁH����͍��W�����邩�������I�ɂȂ����Ǝv������ ���ʂ��������A�ڐ���������o���Ȃ��B
�����ɃX���`��������Ȃ�����
1. ���_��66%�͓��_��60%���x��
2. 150�_���_��99�_��150�_���_��90�_���x��
>>447
> �����p�`���R���p�X�ƒ�K���g���č�}�o���Ȃ�
> �����p�`�𐮐��̖ڐ��肾���ō�}����
����炪�������邱�Ƃł���Ƃ������Ƃ������ł��Ȃ����Ă��ƁH ����������}�͉\�Ȃ�łȂ����H
�핢��Ԃ̒�`�Ŕ핢�ʑ��ɘA���������肵�Ȃ����Ƃ�����̂ł����H
�\�z�`���ʂ̗\�z�a�����肷��Ɛ������Əؖ�����Ē藝�`�ɂȂ�Ƃ��A
�������\�z�a���Ԉ���Ă���Ƃ킩������\�z�`���Ԉ���Ă���\���͍����̂ł��傤���H
>>450
�����ŏo���邩�ǂ��������炳1�������g����R���p�X�ƒ�K�Ȃ��薳�����H�ł���������������v�Z���ʼn����������������H �_�╧�⍂����́A���w�z���Ă���̂ł��傤���H
�����A�_���̃z�U�C�Ă���L�`�K�C�́A�R�e��t���邩���Ă��炢�����B
>>447
�L������15���ł悯���
(623489801858734,781831482468030)
(-222520933956314,974927912181824)
(-900968867902419,433883739117558)
(-900968867902419,-433883739117558)
(-222520933956315,-974927912181824)
(623489801858733,-781831482468030)
(1000000000000000,0)
�ߎ��ł����Ȃ����Ƃɒ��ӂ� >>455
�u �\�zB �� �\�zA �v���^�ł��邱�Ƃ��ؖ��ł��Ă��āA
�Ȃ����\�zB���Ԉ���Ă��邱�Ƃ��ؖ��ł����ꍇ�A�ˑR�Ƃ���
�u �\�zB �� �\�zA �v
�͐^�̂܂܂ł���B�Ȃ��Ȃ�A����͉��肪�U�̖���ƂȂ�A�������Ő^�����炾�B
���R�Ȃ���A�\�zA�̐^�U�ɂ��Ă͉��������Ȃ��B�\�zA���Ԉ���Ă���\����
�����Ƃ��Ⴂ�Ƃ������Ȃ��B �u�s�m�_�v��Wikipedia�Œ��ׂĂ݂�ƁA
���̂��Ƃ̖{���͐l�ɂ͔F�����邱�Ƃ��s�\�ł���A�Ƃ��闧��̂��ƁB
�Ə�����Ă���̂ł����A�u���̂��Ƃ̖{���͐l�ɂ͔F�����邱�Ƃ��s�\�ł���v�Ƃ������Ƃ��������Ă���킯������A�������Ă�悤�ȋC������̂ł����A
����͂����̌��t�V�тȂ̂ł��傤���H
����Ƃ��A�{���ɖ������Ă���̂ł��傤���H
���`�㐔�̓��������Ă��������B
���w�̏Z�l���l����u�ŋ��ϑz�L�����v�������Ă��������B
�㋞�@���G���Ă����H
�ӂ�������@�_���ł���B
�㋞�@�肵���Ă����H
�{����@�����������ƃz���g��߂Ă��������B
�@���邢�́A�X�F���ɂ܂��g�^�ʖڂȁh���Ƃ�̍Œ��ł��c�c�B
�ӂ�������@���b����̖��O���������炶��Ȃ��ł����H
�㋞�@�f���P�[�g�Șb�Ȃ�B����͒��ڊW�Ȃ��Ǝv�����ǁc�c�B
����{�@�͂��B
�㋞�@�����ς��G���Ă����H
�@�������������ɂ��āA�㋞����������ƁA
�u��������Ȃ��Ƃ������Ă���B�ӂ������������Ȃ��ƌ����Ă����I�v
�u�ӂ�����Ȃ�v
�@�ƑS�ے�B4��12�������́u�T���V���v�ł́A�㋞�����̐U�镑���̏ڍׂ��f�ڂ���B
���O�p�`�ȊO�ŁA
3�̕ӂ̒������L�����A
���A3�̊p�����x��Ōv���\�ȎO�p�`�͂���܂����H
�v�́A�S�Ă̕ӂ̒����Ɗp�x���A��K�ƕ��x��ő����O�p�`������̂��A�Ƃ������Ƃł��B
�Ȃ��̂Ȃ�A�ؖ��ł��܂����B
>>470
����܂���Bcos x���L�����Ȃ�Q(exp ix)��Q��2�����ȉ��ł���
[Q(exp 2��i/N):Q]=��(N)�Ń�(N)��2�ƂȂ�̂�N=1,2,3,4,6�݂̂Ȃ̂łR�ӂ��L�����̎O�p�`�̊p��,����2��/�����̌`�̊p�ƂȂ肤��̂�60��,90��,120����������܂���B >>461
�����A�T���N�X
�V���V�e�B�œ��H���ɍ�������܂����₷��� �R�s�y�~�X���Ă܂����A���ꂪ�������ł�
��낵�����肢���܂�
���̖��̌v�Z�����܂�ɖʓ|�Ȃ̂ł����A�ꍇ�����ƌv�Z�ʂ������ł����炷���@�͂���܂��H
a,b�����R���Ƃ��A3����
f(x)=|x^3+(a-b)x^2+bx|
���l����B
(1)f(x)�̑����ׂ�B���������ʂ͒��ׂȂ��ėǂ��B
(2)���̎���c�ɑ��āA�ȉ��̒�ϕ������߂�B
��[0��c] f(x) dx
f(x)����3��������Ȃ������
�R�s�y���ǂ��H
>>473
��Βl�L�������Ԃ����Ă�̂�3�������Ă������H
�����ׂ邾���Ȃ̂ɉ��ʂׂȂ��Ă悢�Ƃ킴�킴�������H
���W�����Ă��炦�킩�邪�ӂ��͂��������������͂��Ȃ�
����đ��ɂ������ʂ��ԈႦ�Ă����Ȃ����ƕs���ɂȂ�
���̖�肪����Ȃ�摜�ŏグ�� �ȉ��̕s�����ŕ\�����̈��}�����A���̖ʐς����߂�B
y^2≤(1+x){1+(1/x)}≤y^2+1
>>477
�������A�o���������ȂƎv�킹�Ď��͊ȒP�ɂ͉����Ȃ��A����Ȗ�肪�����ȁA������́B
���Ƃ��A����Ȃ́B
3�ȏ�̎��R�� n�@���^����ꂽ�Ƃ��A
���R���@���@�́A�ǂ̂悤�Ȏ��R�� x�Az�@�ɑ����A�������@x^n+y=z^n�@�̉��Ƃ͂Ȃ肦�Ȃ��A�Ƃ����B
y�@�͂ǂ̂悤�Ȏ��R�����H �@ >>479
���̂��߂ɂ���Ă���܂��̂ŁA�����I�łȂ����͉����܂��� >>477����ʐϗL���ɂȂ�Hx>0�ɂ�����
sqrt(x+1/x+1) �� y �� sqrt(x+1/x+2)
������
sqrt(x+1/x+2) - sqrt(x+1/x+1)
=1/(sqrt(x+1/x+2) + sqrt(x+1/x+2))
����x������O(1/(2sqrt(x)))�����甭�U����ˁH >>479
�y�A�m�Z�p���܂ޔC�ӂ̖������Ȍ����n�ɑ��A���郂�f��M,N����ј_�����ӂ����݂��āAM|=�ӂ���N|���ӂƂł��邱�Ƃ������A�Ƃ�����肪�킩��܂��� �l��������Ȃ��A�S�����ˁA�W���[
>>480
�s�����Ȗ��������Ȃ����̈�Ȃ̂ł��傤�ˁB >>463
�I�}�G������Ă�̂����t�V�� �_���̖����̂ƁA���_��a��ł��鏑�����݂��������A���b�`���C�ł�����������ǂ����ˁH
>>466
�h���Y�K��������v���h�ɒS���o����Ă܂����B
�u���E�v���l���̒��S�A�Ԃ����z�̖ю�� ���I�v �ю�Ȃ͗��h����A���̒����͕����Ƃ�B���{�͌���Ȃ������Ă�B
���݂܂��̃X���ł����̂��킩��܂��A
������98%�ɂ�����ɂ͍ŒZ��
�Q�[���v���C��
����
�������ɂȂ�Ə���98%�ɂ�����܂����H
�������������I
�ʐ^�\��Ă܂���ł����B�B

�c��v���C�����A�S�ď������Ƃ���
(1933+x)/(1979+x)��0.98
R,R'�F��
I,J�FR�̃C�f�A���AI',J':R'�̃C�f�A��
R/I≅R'/I'�AR/J≅R'/J'�@����I��J���܂ނ�����̑f�C�f�A��
���̂Ƃ�I�f��J'���܂ނ�����̑f�C�f�A���ƌ����邻���Ȃ̂ł���
���ςł�I��I'�AJ��J'���Ή����Ă���̂ł���Ȋ������܂����A�ؖ����킩�炸������₵�Ă��܂�
�킩�����������Ⴂ�܂������낵�����肢���܂�
R,R'�F��
I,J�FR�̃C�f�A���AI',J':R'�̃C�f�A��
R/I≅R'/I'�AR/J≅R'/J'�@����I��J���܂ނ�����̑f�C�f�A��
���̂Ƃ�I�f��J'���܂ނ�����̑f�C�f�A���ƌ����邻���Ȃ̂ł���
���ςł�I��I'�AJ��J'���Ή����Ă���̂ł���Ȋ������܂����A�ؖ����킩�炸������₵�Ă��܂�
�킩�����������Ⴂ�܂������낵�����肢���܂�
>>492
���݂܂���
���ǂ��Ɖ��A�������炢���̂ł��傤���H
�ق�Ƃ��݂܂��� 2300��܂ŕ����Ȃ�����
�L�����悭�Ă悩�����ˁi�悭�Ȃ����j
>>496
���̕s����������������
���������O�H
�A�z�� >>499
���݂܂����ł����ǂ킩��܂���
�{���ɋ����ĉ�����
���݂܂��� �ߋ����X�ؗ�ɃX���[�͍��������w���\���W�Ȃ�
���A2300�Ȃ�
���肪�Ƃ��������܂�
97%�ɂȂ��Ă���98%�ɏオ��܂Ŗ����ꒃ�����ꒃ�����ł��I�I
�T�C�R����6000��U�����Ƃ���Ak�̖ڂ��o���ak�Ƃ���ƁA
a1=976
a2=1160
a3=769
a4=1089
a5=996
a6=1010
�ł������Ƃ����B���̃T�C�R���͕����ȃT�C�R���ł���ƌ����邩�B
�s����(a-b)(b-c)>(c-d)(d-a)�������B
�Ȃ����̂₤�Ȕ������s�����������ꂸ�Ɏc���Ă����̂��B
>>506
�ǂ̕����ɂ��ĉ����̂��ˁH �����̎��삩�ˁH ���`�ʑ�L:R^2��R^2��x��0�ɂ�����sup(|L(x)|/|x|)<1�����Ƃ���
���̂Ƃ��AF:R^2��R^2��F(x)=x+L(x)�ƒ�߂��
det(F)��0�ƂȂ��Ă��邱�Ƃ������ĉ�����
���łQ�����Ɍ���H
�ŗL�l�̐�Βl���P�����Ȃ�
�P�����ĂO�ɂ͂Ȃ��B
y=1/x��1��x��n�̕����̒���Ln�ƁAy=1/x��2��x��n+1�̕����̒���Mn�Ƃ̍��ɂ��āA�Ɍ��l
lim[n����] (Ln-Mn)
�����߂�B
>>493
K��̂Ƃ���
R=R'=K[x]
J=J'=(x^2)
I=(x), I'=(x+1)
�Ŕ��Ⴉ��
R����R'�����Ȃ���Ȃɂ������Ă���悤�ȋC������ >>506
0 < (a-b)(b-c) - (c-d)(d-a) = (b-d)(a-b+c-d),
>>510
���{1+(1/x^2)} dx = ��(1/x)��(1+xx) dx
= ��{cosh(t)^2}/sinh(t) dt�@�@�i���@x=sinh(t)�j
= ��{sinh(t) + 1/sinh(t)} dt
= cosh(t) + log(tanh(t/2))
= ��(1+xx) + (1/2) log{[��(1+xx)-1]/[��(1+xx) +1]},
�����
Ln = ��(1+nn) +(1/2) log{[��(1+nn)-1]/[��(1+nn)+1]} -��2 - (1/2) log{[��2 -1]/[��2 +1]},
Mn = ��{1+(n+1)^2} +(1/2) log{[��(1+(n+1)^2)-1]/[��(1+(n+1)^2)+1]} -��5 - (1/2) log{[��5 -1]/[��5 +1]},
1��x��2 �̕����̒�����
(��5 - ��2) + (1/2) log{[��5 -1]/[��5 +1]} - (1/2) log{[��2 -1]/[��2+1]}
= 1.22201617708663
n��x��n+1 �̕����͕��R�ɂȂ�A�����͂P�ɋ߂Â��B
Ln - Mn �� 0.22201617708663�@�@(n����) �_�͐��w�z���Ă���̂ł��傤���H
���ꂪ�^�Ȃ�_�̓��[�}���\�z�ɑ��ĂȂ�炩�̏ؖ��A���邢�͔���̍��Ղ��c���Ă��锤�B
���݂��Ȃ����͒��z���N�\���Ȃ�
�_�����w�z���Ă��邩����ă��[�}���\�z�ɑ��ĉ��炩�̏ؖ��┽��̍��Ղ��c���Ă���Ƃ͌���Ȃ��̂ł́H
���f���ʂ̖��ŒP�ʉ~������_P�Ƃ����ݒ肪�悭�o�Ă��܂����A
���f���ʂƉ~�͑������ǂ��̂ł��傤��
���f���ʂ̐����𗝉�����̂Ɏ����葁�����炶��Ȃ��H
>>516
���ꂪ�^�Ȃ炠�Ȃ��̐_�͂��̒��x�̐_�Ƃ������ƂɂȂ锤�B >>519
���̒��x���Ă����̂��l�Ԃ̎ړx�ōl�������ʂł����Ȃ��B
�_�̎��_���猩��A�����ʂ̈Ӗ������邩������Ȃ��B >>510
f(x) = 1/x,
f '(x) = -1/xx,
��[1�C2] ��{1+(1/x^4)} dx = 1.132090393306
��[n�Cn+1] ��{1+(1/x^4)} dx �� 1�@�@(n����)
�ӁX�����B
Ln - Mn �� 0.132090393306�@�@(n����) ����������Ԃ��Ăǂ�Ȋ����̋�ԂȂ�ł��傤���H
���sup�Ɖ���inf��
�u�����ɑ����́v�A�u�L���̗�O�������v�Ƃ������t��p���Đ�������
����ɂ��ċ����Ă�������
���@n��2�ȏ�̐����Ƃ���Ƃ��C��(n!)�������ƂȂ邱�Ƃ͂��邩�H
�Ƃ������͂ǂ�����ĉ��������������Ă��������D
>>525
��(n!) = m �Ƃ���
n! = m^2
n �ȉ��̍ő�̑f���� p �Ƃ���
�㎮�̑f�����Ƃ��č��ӂ� p ��1��������
�E�ӂ͕������Ȃ̂Ŋe�f���������������Ƃɔ����� >>526
n��2p�܂ł����āAp�`2p�܂ł͑S�č������ɂȂ�悤�ȏꍇ�͂Ȃ��̂ł��傤���H �}�L�V���E�R���c�F�r�b�`�͓V�˂̒��̓V�˂ł����H
���̖�肨�������Ȃ��ł����H
https://imgur.com/a/aYA2i90
�h���}�ƃR�}�[�V�����̉��������R�}�[�V����
�̉��h���}���P�Ȃ��ꍇ�͎������藧��
�Ȃ����A�i���R�������Ȃ��j
�Ō�ɂS���̃h���}������ꍇ�͐��藧���ǁA
���̂悤�Ȕԑg�Ƃ����̂͂ӂ�����܂����ˁH �܂��A���҂������̍�������̐ݒ���q�ώ��ł��ĂȂ��T�^�I�ȃp�^�[��������
�C�ɂ���ȁB�Ⴆ��20���̃h���}��3����CM���h���}����n�߂Č��݂ɌJ��Ԃ���
211���ɂȂ����狭���I���݂����ȏ�z�肵�Ă�̂�������A���̐ݒ��
�\���ł��ĂȂ���ˁB
�r�f�I�e�[�v�̂���������̉��̖�肾�H
>>531
���肪�Ƃ��������܂��B
�s���̗̍p�����̉ߋ���ł��B B+BS = 112-5[]
S = 4[]+4
T+ST = 82-5[]
BT = 3[]
BST = 2[]+2
0<=[]<=16
�v�Z�ԈႢ���Ă܂����B
�Q�W�l�ł��ˁB�ł����͂T�Ԃ̂R�S�l�炵���ł��B
�{���̎�����肪�Ȃ�����m���Ȃ��Ƃ͌����Ȃ��̂ł����B
>>508
�����番����l���܂��H >>508
���Adet(F)=0�Ɖ��肵�܂�
F�͋t�s��������܂���AFx=y�Ƃ����A�����������l�������Ay�ɑΉ�����x�͕������݂���Ƃ������Ƃł�
���̘A���������̉��̂���2�������Ă��āAa,b(a��b)�Ƃ��܂�
�����
F(a)=a+L(a)=F(b)=b+L(b)
�ƂȂ�܂�
L�����`�ʑ��ł��邱�Ƃɒ��ӂ����
L(a-b)=b-a
���̂Ƃ��A|L(a-b)|/|b-a|=1�ł����A����͉���ɔ����܂� >>509 �����̂������e�ɏ����Ă邶���B >>509
�ǂ��������Ƃł����H
����҂���Ȃ����ǒm�肽���ł� n�����R���Ƃ���B
�Ɍ�
lim[n����] |n^n-(n-1)^(n+1)|
�����߂�B
a,b,c �͐�����a��0�łȂ��Ƃ��A
(1/5)a^2 + (1/3)b^2 + c^2 + (1/2)ab + bc + (2/3)ca
�̍ŏ��l�͂ǂ̂悤�ɋ��߂�����ł��傤���B
>>543
�^��=n^n(1-(1-1/n)^n(n-1))�����E(1-��/e�E��)=-�� >>545
�c�O�A������Ȃ���肾������ ���O�̂�
������Ȃ������
�\��X������ˁ[��
������
>>533
34�l�ō����Ă�B
114+84-(x+3y)+2x+y=200���Ax=2y+2
x+3y��84�ɑ�����Đ��������5y��82�@�� y��16
y=16�̂Ƃ�x=34
>>547
�����Ă݂�
�������ɐk����
n�͏\���傫���Ƃ���B
�ǂ̂悤�ȓ�n�p�`�ł��A�Ȃ��p�Ƃ���<90��-�ÂƂȂ�悤��2�{�̑Ίp�������邱�Ƃ������B�Â͏\�������������Ƃ���B >>530
���ɏ�����Ă��邱�Ƃ��悭���͂��čœK�ȓ�����I�ԃv���Z�X�́A���܂Ńe�X�g�ʼn��x������Ă���͂�����
�s���ӂȂ�������������̂������Ă��Ȃ� >>549
n�p�`�̓��p�̘a�� (n-2)�� ������A�ł����������p �� (n-2)��/n.
���̒��_����o�� (n-3) �{�̑Ίp���́A2�ӂ̓����ɂ���B
�Ȃ��p�Ƃ��ŏ��̂��̂́A(n-2)��/{n(n-4)} �ȉ��B
�Ίp���̑����� n(n-3)/2 �{
���ꂪ 0�`�ɕ��z���邩��A�Ȃ��p�Ƃ��ŏ��̂��̂� 2��/{n(n-3)} �ȉ��B
�A���A���ۂɂ͌����Ȃ��ꍇ�A���s���ɂȂ�ꍇ�������Ƃ���B �\���傫���Ƃ��\���������Ƃ��A������^�����Ė�����������肾�낤��
���Ƃ��Đ������Ăˁ[��B
�͂Ƃ��Ƃ��g���Ď����ׂ������������ƋL�q���Ă݂₪��B
����ňӖ��s�����ɋC�Â��Ȃ��Ȃ������߂�B
>>544
�����������ē���������Ă���ȉ��ɂȂ�_�����߂�B >>552
��ώ��炢�����܂����A��������������
��������F�l�̒m�\����ɖ𗧂Ă܂� >>530
�^�悳�����f���ⓚ���Ƃ��čl����ׂ��Ȃ̂��R�}�[�V������
�ŏ��ɓ���Ȃ����f���̃h���}�̘^�掞�Ԃł��邱�Ƃ͖�蕶�̋�C�œǂݎ���B
���ɁA�������ݒ肳��Ă���ł��낤5��108����Ƃ���B
��蕶�Ɏ���8�̉���
1�F(�h���}�ƃR�}�|�V���������킹���S�̂̕��f���Ԃ��낤��)���f���Ԃ�211���ł���A
2�F20���Ԃ̃h���}�̕��f����3���ԃR�}�[�V����(�ȉ��ACM�Ɨ��L)�������A
3�F�W�����[�h(���ʂ̕��@)��120���^��o����r�f�I�e�[�v�����ׂĎg���A
4�FCM�͘^�悵�Ȃ��A
5�F�ŏ��ɕ��ʂ̕��@(�W�����[�h)�Ńr�f�I�e�[�v�����ׂĎg���A
6�F5�̂悤�Ƀr�f�I�e�[�v�����ׂĎg���A�^��̓r������A3�{�����[�h�̋@�\�ɐ�ւ���A
7�F�h���}�̏I���Ɠ����Ƀr�f�I�e�[�v���I������悤�ɘ^�悷��
(���ʂ̃r�f�I�ɂ̓h���}�I���Ɠ����Ƀr�f�I�̘^�����I������@�\�͂��邾�낤���A�����̈Ӗ����������w)�A
8�F�h���}�����f�����O��CM�͗���Ȃ��A
�͊m���ɂ��ׂĖ��L����Ă���B
����3�A5����A�^�掞�̍ŏ��̑���́A�h���}��120���Ԙ^�悵�ăr�f�I�e�[�v���g���邱�ƂɂȂ�B
����2�A8����A�^��̊J�n����20����ɍŏ���CM��3���ԗ���A
����1�A3�A5�A6�A7�����悤�Ƀr�f�I�e�[�v���g����܂łɂ͍��v4��3���Ԃ�CM�������B
����āA����4����A�͂��߂ɘ^�悵���r�f�I�e�[�v���g��������ɂ́A�^�悳��Ă��Ȃ���12���Ԃ������邱�ƂɂȂ�B
�̂ɁA�^��J�n����120�����O�Ƀr�f�I�e�[�v���g���邱�Ƃ͂��蓾�Ȃ����ƂɂȂ�B
����́A���ʂ̕��@��120���Ԙ^�悵�ăr�f�I�e�|�v���g���������Ƃɔ�����������B
������A�����̌���5��108����ł͂Ȃ����ƂɂȂ�B
�ݒ肳��Ă��铚���̌��ł��낤5��108���オ�ے肳��A�^��̍ŏ��̑��삪�A
�h���}��120���Ԙ^�悵�ăr�f�I�e�[�v���g���邱�Ƃł���ȏ�A�����̌��Ƃ��ċ������Ă���
108�����O�̎��Ԃ́A1��92����A2��96����A3��100����A4��104���� �������I�ɔے肳���B >>530
>>555�̉���7�́u�r�f�I�̘^���v�łȂ��A�u�r�f�I�̘^��v
(�^�掞�ɂ͓����ɘ^��������邩��A�債�ĕς���)�B >>554
�X���`������o��Ȃ�ʂ̃X���ł���Ă��� >>530
�v�Z�����������A���������B
�^�悳�����f���ⓚ���Ƃ��čl����ׂ��Ȃ̂��R�}�[�V������
�ŏ��ɓ���Ȃ����f���̃h���}�̘^�掞�Ԃł��邱�Ƃ͖�蕶�̋�C�œǂݎ���B
��C�œǂނƁA�{���̓����̌��ɂ�105���オ�����Ă��Ȃ��Ƃ����Ȃ��Ǝv����B
���ɁA�����ɂȂ邩���m��Ȃ��u4��104����v���u5��108����v�Ƃ���B��蕶�Ɏ���8�̉���
1�F(�h���}�ƃR�}�|�V���������킹���S�̂̕��f���Ԃ��낤��)���f���Ԃ�211���ł���A
2�F20���Ԃ̃h���}�̕��f����3���ԃR�}�[�V����(�ȉ��ACM�Ɨ��L)�������A
3�F�W�����[�h(���ʂ̕��@)��120���^��o����r�f�I�e�[�v�����ׂĎg���A
4�FCM�͘^�悵�Ȃ��A
5�F�ŏ��ɕ��ʂ̕��@(�W�����[�h)�Ńr�f�I�e�[�v�����ׂĎg���A
6�F5�̂悤�Ƀr�f�I�e�[�v�����ׂĎg���A�^��̓r������A3�{�����[�h�̋@�\�ɐ�ւ���A
7�F�h���}�̏I���Ɠ����Ƀr�f�I�e�[�v���I������悤�ɘ^�悷��
(���ʂ̃r�f�I�ɂ̓h���}�I���Ɠ����Ƀr�f�I�̘^����I������@�\�͂��邾�낤���A�����̈Ӗ����������w)�A
8�F�h���}�����f�����O��CM�͗���Ȃ��A
�͊m���ɂ��ׂĖ��L����Ă���B
����3�A5����A�^�掞�̍ŏ��̑���́A�h���}��120���Ԙ^�悵�ăr�f�I�e�[�v���g���邱�ƂɂȂ�B
����2�A8����A�^��̊J�n����20����ɍŏ���CM��3���ԗ���A
����1�A3�A5�A6�A7�����ׂĖ������悤�Ƀr�f�I�e�[�v���g����܂łɂ͍��v5��3���Ԃ�CM�������(23�~5��115��120)�B
����āA����4����A�͂��߂ɘ^�悵���r�f�I�e�[�v���g��������ɂ́A�^�悳��Ă��Ȃ���15���Ԃ������邱�ƂɂȂ�B
�����ɁA�r�f�I�e�[�v�ɘ^�悳���h���}�̕��f���Ԃ͘^��J�n����105����ɂȂ�B �����ϕ��w�Ƃ����{��
�ua>1�̂Ƃ��Aa^(1/n)��1 (n��+��)�������v
�Ƃ������̉������
a^(1/1) > a^(1/2) > a^(1/3) > ...
�������Ƃ��Ĉ����Ă����̂ł����A
����͉��̐��藧�̂ł����H
�ؖ��̑��
n�Ɋւ��ĒP������ ���� ���ɗL�E �� 1�Ɏ���
�Ƃ������̂ł�
>>530
(>>558�̑���)
�^�悳���Ă���108����̂Ƃ��́A�^�撆�̏�ԂɂȂ�B120���^�悳���ăr�f�I�e�[�v���g����Ƃ����A���f�h���}�̘^�撆�B
�^�悳���Ă���104����̂Ƃ����A�^�撆�̏�ԂɂȂ�B120���^�悳���ăr�f�I�e�[�v���g����ƁA���f�h���}�̘^�撆�B
������A�ݒ肳��Ă��铚���̌��ɂȂ邩���m��Ȃ��u4��104����v�A�u5��108����v�͗����ے肳���B
��C��ǂ�Ōv�Z���ē������o���ƁA�{���̓����̌���105����ƂȂ邾�낤����A
104����A108�����O�̎��Ԃ́A1��92����A2��96����A3��100���� �������I�ɔے肳���B
�A���A�{���̓����̌��ɋ������Ă��Ȃ���Ȃ�Ȃ����낤�u105����v���A�_���I�ɂ�>>555-556�Ƃقړ��l�ɂ��Ĕے肳���B >>548
��34�l
���肪�Ƃ��������܂��B
��蕶��ǂ݊Ԉ���Ă��܂����B >>559
a>1��a^(1/n)>1��a^(m/n)>1��a^(p/q+m/n)>a^(p/q) >>562
�܂肱���������Ƃł���
a��1����n��1�ɂ��āA
a^(1/n)/a^(1/(n+1))��a^((1/n)-(1/(n+1)))��a^(1/(n(n+1)))��1
�܂�a^(1/(n+1))��1��0
�����a^(1/n)��a^(1/(n+1)) n���\���傫�����A�ǂ̂悤�ȓ�n�p�`�ɂ��Ă�����2�{�̑Ίp�������݂��A���̐����p�Ƃ�89��<��<91���ƂȂ�悤�ɂł��邱�Ƃ����߂��B
>>562 >>563
����ID�ς���Ă��܂�������҂ł��B
�w���̔�r������̂ɂ͎v������܂���ł����B���肪�Ƃ��������܂��I ���̐���A������3����f(x)�͑��݂��邩�B
A
���قȂ�2�̐���m,n�ɑ��āA
��[m��n] f(x) dx = ��[i=m,...,n] f(i)
>>566
�R�e�t����������Ă��� ���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��B
���z�ʉ݂��ĉ��H
���ƁA���z�ʉ݂Ő��璛�~���炢�҂����Ƃ��ĉ\�H
>>566
f���萔���łȂ��Ƃ���ƁA�C�ӂ�n�ɂ��āAn����n+2��3�ȏ�̋ɒl�������ƂɂȂ薵������B
����đ��݂��Ȃ�
������������Ȃ���H �J�I�X��腖��剤�͂ǂ����̕��������ł����H
>>566
�C�ӂ̑��قȂ�2�̐���m,n�ɂ���
���Ă��ƁH
m<k<n�̂Ƃ�
��[i=m,...,n]f(i) = ��[m��n]f(x)dx
= ��[m��k]f(x)dx + ��[k��n]f(x)dx
= ��[i=m,...,k]f(i) + ��[i=k,...,n]f(i)
������ f(k) = 0�B
�C�ӂ̐���k�ɑ��āAm<k<n�ƂȂ鐮��m,n��
��Ɍ����邩��Af�͒萔��0�B
�R�����ł͂Ȃ��ˁB
�C�ӂ̑��قȂ�2�̐���m,n���Ă��ƁH
��[m��n] f(x) dx = ��[i=m,...,n] f(i) n���\���傫�����A�ǂ̂悤�ȓ�n�p�`�ɂ��Ă��A����2�{�̑Ίp���ł��̐����p�Ƃ�89��<��<91���ƂȂ���̂����݂���B
���̂��Ƃ������B
�~����ɂ��_���߂��Ɏ��ƑΊp���̕����͂قړ����B
>>566
f(x) = 4ax^3 +3bx^2 +2cx +d,�@(a��0)
�Ƃ�����
��[m�Cn] f(x) dx = [ ax^4 +bx^3 +cx^2 +dx ](x=m�Cn) = a(n^4-m^4) +b(n^3-m^3) +c(n^2-m^2) +d(n-m),
��[i=m�Cn] f(i) = a{nn(n+1)^2 -mm(m-1)^2} +b{n(n+1/2)(n+1)-(m-1)(m-1/2)m} +c{n(n+1)-(m-1)m}+d(n+1-m),
�ӁX������
a{nn(2n+1)+mm(2m-1)} +b{n(3n+1)/2 +m(3m-1)/2} +c(n+m) +d,
���ꂪ0�ɂȂ�悤�� a�`d �����߂�B �Ƃ̍ő�l�͖]�ނ����O�ɋ߂��ł���A�ƁB
>>575
�ł͏�����lj����Ă������� >>574
�A�z����
�ϑz�����ŏo�肵���C�ɂȂ��Ă��Ȃ��H ���̖���iP�j���^�ƂȂ邽�߂̏����ɂ��ďq�ׂ����́iS�j�̋߂�B
�iP�jn���\���傫�����A�����iA�j�����ǂ̂悤�ȓ�n�p�`�ɂ��Ă��A����2�{�̑Ίp���ł��̐����p�Ƃ�89��<��<91���ƂȂ���̂����݂���B
�iS�j��n�p�`�̂���3���_A,B,C�ɂ��āA�i�@�j<��ABC<�i�@�j�ł���B
>>544
a���Œ肷��B
b�ŕΔ������ā@(1/2)a + (2/3)b +c = 0,
c�ŕΔ������ā@(2/3)a + b + 2c = 0,
����� (b�Cc) = (-a�Ca/6) �ōŏ��l aa/180
�@a/6�������ɂȂ�ꍇ������̂ŁA���ۂ́��ȏ�B
(a�Cb�Cc) = (�}1�C��1�C0) �̂Ƃ��ŏ��l 1/30 lim[n����](1/n)*{(n+1)(n+2)�c�2n}^(1/n)=4/e
�̏ؖ���������܂���B
>>583
(����) = {(1+1/n)(1+2/n)�c(1+n/n)}^(1/n) = {��[k=1�Cn] (1+k/n)}^(1/n),
log(����) = (1/n)��[k=1�Cn] log(1+1/k)
�� ��[1�C2] log(x) dx = [ x�log(x) -x ](x=1�C2) = 2 log(2) -1,�@(n����) >>576 �̗�
b=d=0 �̂Ƃ� f(x) �͊���ŁA
��[-n�Cn] f(x)dx = 0,
��[i=-n�Cn] f(i) = 0,
����Af(x) = f(0) (�萔�����j�̂Ƃ���
��[m�Cn] f(x)dx = (n-m) f(0),
��[i=m�Cn] f(i) = (n-m+1)f(0),
�ƂȂ�B >>584
���肪�Ƃ��������܂��B
��_n>0,��_n���Ȃ��[k=1 n]��_k�����B����������+���ł����Ă��悢�B�Ƃ����藝��p���Ă̏ꍇ�����肢�o���܂����H >>582
�Ō�̍s�̌��_��
����ȑO�̍l�@����ǂ������A���ł݂��ׂ���̂ł��傤�� ���݂܂���A�ȒP�Ȗ��Ȃ̂ł���
����d�����`��1�l�ł���ƂP�Q��������A�a��1�l�ł���ƂP�T��������B���̎d�����`���R���Ԃ�����A�`�Ƃa�̂Q�l�ʼn����Ԃ����ďI������B�`���n�߂Ă��牽���ڂŎd�����I�������B
�����͂W���ڂȂ̂ł����A�r�������킩��܂��肢���܂�
Let the amount of the task be 60.
A does 60/12 = 5 a day,
and B does 60/15 = 4 a day.
A worked 3 days, i.e. did 5 x 3 = 15,
and 60 - 15 = 45 is remained.
It will be fulfilled in 45/(5+4) = 9 days.
>>470
���Z�~�̃o�b�N�i���o�[���߂Ă��瓯���悤�Ȗ�肪������ >>587
(b�Cc) ���S�������킽��ŏ��l�� aa/180 �ȏ�ł��邪�A�����Ɍ������ȏ�ɂȂ�B
|a|��3 �̏ꍇ�� 1/20 �ȏ�ƂȂ�A1/30 ���傫������A�ŏ��ł͂Ȃ��B
a=�}2 �̏ꍇ�� 1/45 �ȏ�ƂȂ邪�A�����Ɍ���� (b�Cc) = (-a�C0) �̂Ƃ� 2/15, �ŏ��ł͂Ȃ��B
a=�}1 �̏ꍇ�� 1/180 �ȏ�ƂȂ邪�A�����Ɍ���� (b�Cc) = (-a�C0) �̂Ƃ� 1/30 �ƂȂ�i�ŏ��l�j�B
--------------------------------------------------
(�Q�l)
a���Œ肵�āA(b�Cc)�ʓ��Łi-a�Ca/6) �̎���Ƀ�/2�����F
�@b = Bcos(��/2) + Csin(��/2) -a,
�@c = -Bsin(��/2) + Ccos(��/2) +a/6,
�@�A���Atan�� = 3/2, sin�� = 3/��13�Ccos�� = 2/��13
�@�@�@�@tan(��/2) = (��13 -2)/3,
���̂Ƃ�
�@(�^��) = (1/5)aa + (1/3)bb +cc +(1/2)ab +bc +(2/3)ca
�@= aa/180 + {(4-��13)/6}BB + {(4+��13)/6}CC
�@�� aa/180, >>564 >>574 >>581
���������D���ł��ˁB
���͎���ƕ��s/�����s�Ɍ������Ƃ����肵�܂����A�H�ɐ����Ɍ������Ƃ����肷����̂�����炵���B
�́X�̂��Ƃł����A�ア�������̃��J�j�Y���Ƃ��āA�ɒB�搶�i���j�����͎�����
�����������Ɣ������������Ƃ������ɋ�������icanted spin�Ccanted ferro.�j���f�����l�����炵���B
���݂̓W�����V���X�L�[�E��J�iD-M�j���ݍ�p�ɓ��ꂳ�ꂽ�悤�ł����c (A+B)�E(B+C)�E(C+~A)
����H�Ńu�[���㐔���o�Ă�����
��̘_�����Z�����̘_�����Z�ɂǂ��ϊ������炢���H
(A+B)�E(C+~A)
>>593
�I���I�t�\����Ĕ�r���邾�� >>593
(A+B)�E(C+~A)=B�E(C+~A)+C�E(A+B)
(�敪�z���AB�EC=B�EC+B�EC) >>595
�A���^�̐S������Ԃ킩��� �r�炵�̐S�����낤�Ƃ��邠�͂������ɂ�
�P�̒c��G���ړIP���s���Ƃ�
�c��G�ɏW�������L1�AL2�AL3�c�Ƃ����
L1�AL2�AL3�c���������邱�ƔۂƂ������C���c��G�ɑ��Ă����
L1�AL2�AL3�c�͂ǂ��ɏW�����ĖړIP���s���ׂ���
�������A�c�̂�V���ɂ��邱�Ƃ͔F�߂��A�����ŖړIP��B�����邱�Ƃ͂ł��Ȃ����̂Ƃ���
R^n�̓_���lim[n����](a_n)=b�̂Ƃ�B={a_n | n��N}��{b}�Ƃ����B�����U��ԂɂȂ�Ȃ����Ƃ͂���̂ł��傤���H
���A���U�ɂȂ�Ȃ��Ƃ����Ban=0��{an}�� {0}�Ƃ����U�W���ł͂Ȃ��B
a_m=sin(m+1)��-sinm���Ƃ����B
|a_m-(1/10)|���ŏ��ɂ���m�����߂�B
x^3+xy - xz^2+yz
��������������t���łՂ�[��
�l�ɂ͂킩��܂���B���₷�݂Ȃ����B
>>607
���̂悤�ȏꍇ�A��Ԏ����̏����������ɂ��Đ�������̂���ł�
x�̎�����3�Ay�̎�����1�Az�̎�����2�ł�����Ay�ɂ��Đ������܂��傤
x^3+xy - xz^2+yz
=y(x+z)+x^3-xz^2
=y(x+z)+x(x-z)(x+z)
=(x+z)(y+x(x-z))
=(x+z)(x^2-xz+y) x^3-3x+1
���������v���[�Y
>>609
�ȒP�Ȗ��ɂ͂������X������ł��� 10101(2)��11(2)
����111�ō����Ă܂����H
>>609
(x+z)(y+x(x-z)) �ɂ͂Ȃ��Ă���ł����ȂJ�b�R3�Ɏ��߂Ȃ��Ƃ����Ȃ��悤�ȋC�ɂȂ��Ă܂����B
���肪�Ƃ��������܂� �l�ʑ�ABCD��AB���܂ނ��镽�ʃ���2�̗���S��V�Ƃɐؒf����B
��CD�̒��_��M�Ƃ���B���̂Ƃ��AS��V�������ł��邽�߂̕K�v�\�������́A
�u����3�_A,B,M��ʂ�v
�ł��邱�Ƃ������B
��ABC�ɂ����āAAB=6 CA=8 cosA=1/4�̂Ƃ��A
���_B�����CA�Ɉ����������ƕ�CA�Ƃ̌�_��D�A
���_C�����AB�Ɉ����������ƕ�AB�Ƃ̌�_��E�Ƃ���ƁA����ED�̒����͉��ɂȂ邩�H
�Ƃ�����肪�킩��܂���A
���������A���_B�����CA�ɐ�������������BA�Ɗ�����Ǝv���̂ł����A�v���Ⴂ�ł��傤���H
>>616
�����܂���A���Ⴂ���Ă܂����A���͂��܂���͂�킩��܂���ł��� >>613
���Έʑ������U�ȕ����ʑ���Ԃ̂���ł���
���̏ꍇ�A
{1/n | n��1�ȏ�}�͗��U���
{1/n | n��1�ȏ�}��{0}�͗��U��ԂłȂ�
�ł��傤���H ���̒�`�Ȃ�
>>601
�͕��ʂ͗��U�ɂȂ�Ȃ�
���U�ɂȂ�͓̂r�����炸����b�̂Ƃ� >>622
�ʑ���Ԃ����U�ł���Ƃ́A�C�ӂ̕����W�����J�W���ƂȂ邱�Ƃł�
�ʑ����X�̕����W��A�������ʑ���ԂɂȂ�Ƃ́AA�̊J�W���n���AX�̊J�W����A�̋��ʕ����ŗ^�����邱�Ƃł�
>>619�̏�̏W��S�́A���̈Ӗ��ɂ����ė��U�ƂȂ�܂�
�Ȃ��Ȃ�A1/n�͏����ɂ����ė��U�I�Ȃ̂ŁA���̓_���Ǘ�������悤�ȃ��[�N���b�h�ʑ��ɂ�����J�W����I�Ԃ��Ƃ��ł��A�����S�Ƃ̌����A���Ȃ킿1/n�͕����ʑ���Ԃɂ�����J�W���ƂȂ�A���Ȃ킿S���̔C�ӂ̓_�͊J�W���ƂȂ邩��ł�
�����̉҂��āA����Ȃ��Ƃ��킩��Ȃ���ł��� >>623
���̒�`�Ȃ�>>619��
S={1/n | n��1�ȏ�}��{0}
�͑��Έʑ��ɂ�����{0}�͊J�W���ɂȂ���K�X�B
0���܂ނǂ�ȊJ�W��O���Ƃ��Ă�O��S={0}�ɂȂ��̂ł�H ����S�͏�̏W�����ƌ������͂��ł����ǁH
>>622���萔�����Ȃ��Ɨ��U�ɂȂ�Ȃ��Ƃ��ق����Ă��̂ŁA���U���킩��Ȃ��낤�ȁA�Ǝv���������ł� >>623
>>>619�̏�̏W��S�́A���̈Ӗ��ɂ����ė��U�ƂȂ�܂�
�W�Ȃ����Ƃ��������Ȃ��˔\�̎����傩 >>628
���Ȃ����҂ɉR�������Ă���̂Ƀ_���o�����Ă����ł���
�p���������Ȃ���ł����� >>626
�ӂ�K�v�͖���������ł�
�ӂ邱�Ƃ͖W�����Ă��Ȃ� >>632
>>622�ʼnR�̃��X�𐂂ꗬ�������Ƃ͎ӂ�Ȃ��Ă��ǂ��̂ł��傤���H >>633
>>619
��{1/n | n��1�ȏ�}�͗��U���
�ƂȂ��Ă܂���
b�������Ă�킯�ł͂Ȃ��̂� �Ă�����
�r�����炸����b����Ȃ���
{an|n��N}��{b}�����U�ɂȂ������肢
������
�W�Ȃ����Ƃ��������Ȃ��˔\�̎����傩
>>638
���E�Q������@���킩��܂���
��낵�����肢���܂� >>634
�g���`���J���Ȃ��Ƃ������Ď���҂�f�킵�����Ƃ͎ӂ�Ȃ��̂ł��� >>641
���Ȃ����E�����@�������Ă�������
�킩��Ȃ���ł����H >>623
>�����̉҂��āA����Ȃ��Ƃ��킩��Ȃ���ł���
�W���W������ >>644
�������E�����@���킩��Ȃ��Ȃ�āA�����̉҂̃��x�����ĒႢ��ł��� >>630
>�p���������Ȃ���ł����� >>646
�������E�����@���킩��Ȃ��Ȃ�Ēp���������Ȃ���ł����H >>636
���U�ʑ������Η��U�ɂȂ��Ă܂��� >>651
�����������E������@�͂킩������ł����H
����������������
����Ƃ��A�����̉҂��Ď��E���ł��Ȃ����炢���x�����Ⴂ��ł����H
�p���������ł��� >>652
�s���Ȃ瑁�����E���������ǂ��̂ł͂Ȃ��ł����H >>654
�N
�����Ɍ����Ă����������悳���� >>655
���e�Ƃ�����ł���
�����̔��F�߂����Ȃ����߂ɑ���̂����ɂ���炵���ł�
���킢�����ł��� >>650
>���U�ʑ������Η��U�ɂȂ��Ă܂���
w
�g���`���J���Ȃ��Ƃ�������Ȃ��͎̂���҂Ɏӂ�Ȃ��Ă�����ł���
>>619
>���Έʑ������U�ȕ����ʑ���Ԃ̂���ł���
w
>>620
>�����ł��� �����̂��Ƃ���������̂��Ƃ̂悤�ɂ��邱�Ƃ����ł��Ȃ���ł���
�a�C�Ȃ悤�ł�
���������ɕa�@�ɍs�������������ł���
����������x�ꂾ�Ǝv���܂����ǁA�����͗ǂ��Ȃ邩������܂����
>>650
>���U�ʑ������Η��U�ɂȂ��Ă܂���
�W���W������ �a�l�͂����ɂ͂����܂����
�������@����������
�[��ɉ����Ă�N������
�����͌��j����
>>664
>�a�@���Ȃ�����
�W���W������ ���_�a���҂��͂悤�������܂�
�����͕a�@�s���܂��傤��
�^�P�P�P�P�P�P�P/�_
�P�P�����P�P�P�P�_/|
�Q (�Le`)�@>>615 / |
�P|(����)~�Q�Q_�^| |
�n| �a�P�P�P�P�a | /
�Q| �a ���@�� �a |/
_�@`�a�Q�Q�Q�Q�a�^���_C�A���_D���畽�ʃ��ɐ���CE�A����DF�������B
���p�͓������B��_�Ԃ̒��_M�͓�_�����B�䂦��CE��DF���Ȃ킿��ABM���ʂƂ���O�p��C-ABM�ƎO�p��D-ABM�͓����̐ςł���B ���j�͂܂��o�J�̂Ȃ��肪�c���Ă��
r�͎����An�͐��̐����Ƃ���B
f(x)=(1-rx)(1+x+x^2+...+x^(n-1))
�͂����̋ɑ�l����ыɏ��l����邩�B
�p����25��������������
�u�В������߂��x�݁B�v�ƕ������Ă��܂����B
�ςȃ��b�e������͂�߂ĉ������ˁB
�N�������Ă��邩������Ȃ��悤�ɂ��Ȃ��Ɣ����ł��Ȃ�
�ڋ��Ȋ�̌����Ȃ����{�l��
�u�����܂���B�v
�ƊO���畷�����Ă��܂����B
���́A�N�������ӂ����̂������ł��܂��A����ł����̂ł��傤���H
�{���Ɏ���ȑΉ����Ǝv���܂��B
�O���Ăǂ��ł���
�N���ǂ�ȏŌ������̂������ł��܂��A����ł����̂ł��傤���H�@
�X���̓��e�ɂ�����Ȃ��{���Ɏ���ȃ��X���Ǝv���܂��B
�ȏ�A�X���`�ȃ��X���炢�����܂��B
>>674
�u���b�N�������Ƃ��ł��Ȃ��Ȃ�
����15��
�ǂƂ���10��
��25���Ǝv������ �ڋ��҂̂��������J���邱�Ƃ́A���v�Ɏ�����ƍl���܂����B
>>674
�Ƃ�����2002�N�̃X���b�h���Ă������� ����@���ƃA���N�T���h���E�O���^���f�B�[�N�͂ǂ����̕��������́H
>>674
25��1�[�B�[��23���Ă���Ȃ��ƂȂ�Ƃ��c >>674
>�v�Z�~�i�[�E�s�`�b
�A�z�Ȃ� �Q�T���Ə��w���̕W�����x���̖��ł��ˁB
���̖��̃��x���ƍ����傫���̂��C������B
���ԂȂ��ςݏd�˂�
�Ƃ��Ȃ����23�ł��ł��邩�������
>>616��������Ȃ����H
(��14)/2�@�O>>670
�^�P�P�P�P�P�P�P/�_
[�P�P���� �����P�_/|
[�Q�i(-_-)-_-))�@/ |
�P|`(��u~)U��U��^| |
�n| �a�҃�~UU~�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/�@
�Q| �a ���@�� �a /�@
�P�_�a�Q�Q�Q�Q�a/�@ /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@��,�c�~�|
�Q�Q�Q�Q�Q�Q�Q��`,`;,
�Q�Q�Q�Q�Q�Q�Q_U��U�;
/�Q/�Q/�Q/�Q/�Q;~U U~
/�Q/�Q/�Q/�Q��_/�Q/�Q
/�Q/�Q/�Q/�Q/�Q/�Q/�Q
AD��ABcosA��6�~(1/4)
��3/2
CD��8�|(3/2)��13/2
���l��AE��2�ABE��4
BC~2��BE~2�{EC~2
��4~2�{60
��56
BC��2��14
��ED��(1/4)BC��(��14)/2 >>616�������ȁB�O>>688
�^�P�P�P�P�P�P�P/�_
[�P�P���� �����P�_/|
[�Q�i(`o`)-_-))�@/ |
�P|`(��u~)U��U��^| |
�n| �a�҃�~UU~�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/�@
�Q| �a ���@�� �a /�@
�P�_�a�Q�Q�Q�Q�a/�@ /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@��,�c�~�|
�Q�Q�Q�Q�Q�Q�Q��`,`;,
�Q�Q�Q�Q�Q�Q�Q_U��U�;
/�Q/�Q/�Q/�Q/�Q;~U U~
/�Q/�Q/�Q/�Q��_/�Q/�Q
/�Q/�Q/�Q/�Q/�Q/�Q/�Q
AD��ABcosA��6�~(1/4)
��3/2
CD��8�|(3/2)��13/2
���l��AE��2�ABE��4
BC~2��BE~2�{EC~2
��4~2�{60
��76
BC��2��19
��ED��(1/4)BC��(��19)/2 �쒆���痂���̓쒆���}����܂ł��āA�n����360���ȏ㎩�]���Ă��ˁH
������̓쒆����365��ڂ̓쒆���}����i���̂Ƃ����]�O���œ����ʒu�ɖ߂�Ƃ���j�܂łɒn����366�]���Ă���͂�����
>>690���z�ƌ��͈Ⴄ�łˡ�S(�L�E�ցE�M)�O>>689���͒n���ɑ��Ă��������ʂ������Ă�B���ǒn���͑��z�ɑ��Ă��������ʂ������Ă͂��Ȃ��B
�n�������z�̂܂����������̂�365��������N�ɁA�n����365�]���Ă邵�A366��������N�ɂ́A366�]����B�n���͑��z�̂܂��������]���邠�����Ɉ�]�v�Ɏ��]�����肵�Ȃ��B���Ƃ͈Ⴄ�̂���A���Ƃ́B
�^�P�P�P�P�P�P�P/�_
[�P�P���� �����P�_/|
[�Q�i(-_-)-_-))�@/ |
�P|`(����)U��U��^| |
�n| �a�҃�~UU~�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/�@
�Q| �a ���@�� �a /�@
�P�_�a�Q�Q�Q�Q�a/�@ /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q >>691
�N�������Ȃ��Ă����� �P�P�P�P�P�P�P�P/�_
�P�P�P�����P�P�P�_/|
�Q_�@(-_-))�@�@�@/ |
�P|�_(��u~)�Q�Q�^| |
�n| �a�҃ҁP�P�a |/|
�Q| �a ���@�� �a | |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/�@/
�Q| �a ���@�� �a /�@/|
�P�_�a�Q�Q�Q�Q�a/�@/ |
�Q�Q�Q�Q�Q�Q�Q�Q_�^| |
�P�P�P�P�P�P�P�P�a | |
���@���@���@���@�a |/
�Q�Q�Q�Q�Q�Q�Q�Q�a�^_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/��]�v�Ɏ��]���Ă�̂��������Ȃ��B
��ABC�̐��S��H�Ƃ��A����AH��BC�̌�_��D�A����BH��AC�̌�_��E�A����CH��AB�̌�_��F�Ƃ���B
3�̔�AH:HD�ABH:HE�ACH:HF�A�̂��������2:1�ƂȂ�Ƃ��A��ABC�͂ǂ̂悤�ȎO�p�`���B
2:1���Ă��Ƃ�H����ABC�̏d�S�B
CH:HD��2:1
��CHD��60��
����ABC�͐��O�p�`
���������u�n���̏o�v�Ƃ������f�����悭�o��邪�A
����͉q�����ړ����Ă邩��n��������Ă���悤�Ɍ�����킯��
���ʏ�̒�_����͒n���͂��������ꏊ�ɂ���
x,y�ɂ��Ă̘A��������
ax+(1-b)y=0
bx+(1-a)y=0
��-1≤x≤1����-1≤y≤1�͈̔͂ɉ������悤��a,b�̏��������߂�B
p�𐮐��Ƃ���Ƃ��An^2+p���f���ƂȂ�悤�Ȑ���n�����݂��邱�Ƃ������B
�����͔R����S�~�̓��ł͂���܂���
�l�p�`
�c��300cm�@����200cm�@�c�̒��S���Wx �����@�@���̒��S���Wy�@����
���A�^����ꂽ���́@�l�p�`�̊p�̍��W(����A�����A�E��A�E��)�̋��ߕ�
�v�Z���������ĉ������B
�\�L��4�̒l�ł��B(x,y)���W�ł͗L��܂���B
�����C�����܂��B
�����XY���ɗL��l�p�`
���̒��́A�����Ȏl�p�`�ŗL��B�e�A�p���W�̋��ߕ��ł����B
��ӂ̒���3�̐��O�p�`T�̏d�S�𒆐S�Ƃ���~C�́AT�̊e�ӂ�3�����_��ʂ�BT�̊O������C�̓����ł���̈�̖ʐς��A�����_�ȉ��ꌅ�܂ŋ��߂�i�����_�ȉ��ڈȉ��͐�̂Ă�j�B
>>712
�~C�̖ʐρ���
�~C���̐��Z�p�`�̖ʐ�
��{(��3)/4}�~6
��(3��3)/2
���l��(�~C�̖ʐρ|�~C���̐��Z�p�`�̖ʐ�)��3
����/3�|(��3)/2 �������������B�O>>713
�~C�̖ʐρ���
�~C���̐��Z�p�`�̖ʐ�
��{(��3)/4}�~6
��(3��3)/2
���l��(�~C�̖ʐρ|�~C���̐��Z�p�`�̖ʐ�)��2
����/2�|(3��3)/4
��1.57�c�c�|1.299�c�c
��0.27�c�c
�����_�ȉ����ʂ��̂Ă�ƁA
(����)0.2 ����n��ɏZ�ސl�X�̒ʘb���ԂɊւ��āA�ȉ��̂��Ƃ��������Ă���B
�E���傤��0�b�̒ʘb���N���邱�ƁA�����4���Ԉȏ�̒ʘb���N���邱�Ƃ̊m���͂��ꂼ��0�ł���B
�Ex�͎����Ƃ���B0<x<14400�ɂ����āA���傤��x�b�̒ʘb���N����m��p(x)��0�łȂ��B
�E�����Âɑ��A���傤��x+�Õb�̒ʘb���N����m����{1+1/(100+��^2)}p(x)�ł���B
���̂Ƃ��A����ׂɑI�ʘb��1���Ԉȏ�2���Ԉȉ��ŏI���m�������߂�B
>>715
����ȕ��z���肦�ւ���B
F(x)�z���Ƃ��Ċex�ɑ�p(x)=F(x+0)-F(x-0)>0�Ȃ�r(x) �� (F(x-0),F(x+0)) �� Q��I�ׂ邯�ǁA���̂Ƃ�r�͔���Z�����W��������Z�����W���ւ̒P�˂�^���Ă��܂��B ���i���j�� x^n + ax^(n-1) + bx^(n-2) + cx^(n-2) + �E�E�E + d�Ƃ���n�����������ɂ���
��_[0,1] { f(x) }^2 dx ���l����Ƃ��A���ꂪ�ŏ��ɂȂ�̂�
�@�@a=(2n-1)/(2n) ���� b=c=�E�E�E=d=0 �̂Ƃ�
�Ƃ�����ł��傤���B
grapes�Ƃ����`��\�t�g�ŐF�X�����Ă��炱�̂悤�ȗ\�z���������̂ł����A�ǂ��ł��傤���B
>>717
���߂łƂ��A���W�����h���������̍Ĕ��� >>717
f(x)�����W�����h��������Pk(x)��
f(x) = ��[k=0,n]ck*Pk(2x-1)
�̂悤�ɓW�J���� L^2�m�������Ƃ�� Pk�̒��𐫂��
��[0,1]{f(x)}^2dx = ��[k=0,n](ck)^2*��[0,1]{Pk(2x-1)}^2dx
�Ƃ���킳���B���������� c0=c1=�c=cn-1=0 �̂Ƃ����ŏ��ŁA���̂Ƃ�
f(x) = Pn(2x-1)/C[2n,n] = (1/C[2n,n])��[k=0,n]C[n,k]C[n+k,k](-1)^(n-k)x^k
�ƂȂ��āA�ŏ��l��
��[0,1]{Pn(2x-1)/C[2n,n]}^2dx = 1/{(2n+1)C[2n,n]^2}
���Ȃ݂�L^���m�������ŏ��ɂ���̂̓`�F�r�V�F�t������ >>717
grapes�������
�����I�ɑ���ł��邵
function view�������悤�Ȋ�������� >>721
GRAPES �� FUNCTION VIEW �� GeoGebra �Ɣ�ׂ�ƕ�����Ȃ�
���Y�����牞���������̂��� ���{�l�̂���t���[�\�t�g�����܂������W���Ȃ��̂͂���ς�l�ł���Ă邩�炶��Ȃ����Ȃ��B
�������̂ق��̓R�~���j�e�B�[�����Ă݂�ȂŔ��W�����Ă����B
���̓_�����������{�l�͉p��ł��Ȃ�����Ȃ��B
�������ꂩ��̎���t���[�E�F�A�̗ނ�Git Hub�Ƃ��ɂ����Ă��Ȃ��ƃ_���Ȋ�K�X�B
0≤��≤2�Ƃ���B
x=4sin��(1-cos��)
y=4cos��(sin��+cos��)
�ŕ\�����Ȑ��ň͂܂�镔���̖ʐς����߂�B
>>719 >>721
��ʂɌ�����̂ł��ˁB
�邶���h���������̓E�B�L�Ō��܂��������܂�ȒP�����ł��Ȃ��̂�
721�̏������݂ƍ��킹�ėǂ������������Ǝv���܂��B
���肪�Ƃ��������܂��B ���Ȍ������Ȃ��������ꔭ�����nj������Ă�Ɠr�[�ɓ���Ȃ邩��Ȃ�
�w���@�ʼn����炵����ł����ǁA������O�̂��Ƃ������ƌ����ĈӊO�Ɠ���肪�o�܂���
���:�Ђƌ��̒��ŁA�ǂ̗j�������Ȃ��Ƃ�4��邱�Ƃ������B
����
����j����3��ȉ��̂Ƃ����͍ő�ł�4��
���̂Ƃ��ő�ł�3+4*6=27�������Ȃ�
>>729
���������Ă�������Ȃ��́H�\���͂��邯�� >>730
���ق�
28���őS���̗j��4��o��킗
���Ƃ͂���ɒlj��ɂȂ邾�� �`���I�ɂ��Ȃ炱��
>>730
�R��ȉ���������Ȃ��j��������Ɖ��肷��B
���̗j���̍ł���������X���Ƃ��A���̌��̍Ō�̓���M���Ƃ���B
X���̂V���O�͓����łȂ��̂ŁAX-7��1�ł���B�܂��A���̗j���͂R��ȏ㌻��邱�Ƃ��Ȃ��̂ŁA�O�T�Ԍ�A�܂�21����͓����łȂ��B�܂�M��X+21�ł���B
X-7��1���X��8�ł���AX�͐����Ȃ̂�X��7�ł���B���l��M��X+20�Ȃ̂ŁAM��X+20��7+20=27�ƂȂ�B
�����̓��t��27���ȉ��ƂȂ錎�͂Ȃ��̂ŁA�R��ȉ���������Ȃ��j��������Ƃ����ŏ��̉��肪���ł��邱�Ƃ��킩��B >>734
�������Ȃ����
�ʐ�=|��[0,2��]xy'd��|
�ł����܂�������>>725�̖���0<��<��<�̃�,����P(��) = P(��)�ƂȂ�_��������
�ʐ�=|��[0,��]xy'd��|+|��[��,��]xy'd��|+|��[��,��]xy'd��|+|��[��,2��]xy'd��|
�Ő�Βl�̒��̕����������_�̑O��ŕω����邩��킯�Ȃ��ƃ_���B
�ł��̃�,����explicit�ɂ͏o�Ȃ��̂Ōv�Z�ʔ��[�Ȃ��B
�o���Ȃ��͂Ȃ����낤���ǖʔ������Ȃ�Ƃ��Ȃ��̂ł��C�������Ȃ��B >>737
���m�ɂ�P(0) = P(��)�AP(��)=P(��)�łQ�Ȍ������Ă܂��B���C���N����B ����j����3��ȉ���������Ȃ��Ƃ���
����ƈꌎ�͏��Ȃ��Ƃ�28������̂�
���Ȃ��Ƃ�25���ȏ�͎c���6��ނ̗j���݂̂������
6��ނ�25���Ȃ̂ŁA�ǂꂩ��̗j����5���
�����x�ƒu��
�����ŘA��������T�Ԃ̊ԂɑS�Ă̗j��������邱�Ƃɒ��ӂ����
���߂�x�Ɠ��ڂ�x�̊ԂɎc���6��ނ̗j�����S�Č����
���l�ɁA���ڂƎO��ڂ̊ԁA�O��ڂƎl��ڂ̊ԁA�l��ڂƌ܉�ڂ̊�
�ɂ�x�ȊO�̗j���������
�]����x�ȊO�̗j���͂��ꂼ��4��ȏ�o�ė��鎖�ɂȂ�
����͏��߂�3��ȉ������o�Ă��Ȃ��j��������Ƃ������Ƃɖ�������
����Ė����������ꂽ�̂ŏ��߂̉ߒ��͌��ł���A�S�Ă̗j���͎l��ȏ㌻���
>>725
�O���[���̒藝���
��(1/2)(xdy - ydx) = ��[0�C2��] (1/2){x(dy/d��) - y(dx/d��)} d�� = 8��,
>>726 >>729
���Ȍ����Ȃ� >>740 �͑�ԈႢ�B��艺���܂��Borz
>>737 >>738
�� = 0.96455795189993440168
�� = 2.9624328650873071464 >>745
�������Ă���0〜2�Őϕ��������̂�
|���ɉ�镔���̖ʐς̑S�́[���ɉ�镔���̖ʐς̑S��|
�ɂ����Ȃ�Ȃ�����킯�Ȃ��Ƃ�����B ���S�Ɍ��藝�̏ؖ����ă��[�����g������d�v�݂����Ȃ̂ł����A���[�����g������Ă��̌`�ȊO���肦�Ȃ��̂ł��傤���H
���܂��܃��[�����g����̒�`�ɂ������̂ł����S�Ɍ��藝�I�ɕ֗��Ȃ̂����̌`�Ȃ����ŁA�{���͕ʂ̌`������蓾���肵�Ȃ���ł��傤���H
���������Ȃ̂Ŏ����ōl���Ă݂����̂Ńq���g�Ȃǂ��������܂�����K���ł��B
�����܂����ł�����낵�����肢���܂��B
>744
����ˁB>>725�͎��Ȍ������Ă���Ƃ���ɓ���Ȃ�Ƃ����b�m��Ȃ��œK���ɍ���Ă邾���������B�o���Ƃ͂Ȃ����낤���ǖʔ����Ƃ��Ȃ�Ƃ��Ȃ��B >>746
���̓��̓~�X���ĂˁH
���������ł����Ȍ����͂��邪 >>737 >>738 >>741
P(0) = P(��) = (0�C4)
P(��) = P(��) = (��2�C6-2��2)
sin�� = {1+��(��2 -1)} /2 = 0.821797126452791
sin�� = {1-��(��2 -1)} /2 = 0.178202873547209
cos�� = {(1-��2) +��(1+��2)} /2 = 0.5697802058284711
cos�� = {(1-��2) -��(1+��2)} /2 = -0.983993768201566
cos(2��) = sin(2��) = 1 -1/��2 -��(��2 -1) = -0.35070103409213
sin(2��) = cos(2��) = 1 -1/��2 +��(��2 -1) = 0.936487474717190
�� + �� = (5/4)�� >>741 >>752
���ł�
�� + �� = (5/4)��,
sin�� + sin�� = 1,
cos�� + cos�� = 1 - ��2, >>748
�����Ă邱�Ƃ��B���Ȃ̂ő��l�ɂ͗����ł��Ȃ��B��l�Ŋ撣�� t���S�������Ƃ��A�Ȑ�
x=t
y=(t+1)|sint|
xy���ʂɂ�}������B
�����͎����Œ�`����܂����A���f���Ɋg������Ƃǂ�Ȑ��E���L�����Ă��܂���
lim[n����] f(n)=l�̂Ƃ�
����������n^(-f(n))��1<l�Ȃ�����A1>l�Ȃ甭�U���邱�Ƃ������ĉ�����
>>757
������Œ�`�����ƌ��������H
V��C�x�N�g����ԂȂ�
dim_CV=2dim_RV ��Ζ����Ɩ��n���I�͂ǂ����̕��������ł����H
>>758
��n^(-l)�����@�i1<l�j�Ȃ̂Ŏ��� >>762
�_�Ɩ��͂ǂ����̕��������ł����H >>755
y=|sinx| (x��-1), y=-|sinx| (x<-1)�̃O���t�������āA�ɒl��y=x+1��ɗ���悤�ɐL�k������ �~K:x^2+y^2=1�ƁAK�ɓ��ڂ��鐳�O�p�`ABC������BA(0,1)�ł���ABC��x���ɕ��s�ł���B
K�̌�BC�̂����_A���܂ޕ������_P������AP�͓_B�Ɠ_C�ɂ͓��B���Ȃ����̂Ƃ���B�ȉ��̖₢�ɓ�����B
�i1�j��PBC�̐��S��H�Ƃ���BH����PBC�̓����ɂ���悤��P(x,y)�ɂ��āAx�͈̔͂����߂�B
�i2�j��PBC��90���Ɍ���Ȃ��߂Â��Ƃ��A��PBC�̐��SH�͂ǂ̓_�ɋ߂Â����B
�i3�jH�̋O�Ղ����߂�B
���SH�̍��W�������ł��܂���B���ʐ}�`���g�������܂����@�͂Ȃ��ł��傤���B�������肢�܂��B
>>759
����[���P�킩���
���ۘ_�I�ɐ�������Ƃǂ��Ȃ́H
�����ł����������������}�`���l���邱�Ƃ��Ă��邩�� >>769
ABCPH��O���n�_�Ƃ���ʒu�x�N�g����abcph�Ƃ���
h=b+c+p
������h��B,C��ʂ蒆�S��x����Ŕ��a1�̉~��K�ȊO�̉~(�̈ꕔ)
�����瓚����K��BC�Ŕ��]�������~��̗��BC�ł��ȁB >>771
����
P�̊�Ղ���ʂȂ�H�̋O�Ղ͗D�ʁAP�̊�Ղ��D�ʂȂ�H�̋O�Ղ͗�ʂł��B >>771>>772
��������ł悩������ABC�͐��O�p�`������P�̋O�Ղ��D�ʂ�H�̋O�Ղ���ʂ�OK. >>769
���ʐ}�`���g���ĂƂ������ƂȂ̂Łc
(1)
���S���O�p�`�̓����ɂ���̂́A�O�p�`���s�p�O�p�`�̂Ƃ��Ȃ̂ŁA
��PBC<90���A��PCB<90�����
-��3/2<x<��3/2
�i��BPC�͏��60���Ȃ̂ŁA�l������K�v�Ȃ��j
(2)
��PBC=90���ƂȂ�Ƃ��A���S��B�ƈ�v����̂ŁA��PBC��90���Ɍ���Ȃ��߂Â��Ƃ�H��B�Ɍ���Ȃ��߂Â��B
(3)
��HBC=��HPC�A��HCB=��HPB���A
��HBC+��HCB=��HPC+��HPB=60��
�� ��BHC=120��
����āAD(0,-1)�Ƃ��āAH�̋O�Ղ�D�𒆐S�Ƃ��锼�a1�̉~���́A����BC���猩��A�Ɠ������ɂ����BC�i�������A���[�������j
(3)�ɂ��Ă����Əڂ��������Ȃ�A���_��O�Ƃ��āA��BOC=��BHC���AH�́�OBC�̊O�ډ~��́ABC���猩��O�Ɠ������ɂ���A�Ƃ������ƁB b�x�N�g����a�x�N�g�������̐��������߂�
|b��|cos��=(a���Eb��)/|a��|
p_n�͕��ꂪn���̐����ł���悤�Ȋ����̂����Aa_n=|��2-(p_n)|���ŏ��ɂ�����̂ł���B
a_n��10�i�@�\�������Ƃ��A�����_���ʈȉ��ɕ���0�̌���b_n�Ƃ����Bb_n��n�̑召���r����B
>>778
n��1�ȏ�̐����Ƃ���B
q_n��10^n�ȉ��̍ő�̑f���Ƃ���ƁA10^n/2 < q_n < 10^n�ł���Aq_n��n���̐����B
r_n�́A���ꂪq_n�̕����̂����Ac_n = |��2 - q_n|���ŏ��ɂ�����̂Ƃ���ƁA
���炩��0 < c_n < 1/(2q_n)�ł���Ar_n��1��2�ł͂Ȃ��̂ŁAr_n�͕��ꂪq_n�̊����B
����āAp_n�̒�`���0 < a_n �� c_n�ƂȂ�A
1/(2q_n) < 1/(10^n)���A0 < a_n < 1/(10^n)
�� b_n �� n
�Ȃ��An=1�̎��ׂ��b_1=1�ƂȂ�̂ŁAb_n > n�Ƃ͌����Ȃ��B
p_1=7/5�Ca_1=0.01421�c 
���R�̖��̃e�X�g�Łu�O�p�`�͉�����܂����H�v�Ƃ������ł��B
�}�Ɋւ��āA���ɒ��߂͂���܂���ł����B
���͂X�Ɠ����ԈႦ�ɂȂ�܂����B
���������ɂ́A
�u�����āA�O�p�`���ĂR�_�ƂR�̐������H
�@�S���q�����ďo�������c�͐��̐^�ɓ_�����邵�A���̓_�Ɍq�����Ă�����͒����i180�x�j�Ƃ͌���Ȃ����H
�@������A�q�����Ă郄�c�͂����ĊO�����̂ɁA�A�A�v�ƁB
�����搶�Ɍ��������ǁA�K���ɂ�������ꂽ�����ł��B
���̌������Ƃ��ނ����Ǝv���̂ŁA�[���̂������������Ă��������̂ł����A���܂�������܂���B
�������������͂���܂��ł��傤���B >>780
�摜���݂�ƁA�ǂ��݂Ă��ӂ��M�U�M�U���ĂĒ����ł͂Ȃ��ł�����A�O�p�`�̌���0�ł��� >>780
�ł����O�p�`�̐^�ɋt���̎O�p�`����������Ƃ̎O�p�`�͎O�p�`����Ȃ��Ȃ���Ă��ƁH�ĕ����Ă�
xsin(1/x)��1��x�̂Ƃ��P�������ł��邱�Ƃ�����
�ϐ����Ђ�����Ԃ���(�t��)���̂�0��x��1�ŒP�������ł��邱�Ƃ�������̂ŁA���̊���1��x�ŒP������
������Ȍ���(�G���K���g��)���͗��ɂȂ��A���ȁH
�l�ʑ�PABC�̕�PA,PB,PC��ɂ��ꂼ��_D,E,F���Ƃ�A��ABC=2��DEF�ł���悤�ɂ���B
���̂Ƃ��A�̐ς̔�i�l�ʑ�ADEF�j/�i�l�ʑ�PABC�j�̍ő�l�����߂�B
>>780
�o��҂̖]�ޓ������߂Ă���琳����������������_�����ċ����Ƃ� �}�b�v���S�{�ɂȂ����Ƃ��ɐ��l�ύX���Y�ꂽ���Ƃɂ�鏉�S�҂���Ƒ����������Ȃ�悤�Ȏ�镺��o�O��������I
>>780
���������������Ă�|�C���g�������������畡�����邩������Ȃ��ł����A
�P�D���̓r���ɓ_�������Ă��A�Q�̐������q�����Ă���̂ł͂Ȃ��A
�@���Ƃ��ƒ��������������Ă��̓r���ɓ_��������ƍl����悢�̂ŁA
�@�ς��ƌ��Œ����ɂȂ�悤�ɏ����Ă���ΐ������Ȃ��Ă������̂����
�@�搶�͏������̂��Ǝv���Ă�������
�Q�D�傫���O�p�`�̊e�ӏ�ɂQ�_��������Ă���������A�^��
�@�R�̐��������ƂP�_�Ō���邩�ǂ����킩��Ȃ��Ƃ������Ƃ�
�@�S�z���Ă��邩������Ȃ����A�e�ӏ�̂Q�_���A�ӂ��O��������悤�ɂƂ�A
�@�K���P�_�Ō���邩��A�}�ɂ͉������܂����͂Ȃ�����
�R�D���̐}���A�X�̏������O�p�`��ӂŌq�������̂��Ɨ��������Ƃ��Ă��A
�@���̂X�̎O�p�`�������`�i���̂����R��180����]�������́j�ł���A
�@�O�p�`�̓��p�̘a��180���ł��邱�Ƃ���A�������q�����Ē���������
�@������Ƃ���͖{���ɒ��������ɂȂ��Ă��āA4�q���������̂�
�@9�q���������̂������ƎO�p�`�ɂȂ邱��
�ȏ��������āi���ɂQ��R�̂��炭���[�������āj
���̎q�������C�ɂ��Ȃ������|�C���g�ɋC�Â������Ƃ���������J�߂Ă����܂��傤�B
���̏�ŁA����͂Q��R�̏𗝉�������Ƃ��낪���̎�|�ł͂Ȃ��A
�������ڂ�����������Ƃ������Ďq����������������̂ŁA�搶�Ƃ��Ă�
�P�̂悤�ɂς��ƌ���M�p���đ傫���O�p�`���܂߂Đ����ė~���������̂��Ƃ���
���X��l�̎���̕��������������܂��傤�B ���͕K�v�\��������n��3k�|1�Ő��藧���Ȃ����Ƃ������Ȃ���Ȃ��̂��
�����Ə�肢�������͂���܂����H



�s�p�O�p�`OAB�ɂ���
OA=a OB=b OC=c �Ƃ�����
���ρ@��(OA)���(OB)��
a,b,c��p���ĕ\��
�Ƃ������œ�����
(a^2+b^2-c^2)/2
�ɂȂ�炵���̂���
���̉��Ɏ���܂ł̉ߒ��������Ăق���
>>792
������������
����ƈӖ���������
3Q ���ɊW�Ȃ��̂ɂ����o��킯�Ȃ��B
OC=c �Ȃ�Ȃ���
AB=c ���낤����
�W�J�̖��ŁAx��-3 y��1/3�Ƃ���
(x-2y)(x-y)-2y^2
���Ȃ̂ł����A���̖�肪�����܂���B
���肢���܂��B
�����āA�W�J�̎��ł̕����̂������悭�킩��܂���B
(x-a)^2��x^2 -2(-a�~-a)x +a^2
�Ȃ̂ł��傤���B����Ƃ��A-2(a�~a)�Ȃ̂ł��傤���H
�������������B
>>799
-2(-a�~-a)x�ł�-2(a�~a)x�ł��Ȃ���
�{((-a)�{(-a))x�܂��́|(a�{a)x�Ȃ̂Ł|2ax�ɂȂ� n * (n-1) * �c * (n-(m-1)) = n! / (n-m)!
���̎��ϊ��̕��@�������Ă�������
>>802
> n * (n-1) * �c * (n-(m-1))
����ƕ��q��m�I�����Ă݂� >>799
�܂��͓W�J�B
(x-2y)(x-y)-2y^2
=x^2-2xy-xy+2y^2-2y^2
=x^2-3xy
x=-3 y��1/3�����B
�^��=(-3)^2-3(-3)(1/3)
�@�@=9+3
�@�@=12 >>805
�{�P����B(n-m)!��� >>790
�����Ƃ����������ĉȂ����B�Ȃɂ���ɂ����Ƃ��������Ȃ��B
�u���[�o�b�N�X�ɂ���Ȃ�v�������{�P���ĉ��̂��Ă��ȁB
�������w�`���̗ǖ�100�\�ǂ����ŗǂ���@���w�� (�u���[�o�b�N�X)
�D�L���A�[�@�ł��Ƃ��邯�ǁB ���茳�ɂȂ�����͂�����͎v���o���Ȃ����ǃO���t�ɑ��čs���Ή������đ���ɑ��ĕs�ςł��鎖�������I��
>>801���� >>804����
���肪�Ƃ��������܂��B
�����̐��w�̋��t�̋��������G�ŁA�悭�킩��Ȃ������̂ł����A��������Ɨ����ł��܂����I
���肪�Ƃ��������܂��B >>809
�������Ⴀ�̓��e�͍Č��ł��Ȃ��̂�... ��5�������Ă�������
ax��xa�͂��ꂼ��v�Z�͂��Ă݂��̂ł�

>>812
�Ⴀ�Ƃ͓����ɂ��邾������� �A���N�T���h���A�̃f�B�I�t�@���g�X�ƃI���Q�l�X�͂ǂ����̕��������ł����H
>>814
�����猩����k�A���v�X�͐�[���H �}�X�^�[�f�[�����̖���\��t����A�z������I�Ɍ��ꂽ��������N���������Ƃ��邯��
>>790�̓������̉������N�����Ă������ق������������� �����������y���ɓ�����ł�
n�̐ԋ���k�̐���������E�ֈ��ɕ��ׁA�����K0�Ƃ���B
���̗�́A�����F�̋����A������2�ȏ����ł��邷�ׂĂ̕����ɑ��āA�����Ɉȉ��̑���iA�j���s���B
�iA�j�e�����̂��ׂĂ̋�����菜���A�����ɐԋ�1�Ɛ�1������������B
���̑����1��s���ē����鋅�̗��K1�Ƃ���B�ȉ����l��K2,K3,...�ƍs���A����iA�j���s���镔�����Ȃ��Ȃ�����I������B
�ԋ��Ɛ���ׂɕ��ׂ�K0�����Ƃ��A�I������܂łɁiA�j���s���̕��ς�n��k�ŕ\�킹�B
>>813
�v�Z���Ԉ���Ă���̂��c�������܂����ׂȂ���ł����

>>814�܂�ɂ��̂Ȃ݂����܂ǂׂɂ݂��Ă��H
�O>>804
�^�P�P�P�P�P�P�P/�_
[�P�P���� �����P�_/|
[�Q�i(-_-)-_-))�@/ |
�P|`(��u~)U��U��^| |
�n| �a�҃�~UU~�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/�@
�Q| �a ���@�� �a /�@
�P�_�a�Q�Q�Q�Q�a/�@ /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@��,�c�~�|
�Q�Q�Q�Q�Q�Q�Q��`,`;,
�Q�Q�Q�Q�Q�Q�Q_U��U�;
/�Q/�Q/�Q/�Q/�Q;~U U~/�Q/�Q/�Q/�Q��_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q >>819
�����o�Ă邶���
a=d,b�C��,c=0 �E���W���ʏ��2�̕�����
C:y=3x^2-2 , D:y=kx^2 ( k>0 ) ���قȂ�2�_�Ō�����Ă���
⑴k�̒l����肤��͈͂� �A< k < �C �ł���B
⑵2�̌�_�̂��� x���W�����ł���_��A�Ƃ���� k=1�̂Ƃ��̓_A�ɂ����������C�̐ڐ�L�̕������� y=�Ex-�G �ł���B
⑶ ������C�Ɛڐ�L�� y���ň͂܂ꂽ�}�`�̖ʐς� S=�I �ł���B
���ς��g���̂ł��傤���H ��낵�����肢���܂��B
>>822
������́A���ς��g���̂ł��傤���Ƃ������Ƃł��ˁB�킩��܂����B
�������������܂��B���ς��g���܂��B ��w�̉ۑ�Łu���f�����Ȃ������炱�̐��ɑ��݂��Ȃ��������͉̂����v���Ă����ۑ�ł����ǂȂ���H
�����ŕ��������������Ǝv��
>>818
������Ƃ��Đ������Ă�H
�Ԑ�
�̏�ԂɂȂ�����
�ԐːԐԐːԐːԐԐˁc�c
�ʼni���ɏI����̂���Ȃ��́H ��\�҂Ɛ��w�҂͂ǂ����̕��������ł����H
>>825 >>826�@�T���N�X
�A�����߂�A���Ⴀ�u���f���̑���ɗ��p�ł��鐔�Ƃ��v�Z�v���Ă���H ���f�����Ȃ�
��C���Ȃ�
���㐔��̑��݂���ʂɌ����Ȃ�
���f�����Ȃ�������A�l�������x�N�g�����Ȃ��������������
�����̑g(x,y)�ɏ�肭���Z�����ĕ��f����C�Ɠ��^�ɂȂ�悤�ɏo����B
R[x]/(x^2�{1) ���l���Ă��悭�āA�����C�Ɠ��^�ɂȂ�B
���f�����Ȃ��Ă��A�����̑̌n���g���Ύ����I�ɂ͕��f�����g���Ă��邱�ƂɂȂ��āA
���̐����玸������͉̂��������B�������A�u���f�����Ȃ�������v�Ƃ�������̈Ӑ}��
�u���f����C�Ɠ��^�ɂȂ�悤�ȑ̌n��(���Ǖ��f���Ȃ̂�)�����֎~�v
�Ƃ����Ӗ��ł���Ƃ��l������B���̏ꍇ�AC�Ɠ��^�ɂȂ�悤�ȑ���Ƃ�
�ǂ̂悤�Ȃ��̂Ȃ̂����E�������܂��Ȃ̂ŁA���⎩�̂ɕs��������B
���Ƃ��A�����Ƌ��������ꂼ������͈̔͂����Ōv�Z���邱�ƂŁA
�u�\�ʓI�ɂ͎����͈̔͂ł����v�Z���ĂȂ����ǁA���̎��Ԃ�C�Ɠ������Ƃ����Ă���v
�Ƃ������|�����\�ł���B�Ƃ����킯�ŁA���{�I�ɂ́A���̎��⎩�̂�������Ȃ��悤�Ɍ�����B
���f�����������ƂŖ��m�Ɏ�������̂ƌ����A
�u���f���Ƀ}�b�`�����Ώۂ͕��f���ŋL�q���Ă����X�b�L������̂ɁA
�@�����������̂f�����g�킸�ɕ\������ƕ��G����ȕ��͂ɂȂ�v
�Ƃ����A�ǐ��Ɋւ�����̂����ł͂Ȃ����B
>>833
�l�����ł����ւ��Ă��܂��Ə�@������ɂȂ�̂ő呹�Q�ł��Ȃ��B
�s����ۂ��C���[�W�ɂȂ�B
�������� i�Cj�Ck �̓p�E���̃X�s���s��ƑΉ�������B >>822
3x^2-2=kx^2 (k>0)�\�\�@
(3-k)x^2-2=0
���ʎ�D=-4(3-k)(-2)>0
3-k>0
k�̒l����肤��͈͂�
0<k<3
2�̌�_�̂��� x���W�����ł���_��A�Ƃ����
k=1�̂Ƃ��@���2x^2=2
x=1(x>0)
�_A(1,1)�ɂ����������y=3x^2-2�̐ڐ�L�̕�������y=3x^2-2���������ƁA
y'=3x
�_A(1,1)��ʂ�A�X��3�̒�����y=3x-2
������C�Ɛڐ�L�� y���ň͂܂ꂽ�}�`�̖ʐς�
S=��0~1{(3x^2-2)-(6x-5)}dx
=��0~1(3x^2-6x+3)dx
=[x^3-3x^2+3x]0~1
=1-3+3
=1
����Ȋ����������H (�O�\�N�قǑO�̐`���[�g�̋L��)�O>>820 >>822�O>>838�C���B
3x^2-2=kx^2 (k>0)�\�\�@
(3-k)x^2-2=0
���ʎ�D=-4(3-k)(-2)>0
3-k>0
k�̒l����肤��͈͂�
0<k<3
2�̌�_�̂��� x���W�����ł���_��A�Ƃ����
k=1�̂Ƃ��@���2x^2=2
x=1(x>0)
�_A(1,1)�ɂ����������y=3x^2-2�̐ڐ�L�̕�������y=3x^2-2���������ƁA
y'=6x
�_A(1,1)��ʂ�A�X��3�̒�����y=6x-5
������C�Ɛڐ�L�� y���ň͂܂ꂽ�}�`�̖ʐς�
S=��0~1{(3x^2-2)-(6x-5)}dx
=��0~1(3x^2-6x+3)dx
=[x^3-3x^2+3x]0~1
=1-3+3
=1 ����Z��/���w���w�ŊȒP�ɃG���K���g�ɉ����܂����H
���������Ȃ狳���Ă�������
�]���藝��2��p���ē����܂������A�I�ɊȒP�ɉ�����̂��Ȃ��Ǝv�����₵�܂���

�����s��Ƃ����̂����邯��
���̒�`�Ɛς����ł��邱�Ƃ������ɂ����Ȃ�
>>829
���ꂱ���s�Z�ł��傤
i�̕ς��ɐ}�̍s����l���������������
�ʎq�͊w�f���̐��E�ő������V�����[�f�B���K�[�����������ʓI�ɂ͓������ƕ�����
�v�Z�̂��₷��������Ă��邩�������
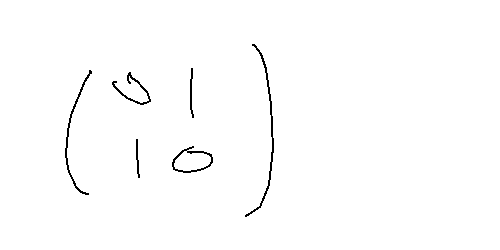
>>840
�o��ʂ�ӂ`�a�̐����ƁA
�q��ʂ�ӂ`�b�̐����Ƃ̌�_���s�Ƃ��A�s���琳���`�̊e���_�֕⏕���������܂��B
�܂��A�o����`�Ɍ������ċ����Ucm�̓_���o'�A�q����`�Ɍ������ċ����Qcm�̓_���q�Ƃ��A�⏕���o'�q'�������܂��B���̕⏕���͒��_�r��ʂ�܂��B
�����̕⏕���ɂ���āA�O�p�`�`�a�b�́A�S�̍����ȎO�p�`�̑g�ƁA�O�p�`�`�o'�q'�ɕ�������܂��B
����ɂ���āA�l�p�`�o'�a�b�q'�̖ʐς������`�̂Q�{�A���O�p�`�`�a�b��136/143�{�A�܂��A�l�p�`�`�o�s�q�̖ʐς�30cm2�Ƃ������Ƃ��킩��܂��B
���̎l�p�`�`�o�s�q�̖ʐς͎O�p�`�`�a�b�Ɛ����`�̖ʐς̍��ɓ������Ȃ�܂��B
����炩�玮�����ĂĖʐς����߂�Ɛ����`�̖ʐς�(136/5)cm2�ƂȂ�܂��B �ł����H
����Ƃ����Ȃ��̕����ȒP�ł��傤���H
�����悭�킩��܂���...
>>840�O>>839
AP���AT:TP��1:6�ƂȂ�T���Ƃ�B
AR���AU:UR��7:2�ƂȂ�U���Ƃ�B
�����`PQRS��(1/2)(��ABC�|��ATU)
��(1/2){(13�11/7)�|1}��ATU (��)88/7 A��TU����()8//7(/117��APR
��(68/7)(1/7)3��7(^2�|3^2
��(68/7993��(0
��3(08849))100 >>840�O>>847�r�����琔���������Ă�B�����B
AP���AT:TP��1:6�ƂȂ�T���Ƃ�B
AR���AU:UR��7:2�ƂȂ�U���Ƃ�B
�����`PQRS��(1/2)(��ABC�|��ATU)
��(1/2){(13�11/7)�|1}��ATU
��(68/7) ��ATU
��(68/7)(1/7)��APR
��(68/7)(1/7)3��(7^2�|3^2)
��(68/49)3��40
��(408/49)��10
�ēx������łI
(408/49)��10 >>846
�����͂ЂƂłȂ��Ă����Ǝv���܂�
������̔��z�́A
�܂��A�O�p�`�`�a�b�̂����A�����`�Ɋ܂܂�Ȃ������̖ʐς����߂悤�Ƃ����Ƃ��납��X�^�[�g���Ă��܂��B
���̎O�p�`�o�a�p�Ƃq�b�p���A���ꂼ��90����]�����Đ����`�̒��ɔ[�߂Ă݂��Ƃ���A���܂��l�p�`(�`�o�s�q)���ł��܂���
���̎l�p�`��Ίp���`�s�ŕ��������璼�p�O�p�`���Q�ł����̂ŁA�ʐς�30cm2�Ƌ��߂��A�����`�̖ʐρ{30cm2���O�p�`�`�a�b�̖ʐςƂ킩��܂����B
���̎����������܂����p�ł��Ȃ����ƍl���ĕ⏕���������Ă���������ł��B >>849
�����̎O�p�`�o�a�p�Ƃq�b�p���A���ꂼ��90����]�����Đ����`�̒��ɔ[�߂Ă݂��Ƃ���A
�����̂Ƃ���A
�O�p�`�o�a�p���A���_�o���Œ肵���܂ܒ��_�p�����_�r�Əd�Ȃ�܂ʼn�]������
���l�ɂq�b�p���A���_�q���Œ肵���܂ܒ��_�p�����_�r�Əd�Ȃ�܂ʼn�]������
��������ƁA���̂Q�̎O�p�`�̕ӂa�p�ƕӂb�p�͂҂�����d�Ȃ�A���l�p�`�`�o�r�q�ƍ��킹�ĂЂƂ̓ʎl�p�`�`�o�s�q�ɂȂ�܂��B >>840�O>>848�����͈�݂�������B�l�����畉���B
AP���AT:TP��1:6�ƂȂ�T���Ƃ�B
AR���AU:UR��7:2�ƂȂ�U���Ƃ�B
�����`PQRS��(1/2)(��ABC�|��ATU)
��(1/2){(13�11/7)�|1}��ATU
��(68/7) ��ATU
��(68/7)(1/7)��APR
��(68/7)(1/7)3��(7^2�|3^2)
��(68/49)3��40
��(408/49)��10
��26.330�c�c
���5cm��
(����)(408/49)��10c�u >>851
����͂����ƁA�Ȃ���APR��3��(7^2�|3^2) �ɂȂ�̂ł��傤�H xy���ʏ�̋Ȑ�
y=k(x-x^3)
x=k(y-y^3)
�����ی��Ń������������L�_(��,��)�����悤�Ȏ���k�̒l�͈̔͂����߂�B
>>841
�P�[���[���i�������j�͔���̂��������@�������藧���ʂ��A�m�����͏�@�I�ł���B�i�m���������́j
�P�U�����ȏ�ɂȂ�ƁA�m��������@�I�ł��Ȃ��B�i����q�����݁j
��R�O�Y�@�u�e�ɂ��Ė삾���ڂł͂Ȃ��|�Γc�X���̐��U�v�@���t���� (1992)�@254p�D551�~ �P�[���[���A�s������������ȁB
�@�ł��A�P�[���[���͍s��\�����ł��Ȃ���
>>855
�s��ŕ\���ł���@�ˁ@�����������藧��
�����������藧���ʁ@�ˁ@�s��ŕ\���ł��� ���̖��(1����)�ɑ��Ď�(2����)�̂悤�ɉ����̂ł����A���͂���őS���ł��傤��
�摜���h���Ă��݂܂���


���̖��(1����)�ɑ��Ď�(2����)�̂悤�ɉ����̂ł����A���͂���őS���ł��傤��
�摜���h���Ă��݂܂���


�i�{�P�ɔ���������Ă��Ƃ��H�j
�̂̓x�N�g����͂͂S�����ł���Ă��炵�����ǁA����CG�Ƃ��Ŏg���Ă�
50�l���ē����a�����̐l������m���ł����A365/1*1/364�F1/363�c�c�Ƃ����������
�v���̂ł����A�����ł͂Ȃ��āAA�����B�������a�����̊m����1/365�AA�����C����
���l��1/365�c�c�ƍl���āAA����Ɠ����a�����̐l������m���� (364/365)^50�B�����50�l
�J�肩�������炻��̂����^50�����߂�m���ł���ƍl����͉̂����Ԉ���Ă���̂ł��傤���H
A����ƈႤ�a�����̊m���� (364/365)^50�B
�ł��ˁA���߂�Ȃ���
>>856
>�����������藧���ʁ@�ˁ@�s��ŕ\���ł���
���Ƃ����łˁH ���^�ɂȂ�Ȃ��Ƃ������Ƃł�����Ȃ�܂����
>>852��APR�̍������O�����̒藝�ŏo���܂��B
�O>>851
��APR�����PR�~(1/2)�~����(A��PR�̋���)
��6�~(1/2)��{AP^2�|(PR/2)^2}
��3��(7^2�|3^2)
��3��(49�|9)
��3��40
��6��10 >>866
PR=6�Ƃ����̂͂ǂ�����o���܂������H
�Ƃ������APR=6���킩���Ă����炻�����琳���`�̖ʐς������o�܂��� >>867R����Ȃ���U�ł����BP�AQ�AR�AS�����ꂼ��TB�ABC�ACU�AUT�̒��_�ƂȂ�悤�Ɏl�p�`TBCU��܂莆�ƌ����ĂĐ����`�̕ӂŐ܂�Ԃ��܂��B�߂����������܂�Ƃ��̊����ł��B��ATR�����[�Ȃ킯�ł��B�O>>866(U��R���߂����ēǂ݂܂�����)
��APU�����PU�~(1/2)�~����(A��PU�̋���)
��6�~(1/2)��{AP^2�|(PU/2)^2}
��3��(7^2�|3^2)
��3��(49�|9)
��3��40
��6��10 >>867�������܂��BR����Ȃ���U�ł����BP�AQ�AR�AS�����ꂼ��TB�ABC�ACU�AUT�̒��_�ƂȂ�悤�Ɏl�p�`TBCU��܂莆�ƌ����ĂĐ����`�̕ӂŐ܂�Ԃ��܂��B�߂����������܂�Ƃ��̊����ł��B��ATU�����[�Ȃ킯�ł��B�O>>868(U��R���߂����ēǂ݂܂�����)
��APU�����PU�~(1/2)�~����(A��PU�̋���)
��6�~(1/2)��{AP^2�|(PU/2)^2}
��3��(7^2�|3^2)
��3��(49�|9)
��3��40
��6��10 >>862
����ܗ����o���ĂȂ����ǁA��蕶�I�ɂ́u50�l�̒���A����Ɠ����a�����̊m���v���Ė�Ȃ���ł���H
�u50�l�̒��œ����a�����̊m���v���Ęb�ł���H
���O�̂�����ƗႦ��B�����E���a�����������������ꍇ�������Ȃ����H >>870
���肪�Ƃ��B
���̋^����āA���܂���50�l�̒�����m�������߂�̂ƁA�����̕ꐔ�̒����疈�x
�s�b�N�A�b�v�����ꍇ�̈Ⴂ���Ǝv���̂ł����A���ꂾ�����Ƃ����疳���̕ꐔ�̒�����
�I�����a�����̏d���Ƃ����Ӗ��ł͒Ⴍ�Ȃ�Ǝv���̂ł����A�v�Z���ʂ��t��
�Ȃ��Ă��܂����Ƃ��s�v�c�Ȃ̂ł��B
�����̕ꐔ�̒�����ЂƂs�b�N�A�b�v���āA�����悤�Ƀs�b�N�A�b�v���ĘA��22��
�Ⴄ�a�������������Ă�m�����i364/365�j^22=94.1% �B
�����22�s���āA�a�����������l�����Ȃ��m����94.1��^22�B=26.5�� ������A
�����a����������m����73.5���ƂȂ��āA(1/365*1/364*�c..1/343)��50.7%��ꡂ���
�����Ă��܂��̂ł��B ���܂����B���̂܂ɂ�23�l�Ōv�Z���Ă����I
>>869
����ς�PU=6�̗��R���킩��܂���
PBQ��PUQ�͍����ɂ͂Ȃ�Ȃ��Ǝv���̂ł��� >>871
�܂��Ȃ��22��(50��H)���s�����́H
22��A���Ⴄ�a�������������Ă�m������22����������ăX�b�Q�[�Ӗ��Ȃ��Ǝv�����ǁB
�����(364/365)^22�ł�����͍ŏ��̐l�ƒa�������Ⴄ�m���ł����đS�Ă̐l�̒a�������Ⴄ�m���ɂ͂Ȃ�Ȃ� >>873���Ȃ����܂��B�O�ɐ܂莆�Ɍ����Ăĉ������L��������܂�������ŁB
�O>>869
������ƍ��A�Ă�48���ԗ␅(�̂��ʂ�ܓ�)�ɐZ���Ă��܂��܂��āA���������肪��������Ń��L���V���l���Ă܂��B >>858�̏������݂���B���͂���őS�����H���ĂЂƂ��������ĂȂ����B 4+2+2+2(+1��22��)
��4�~2�~2�~2(�~1��22��)
���B��̉��ł��ȁB
(1)
(2)[24],6,6.
(3)
(4)[22],2,2,2,4.
���̖��ɑ��鎄�̓����̊ԈႢ���w�E���Ē����܂��H
<���>
n�̔�������B���ꂼ��̔��ɂ�1〜n�̔ԍ����U���Ă���B
m�im<n�j�̃{�[����ׂɔ��ɓ��ꂽ���A2�ȏ�̃{�[���������Ă��锠�����Ȃ��Ƃ�1����m�������߂�B
�������A���x�ł��������Ƀ{�[�������ėǂ��B
<����>
�i�܂���x���Փ˂��N���Ă��Ȃ��Ƃ��j
1�Ԃɔ��ɓ���{�[�����Փ˂���m����0/n
2�Ԃɔ��ɓ���{�[�����Փ˂���m����1/n
m�Ԃɔ��ɓ���{�[�����Փ˂���m����(m-1)/n
����ďՓ˂�1�x�ł��N����m����
(0+1+�c+(m-2)+(m-1)) / n = m(m-1)/2n
>>803
>>805
���肪�Ƃ��������܂��I ���Q���A���S���A��S���A�n�S���A���S���A�p�Q���A��Q���A���P�O���̍��v�R�Q�����~�ɕ��ׂāA4�l�ŏ��Ԃɔ����v���ɂP�����Ƃ��Ă����B
���̂Ƃ��A
(1)�W���̔z�v���ׂĕ��ɂȂ�m��
(2)���̂���2�l���T�������������Ă���m��
�����ꂼ�ꋁ�߂�
>>883
P(1��ڂɏՓ˂���)
�{P(1��ڂ܂ł͏Փ˂���2��ڂɏՓ˂���)
�{P(2��ڂ܂łɏՓ˂���3��ڂɏՓ˂���)
�{�c
�Ƃ��Ȃ��ƃ_�� ���w�҂ƕ����m�͂ǂ����̕��������ł����H
�ǂ������H�̐����ɂ͏��ĂȂ��Ƃ����Ӗ��ŁA�����ł��B
>>884
(1)P(�N������10��) = 4�~10/32*9/31*�c*1/23
(2)P(�����ꂩ�Q�l�����T������) = 6�~C[10,5]�~C[10.5]�~10/32�~�c�~1/23 >>886
�ւււււււււււււււււււււււււււււււււււ� >>865
�����Đς�P���ē��ꂽ�猋�������藧���Ȃ��悤�ɂ��ł���������� ��������>>840�̐}�`���Ăق�Ƃɑ��݂���́H ���炵�܂����B>>840�̐}�`���݂��܂��ˁB�悭����Ȑ}�`�����ė����Ȃ��B >>840
P�AQ�AR�AS�����ꂼ��TB�ABC�ACU�AUT�̒��_�ƂȂ�悤�Ɏl�p�`TBCU��܂莆�ƌ����ĂĐ����`�̕ӂŐ܂�Ԃ��܂��BTBCU�̎l�̒��_���A�����`PQRS���̈�_V�ɏW�܂�B
�O>>875
PQRS��(1/2)(��ABC�|��ATU)
��APR/��ATU��(1/2)AP�ARsin�`/(1/2)AT�AUsin�`��9
�l�p�`TPRU/��ATU��8
�l�p�`PBCR/��ATU��8
�l�p�`PQRS/��ATU
��(1/2)(�l�p�`TBCU/��ATU)
��(1/2)16
��8
TP��PB��PV��6�AUR��RC��RV��2�ATS��SU��SV�ABQ��QC��QV
SQ��PR��8
��PQRS��(8^2)/2��32
PQ��QR��RS��SP��4��2
��5.656854
�ǂ��ł����H >>893
�������Ȃ���
�����Ă݂���{���Ɉ�_�ɂȂ��� >>894���X���肪�Ƃ��B
�����Ă邩�킩��Ȃ����ǂȂ�ׂ����m�Ȑ}�������ċ߂�������T�����B
�Ȃɂ���ĂA���Ďv���C�ɂȂ��Ă܂��l���Ă��܂��B�Ȃɂ���������@������͂��A�Ǝv���Đ}�������Ă��܂��B
�O>>893��ꂽ�B >>893
�l�p�`TPRU���l�p�`PBCR �ƂȂ��Ă�͉̂��ŁH ���̖�肪������܂���
an=(1+1)(1+1/2)(1+1/3)�E�c�E(1+1/2n)
bn=(1+1)(1-1/2)(1+1/3)�E�c�E(1-1/2n)
�̂Ƃ��An�����Ƃ����Ƃ���an��bn�̋Ɍ��ׂ�B
an�͖����傾�Ǝv���̂ł����Alog������肵�Ă�������������܂���
bn�̕��͑S��������Ȃ��ł�
��낵�����˂������܂�
>>897
�Ƃ肠�����C�ɂȂ�����
{1+1}{1+(1/2)}{1+(1/3)}��c�c�{1/2n}
�ĂȂ�������
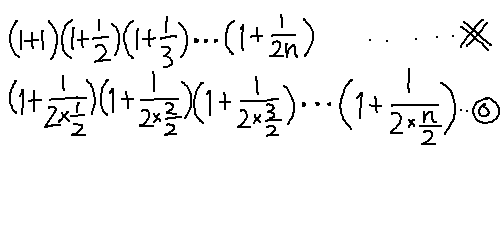
>>893
��H���Ǔ���(27.5)�Ƃ͈Ⴄ�̂ł́H >>897
an��bn��������n�̎��ŕ\���Ă݂�Ƃ��� �e ( ) �̒���ʕ����Ă��� an, bn �߂�ƁA
�킳�킳���Ɩł��邾��H
a_n=��[k=1,2n](1+1/k)=��[k=1,2n](k+1)/k=2n+1
lim[n����]a_n=��
b_n=��[k=1,2n](1+((-1)^(k-1))/k)=��[k=1,2n](k+((-1)^(k-1)))/k=(��[l=1,2n]l)/(��[m=1,2n]m)=1
lim[n����]b_n=1
>>899
>��H���Ǔ���(27.5)�Ƃ͈Ⴄ�̂ł́H
�����́A27.2����B136/5 = 27.5�H �Ō�Ƀ{�P�Ă�B >>893TU��BC�������Ɍ����܂����B�������܂��B
P�AQ�AR�AS�����ꂼ��TB�ABC�ACU�AUT�̒��_�ƂȂ�悤�Ɏl�p�`TBCU��܂莆�ƌ����ĂĐ����`�̕ӂŐ܂�Ԃ��܂��BTBCU�̎l�̒��_���A�����`PQRS���̈�_V�ɏW�܂�B
TP��PB��PV��6
BQ��QC��QV
UR��RC��RV��2
TS��SU��SV
�O>>896
PQRS��(1/2)(��ABC�|��ATU)
��APR/��ATU��(1/2)AP�ARsin�`/(1/2)AT�AUsin�`��9
�l�p�`TPRU/��ATU��8
��ABC/��ATU��13�11/7
��143/7
�l�p�`PBCR/��ATU��(143/7)�|9
��80/7
�l�p�`PQRS/��ATU
��(1/2)(�l�p�`TBCU/��ATU)
��(1/2)(8�{80/7)
��(1/2)(136/7)
��68/7
��ATU��(1/2)1�7sin�`
��(7/2)sin�`
PQRS��(68/7)(7/2)sin�`
��34sin�`
(��)
��ATU��(7/2)sin�`��2
�Ɨ\�z����B
PQRS��136/7
��19.428571 >>881
(2) [24], 6, 6.
(2) [24], 2, 26.
(3) [23], 2, 2, 9.
(4) [22], 2, 2, 2, 4. >>886
�ǂ������H�Ƃ����Ӗ��ŁA�����ł��B >>856
����L�������ł��邷�ׂĂ̒P���i�P���㐔�j�͍s��ŕ\���ł���B
J.�E�F�_�[�o�[��(1908)�AE.�A���e�B��(1927�j y��(100x-x^2)/1000�@0��x��100
��y�̍ő�l���Ăǂ�����ċ��߂��炢����ł����H
�������Ɖ����Ă��������B
���̍ő�l�͗B��i�G���A�����_�E�@�X�P���g�t�������I�v�@1940 Vol1 p1�j
�����p�`K�̊O�ډ~�̔��a��1�̂Ƃ��AK�̓��ډ~�̔��ar��r>0.87�ł��邱�Ƃ������B
�O>>905�O�X895�O�ɉ��������Ƃ�����悤�ȋC������BBC��TU���������A��_��W�Ƃ���ƁA���l���E�X�̒藝����ATS:SU:UW��10:10:13
BQ:QC:CW��10:10:1
�܂�Ԃ����l�_��V�ɏW�܂�Ƃ��āAPV��6�ARV��2����l���āARV��5�ASV��2.5���炢����Ȃ����ƁB
�Ίp����7���炢�Ȃ�PQRS��24.5���炢�����肤��B
�^�P�P�P�P�P�P�P/�_
[�P�P���� �����P�_/|
[�Q�i(-_-)-_-))�@/ |
�P|`(��u~)U��U��^| |
�n| �a�҃�~UU~�a |/|
�Q| �a ���@�� �a / |
�P|`�a�Q�Q�Q�Q�a/| |
�n| �a�P�P�P�P�a |/ �_
�Q| �a ���@�� �a /�@ /
�P�_�a�Q�Q�Q�Q�a/�@ /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�P�P�a�@|
���@���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^|
�Q�Q�Q�Q�Q�Q�Q�Q�a�^_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q��_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/(�Â�) >>909�ʓ|������W�����������
y=(100x-x^2)
dy/dx=100-2x
��ɓʂ̊�������x=50�̎��ő�l�����
���Ƃ�(100x-x^2)/1000��x=50����
(5000-2500)/1000=5/2 TS:SU:UW��10/3:10/3:13/3
BQ:QC:CW��5:5:1/2
���̕ӂ�B
�O>>913���5.25�Ȃ�A
PQRS��27.5625 �{���ɂ��������E�E�E�E�E�B
���ɂȂ��Ă�����x�ƗL�ɂȂ肽���Ȃ��E�E�E�E�E�B
���E���Ă����ʂ��ȁH
>>840
���w���Ă���Ȃ���Ȃ̂��H
�ȉ������y�іʐς̒P�ʂ��ȗ�����
��PBQ��_P���S�Ŕ����v����90���A��QRC��_R���S�Ɏ��v����90����]������
����ABC-��PQRS=(7�~6+9�~2)/2=30��
����PQR:��ABC
=1-{(7/13)(9/11)+(1/2)(6/13)+(1/2)(2/11)}
=34:143
����PQRS=30{(143-34)/68}=136/5 �����́B��y���B���͂����݂��������B
c1c2=c1+c2���
c2�����߂Ȃ����B
��������������܂���B�D����������Ղ����������肢���܂��B
>>919
�������傢�������t���Ă�͂������炻��������āB
c1�Ac2�͐������Ƃ�����Ȋ����̂�B 919�ł�
�R�����g���肪�Ƃ��������܂��B
C��X�ɕς��Ă����v�ł��B�����ł��B
���萔�ł�����낵�����肢���܂�
>>919
c1c2=c1+c2
c1c2-c2=c1
(c1-1)c2=c1
c2=c1/(c1-1) ������ c1��1 ���肪�Ƃ��������܂��I�I
3�s�ڂ�-1�͂ǂ�����o�Ă�����ł��傤���B��{�I�Ȏ��Ő\�������܂����B
�A�������܂���
>>912
���߂锼�a�� r = cos(��/7)
(1)
sin(��/7) < ��/7,
r = cos(��/7) > ��{1 - (��/7)^2} = ��(39) /7 > 6.23 / 7 = 0.89
(2)
sin(��/14) < ��/14,
r = cos(��/7) = 1 - 2{sin(��/14)}^2 > 1 - (1/2)(��/7)^2 > 1 - 5/49 = 0.897959 >>924
�u���z���v�����ȏ��Ŋm�F����B >>923�l
���肪�Ƃ��������܂����B
�g���C�C�b�g�̓�������x���Ă���������ɐi�߂܂���ł����B
�{���ɏ�����܂����B���炵�܂����B ���z���I�m�F���܂��I
������܂����I
>>918���肪�Ƃ��������܂��B���̂܂܂Ȃ����������ꂸ�ɏI��邩�Ǝv���܂����B��ABC�|PQRS��30�Ɓ�ABC:PQRS��143:68 ��}�������Ċm�F(sin�`�͖�)���A�����Ȃ�ɗ����������������B
�a�P�P�a�P�P �^���_�P/
�a�����a����(�L�́�)��
�i�@(`)(^o^))��~����
�i��[�P]����)�@���@)��
�u�P�P�P�P�P]`�҃ҁP��
��/_UU_�QUU����a�^�_���Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q�O>>916
����30c�u�ɂ��āA��ABC����PQRS�������������ɑ���PQRS�̊�����������B
PQRS��30�~PQRS/(��ABC�|PQRS)
��30�~34�~2/(143�|34�~2)
��30�~68/75
��27.2(c�u) �O>>929
�O�p�`���O����180����]�����肵�Ă܂����B
�����Ɋi�[����90���������Ƃ́\�\�B >>924
���z�����g���Ƃ��ɁAc2��1�~c2�ƍl����Ƃ������Ƃł��B ��`T�ɓ��ڂ���~C������B�ȉ��̖���̐^�U�Ƃ��̗��R���q�ׂ�B
�i1�jT��2�{�̑Ίp����C�̒��S��ʂ�Ȃ�AT�͐����`�ł���B
�i2�jT�̑Ίp���̂�������1��C�̒��S��ʂ�A���AT��1�̓��p��90���ł���AT�͐����`�ł���B
>>933
(1)�U�F�����`�łȂ��Ђ��`������B
(2)�^�F�O���������������邱�Ƃ͂Ȃ��B �ȉ��̏�������xy���ʏ�̋Ȑ��̗�Ƃ��̎���^����B
�E0<x<1�ɂ����ď�ɁA���~(x-1)^2+y^2=1�iy≥0�j�Ɣ��~(x-1/2)^2+y^2=1/4�iy≥0�j�̊Ԃɂ���
�E�Ȑ��̑S���͖�����ł���
�E(0,0)��ʂ�
�Ȃ�a�̒��_�����b�ɕ��s�ɕ�c�ɐ����Ђ��ē����悤��b�̒��_����c���ĉ��������a+b��c�ɂȂ���Ă����藝��m���Ă���A���O�������Ă�������
���̑���ŏo����O�p�`�͌��̎O�p�`�Ƒ����ŁA�Ή�����ӂ̒����͔����ɂȂ��Ă����̂łǂ�ǂ����Ȃ���a+b��c�ɂȂ��Ă����܂�
��Ԃ�xy���ʏ�ɉ~��C:x^2+y^2��1,z=0������B
C��ɓ_P(px,py,0)���Ƃ�AP��ʂ�xy���ʏ�̒���l���l���Al��C�Ƃ̌�_��A,B�Ƃ����B�܂��A��PA�EPB�̒l��pz�Ƃ���B������P��C�̎���ɂ���Ƃ��Apz=0�ł���B
C���P�������Ƃ��A�~��C�ƁA�_(px,py,pz)�S�̂̍��ȖʂƂɂ��͂܂��̈�̑̐ς����߂�B
>>936
�@���������~�� y = g(x)�C�傫�����~�� y = G(x) �Ƃ��āA�ꉿ��
�@f(x) = {G(x)+g(x)}/2 + {G(x)-g(x)}/2�Esin(��/(1-x))
�@x��1 �̂Ƃ��A1�������邲�Ƃɖ�2�����L�т�
*)�@g(x) = ��{x(1-x)}�Ah(x) = ��{x(2-x)} >>912
(3)
��/7 < 7��/48 = (��/6 + ��/8)/2,
r = cos(��/7) > cos((��/6 + ��/8)/2)
�@> {cos(��/6) + cos(��/8)} /2�@�@(����ɓ�)
�@= {��3 + ��(2+��2)}/4
�@= 0.89495 >>941
G(x) = ��{x(2-x)},
>>936
�`���g�ύX
f(x) = ��{x [ h(x) - x] },
h(x) = {3 �} sin(��/(1-x))} /2, 1000��菬�������̂����A4�Ŋ����3�]��A����5�Ŋ����4�]�鐔�̌��͂������B
4��5�Ŋ����-1�]��ƍl��4,5�̍ŏ����{��-1��19������ɑ�������Ǝv��
1000/19��52���Ǝv�����̂ł���������50�炵���ł��c�c�Ȃ��ł��傤���c�c
>>944
4�Ŋ����3�]�肩��5�Ŋ����4�]�鐔�A�Ƃ����̂́u20�Ŋ����19�]�鐔�v�̂��Ƃł����āA19�̔{���ł͂Ȃ�����ł� �~�����̍Ō�̐�����x�Ƃ���x-1���߂��1������x�����܂�܂���ˁH�����x��3�ł����Ă܂����H
�������Đ��w�S���o�����ɘQ�l���Ă��܂����K�C�W�ɂ��D���������Ă�����H�ł���Ύ��ɏ����ē\���Ăق����B
>>912
(4)
cos�� = x�@�Ƃ���ƁA
cos(4��) + cos(3��)
= (8x^4 -8x^2 +1) + (4x^3 -3x)
= (x+1)(8x^3 -4x^2 -4x +1)
= (x+1) f(x)
f '(x) = 4(6x^2 -2x -1)
�@x = (1-��7)/6 �ɋɑ�l (7/27)(1+2��7)
�@x = (1+��7)/6 �ɋɏ��l (7/27)(1-2��7) ������A������E�ł͒P������
�@f(0.9) = -0.008 < 0 = f(cos(��/7)) = f(r),
���@0.9 < r �f���̊Ԋu�ɍő�l�������Ƃ̂��Ƃł����A�ł́A�f��A�Ǝ��̑f��B�̊Ԋu���f��A�̐��ȏ�ɂȂ�f���̑g�ݍ��킹�͑��݂����܂����H
������ؖ�����藝�݂����Ȃ��̂�v�Z���@�A���������I�Ȃ��̂͂���܂����H
������G�c�Ȋ��o���Ƒ��݂��Ȃ��悤�Ɏv���̂ł���
����Ȃ��Ƃ��l�����l�������肵�܂����H
�̌n���w�̂��̖�肪�킩��܂���
������������
��1����200�܂ł̎��R���̂����A3�Ŋ�����1�]�鐔�̘a�����߂�
���ɖ��Ȃ͍̂�����66�ɂ����Ȃ�Ȃ����Ƃł�
>>953
A��2A�̊Ԃɂ͕K���f�������� >>955
��������̘a�́A�����Ɩ����𑫂��č������|�������̂��Q�Ŋ���
��`�̖ʐς̌����ƈꏏ�Ɋo����ƖY��Ȃ� >>955
67����܂����
���̖{���Ԉ���Ă��Ȃ��ł����H >>957
>>958
�ԐM���肪�Ƃ��������܂��B
���͎����킩��Ȃ��̂͂ǂ����č�����67�ɂȂ邩�Ȃ�ł�
���W�̉�67�ł�
66�͎��̌v�Z�ł�
�����I�ł��݂܂������Ă������� >>959
1,4,...,199
1+3�~0,1+3�~1,...,1+3�~66
1����66�܂ł�66����܂�����A0����66�Ȃ�67�ł��� ( 199 - 1) / 3 = 66 ������
���B���ƃ}�L�V���E�R���c�F�r�b�`�͂ǂ����̕����V�˂ł����H
>>959
>>961�̐����ŏ[�������A�ڂ����m�肽����u�A�؎Z�v�ɂ��Ē��ׂĂ݂悤 ���f�����ʏ�̒P�ʉ~C���_P(z)�������Ƃ��A�_Q(z^3-z)�̋O�Ղ�}������B
�Ɍ�
lim[n����] {��n}{(2n,n)/(4^n)}
�����߂�B
������(k,m)�œW��kCm��\���B
>>966
z = e^(it) �Ƃ����B(0��t<2��)
z^3 - z = (z - 1/z) zz
�@= {e^(it) - e^(-it)} e^(2it)
�@= 2sin(t)�Ee^(i(2t+��/2))
�@= r�Ee^(i��)
�ɍ��W�ł�
�@r =�b2sin(t)�b=�b2sin{(��-��/2)/2} |,
�f�J���g���W�ł�
�@(xx+yy)(2-xx-yy)^2 - (2y)^2 = 0,
���t���kn=1/2�l
�u���w����I�v ��g�S��221 (1956)�@p.286-297 �̑�6.95�}�A��6.97�} �𗧂Ă��`�B >>959
1 ����@100�@�܂Ő����͉�����܂����H
100-1=99�ł��A
�̃��x�� >>967
sin �̖�����ϕ\���i�I�C���[�j
�@sin(x) = x ��[k=1�C��] {1 - (x/k��)^2}
�� x=��/2 �Ƃ�����
�@1 = (��/2) lim[n����] ��[k=1�Cn] {1 - (1/2k)^2}
�@�@= (��/2) lim[n����] ��[k=1�Cn] (2k+1)(2k-1)/(4kk)
�@�@= (��/2) {lim[n����] (2n+1)!! (2n-1)!!/(4^n)(n!)^2 }
�@�@= (��/2) {lim[n����] (2n+1) [(2n-1)!!/(2^n�En!)]^2 }
(2n�Cn) = (2n)! / (n!)^2 = (2^n)(2n-1)!! / n!
��(2n+1)�E(2n�Cn) / 4^n = ��(2n+1) [(2n-1)!!/(2^n�En!)] �� ��(2/��),�@�@�@(n����)
��n�E(2n�Cn) / 4^n �� 1/���,�@�@(n����)
�X�^�[�����O�̌������g���Ă��悢�B �������ď������x���̖��`���Ă������H
>>970
�@(2�2)/(1�3)�~(4�4)/(3�5)�~(6�6)/(5�7)�c�c
�@= ��[k=1�C��] (4kk) / {(2k+1)(2k-1)}
�@= lim[n����] (4^n)(n!)^2 / {(2n+1)!!(2n-1)!!}
�@= ��/2,
���E�H���X�ρi�E�H���X�̌����j�Ƃ����炵���B �Q�����𗧂Ă����̂ł����Ȃ��Ȃ���肭���܂���B�����ĉ��������肢���܂��B

>>959
�����������������l���������ꍇ�A
�����鐔�����܂�ɂȂ�܂��B
1��3�̏ꍇ�A�����鐔1���]��ɂȂ�܂�
�܂�A200��3��66�̂ق��ɁA1��3�Ŋ���Ɨ]�肪1�ɂȂ鐔�ɂȂ�܂�
����āA�S����67���邱�ƂɂȂ�܂� �����܂���
np^n=p^n+1
����p��������������
���̖��������Ă�������

�����ʑ�V�̊O�ڋ�B��ɓ_P���Ƃ�AP��V�̊e���_�Ƃ�����6�{�̐��������B
����6�{�̐������̘a���ő�ɂȂ�悤��P�̈ʒu��1���߂�B
>>982
�O�ڋ��͌��_���S�A���a1�Ƃ��A�e���_�͎���Ƃ��Ă悢�B���_P(��x,��y,��z) (x+y+z=1)�Ƃ��Ă悢�B
f(t)=��(1+��(1+x))+ ��(1-��(1+x))
�Ƃ�����
�����̘a=��2(f(x)+f(y)+f(z))�ł���Af�͏�ɓʂ����璷���̘a���ő�ƂȂ�̂�x=y=z=1/3�̂Ƃ� k�����R���Ƃ��A
S(n,k)=�[i=1��n] i^k
�ƒ�߂�B
S(n,k)��S(n,m)�im=0,1,2,...,k-1�j�̂����K�v�Ȃ��̂�p���ĕ\���B
>>976
���Ă��ɉ�����̂ł���
>>all
67�Ԃ̖�肪�����̂������Ԉ���Ă邹���������������܂���B�����̂�����2���ڂ̉摜�̂悤�ɂ���Ă���̂ł����A�ǂ����Ⴄ�̂����킩��܂���B���Ȃ݂ɓ����͐��Z�p�`�̈�ӂ�x�ƒu���Ă���Ă��܂��B
�l�͐j���̒�����x��30-x�ɕ����Ă���Ă��܂��B
���Â炭�Đ\����Ȃ��ł��A�����Ȃ�����������Ό����Ă���������Ε⑫���܂��B


717�Ɋ֘A���ā@�ł���
���i���j�� ax^n + bx^(n-1) + cx^(n-2) + dx^(n-2) + �E�E�E + e�Ƃ���.�C�u�����W���́vn�����������ɂ���
��_[0,1] { f(x) }^2 dx ���l����Ƃ��A�����
�@a = 1, b = -1. c = d =�c= e = 0
�̂Ƃ��ɍŏ��ƂȂ�
�Ƃ�����ł��傤���B
>>988
����߂Ē��ϓI�ł���
�@f(0) = f(1) = 0
�܂�
�@f(x) = x(x-1)g(x)
�̌`���ǂ��A����
�@f(x) = x^k (x-1)^(n-k)
�� k �� n-k ���傫���in/2 �ɋ߂��j���̂��ǂ����B
�������A�����Njy���Ă��u�G���K���g�ȉv�ɂ͂Ȃ���K�X^^
>>720 �͎��W���̏ꍇ�H ���܂�A�����W���������Ɗ��Ⴂ���Ă��B
�ł� >>988 �͌��B
���� ��[0,1](x^4 - 2 x^3 + x^2)^2dx=1/630 < ��[0,1](x^4 - x^3)^2dx=1/252 >>991 �̗�� n=4�Cf(x) = x^2 (x-1)^2 �ł���^^ ���肪���������܂�
���̘H���ł����Ă݂܂���
���鋉��{an}�̕����a�̍�閳�������{Sn}�Ƃ���B
�����a{Sn}���������āA���̋Ɍ��l��S�ł��鎞�A
����{an}�̘a��S�ɓ������B
�Ȃ�łł����H
>>990 �̗���ŏ��ɂ͂Ȃ�Ȃ��悤�ł��B
���� ��((x-1)^2 (2x-1)^2 x^2)^2dx=1/30030 < ��((x-1)^3 x^3)^2dx=1/12012 >>996
�Ȃ�ł��������Ⴊ�����Ɏv�����̂ł���
�ǂ�ȕ��Ɍ����Ă���������̂ł��傤�� >>998
�ނ����A���������_���Ƃ�������i16���j lud20220919143032ca
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1522418128/�q���g�F5ch�X����url��
http://xxxx.5ch
b.net/xxxx �̂悤��
b�����邾���ł����ŃX���ۑ��A�{���ł��܂��B
TOP�� TOP�� �@
�S�f���ꗗ ���̌f���� �l�C�X�� |
>50
>100
>200
>300
>500
>1000��
�V���摜
�@���u������Ȃ����͂����ɏ����Ă�442 YouTube����>1�{ ->�摜>31�� �v�������l�����Ă��܂��F
�E������Ȃ����͂����ɏ����Ă�422
�E������Ȃ����͂����ɏ����Ă�432
�E������Ȃ����͂����ɏ����Ă�452
�E������Ȃ����͂����ɏ����Ă�428
�E������Ȃ����͂����ɏ����Ă�438
�E������Ȃ����͂����ɏ����Ă�447
�E������Ȃ����͂����ɏ����Ă�416
�E������Ȃ����͂����ɏ����Ă�445
�E������Ȃ����͂����ɏ����Ă�454
�E������Ȃ����͂����ɏ����Ă�453
�E������Ȃ����͂����ɏ����Ă�420
�E������Ȃ����͂����ɏ����Ă�433
�E������Ȃ����͂����ɏ����Ă�441
�E������Ȃ����͂����ɏ����Ă�449
�E������Ȃ����͂����ɏ����Ă�437
�E������Ȃ����͂����ɏ����Ă�455
�E������Ȃ����͂����ɏ����Ă�424
�E������Ȃ����͂����ɏ����Ă�436
�E������Ȃ����͂����ɏ����Ă�427
�E������Ȃ����͂����ɏ����Ă�456
�E������Ȃ����͂����ɏ����Ă�444
�E������Ȃ����͂����ɏ����Ă�456
�E������Ȃ����͂����ɏ����Ă�448
�E������Ȃ����͂����ɏ����Ă�446
�E������Ȃ����͂����ɏ����Ă�440
�E������Ȃ����͂����ɏ����Ă�478
�E������Ȃ����͂����ɏ����Ă�419
�E������Ȃ����͂����ɏ����Ă�450
�E������Ȃ����͂����ɏ����Ă�443
�E������Ȃ����͂����ɏ����Ă�431
�E������Ȃ����͂����ɏ����Ă�435
�E������Ȃ����͂����ɏ����Ă�439
�E������Ȃ����͂����ɏ����Ă�434
�E������Ȃ����͂����ɏ����Ă�451
�E������Ȃ����͂����ɏ����Ă�430
�E������Ȃ����͂����ɏ����Ă�417
�E������Ȃ����͂����ɏ����Ă�418
�E������Ȃ����͂����ɏ����Ă�426
�E������Ȃ����͂����ɏ����Ă�462
�E������Ȃ����͂����ɏ����Ă�429
�E�����������͂����ɏ����Ă�2
�E������Ȃ����͂����ɏ����Ă�463
�E������Ȃ����͂����ɏ����Ă�423
�E������Ȃ����͂����ɏ����Ă�421
�E������Ȃ����͂����ɏ����Ă�415
�E������Ȃ����͂����ɏ����Ă�465
�E������Ȃ����͂����ɏ����Ă�458
�E������Ȃ����͂����ɏ����Ă�457
�E������Ȃ����͂����ɏ����Ă�425
�E������Ȃ����͂����ɏ����Ă�459
�E������Ȃ����͂����ɏ����Ă�460
�E������Ȃ����͂����ɏ����Ă�461
�E������Ȃ����͂����ɏ����Ă�464
�E������Ȃ����͂����ɏ����Ă� 472
�E������Ȃ����͂����ɏ����Ă�357
�E������Ȃ����͂����ɏ����Ă�388
�E������Ȃ����͂����ɏ����Ă�389
�E������Ȃ����͂����ɏ����Ă� 466
�E������Ȃ����͂����ɏ����Ă� 471
�E������Ȃ����͂����ɏ����Ă� 467
�E������Ȃ����͂����ɏ����Ă˂Q�P�P
�E������Ȃ����͂����ɏ����Ă� 470
�E������Ȃ����͂����ɏ����Ă� 469
23:24:14 up 13 days, 8:32, 0 users, load average: 8.74, 8.44, 8.29
in 0.075245141983032 sec
@0.075245141983032@0b7 on 120313
|